косой изгиб

,

где  проекции полного прогиба на главные оси. Эти ве личины можно определить методом начальных параметров. Начало координат поместим на левом конце балки в точке А.

Прогиб в плоскости x0z. Начальные параметры:

     кН.

Составим выражение прогибов f_x (z) с помощью универсального уравнения упругой линии балки:

.                                         (1)

Величину ₀ определим из условия, что при f_x (l) = 0. Под ставляя в выражение (1) z = l = 4 м, получим:

;

.

Окончательно выражение прогибов f_x (z) будет иметь вид:

.                                                               (2)

Для определения прогиба в середине пролета подставим z = 0,5l = 2 м в выражение (2):

кНм³.

Учитывая, что Е = 210⁸ кН/м² и I_y = 89110^8 м⁴, получаем:

.

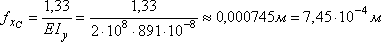Прогиб в плоскости y0z. Начальные параметры:

     кН.

Выражение для прогибов f_y (z) получаем с помощью метода на чальных параметров:

.                                                    (3)

Подставляя z = l = 4 м в выражение (3) и учитывая, что в т. В прогиб равен нулю, получаем уравнение для определения :

,

откуда

.

Окончательно выражение для прогибов f_y (z) будет иметь вид:

.                                                                 (4)

Для определения прогиба в середине пролета подставим z = 0,5 l = 2 м в выражение (4):

;

.

Определим величину модуля вектора полного прогиба

м.

Направление вектора полного прогиба показано на рис. 3. При этом, угол  определим по формуле:

;    .

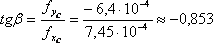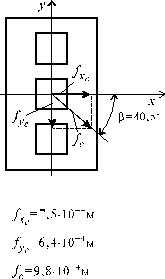
                                       Рис.3                                            

 

Пример 8.

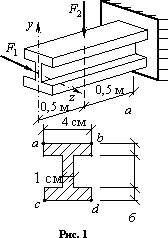
Для консольной двутавровой балки, загруженной горизонтальной силой F₁ = 0,56 кН и вертикальной силой F₂ = 5,84 кН (рис. 1), построить эпюру нормальных напряжений в защемлении и найти максимальное нормальноенапряжение .

Решение.

Нормальные напряжения определяем по формуле  Подсчитаем вначале величины изгибающих моментов в защемлении (по модулю):

M_y == 560 Hм;

M_z == 2920 Hм.

При этом момент M_z растягивает верхние волокна и сжимает нижние, а момент M_y растягивает левые волокна и сжимает правые.

Моменты инерции сечения, состоящего из прямоугольников, относительно осей  z и y равны:

I_z = 116,67  см⁴ =

 I_y = 29,5  см⁴ =.

Для построения эпюры нормальных напряжений вычисляем напряжения в угловых точках a, b, c, d (рис. 1, б). В точке а оба момента M_z и M_y вызывают растяжение, поэтому напряжение имеет величину:

      

В точке b момент M_z вызывает растяжение, а M_y  – сжатие, поэтому

В точке с момент M_z вызывает сжатие, а M_y  – растяжение, поэтому

В точке d оба момента M_z  и  M_y  вызывают сжатие, поэтому

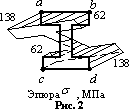
Определив напряжения в угловых точках и зная, что нормальные напряжения изменяются по закону плоскости, строим эпюру  (рис. 2). Из эпюры видно, что наибольшее нормальное напряжение  = 138 МПа.

 

Пример 9.

Для стальной балки, лежащей на двух опорах и нагруженной силой F = 60 кН, лежащей в плоскости zy и составляющей угол = 30^o с вертикальной осью y (рис. 1), подобрать прямоугольное сечение при условии, что h = 2b, R_y = 160 МПа,  = 1.

      

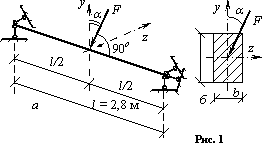
Решение.

Разложив силу на две составляющие по главным осям сечения балки, определим опорные реакции, действующие в главных плоскостях, и построим эпюры изгибающих моментов M_z и M_y, рис. 2, а.

Наибольшие моменты действуют в среднем сечении, где

В этом сечении наибольшие нормальные напряжения возникают в точках а (растяжение) и b (сжатие), рис. 2, б. Для них условие прочности запишется так:

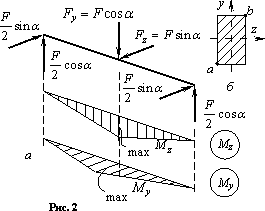
Вычисляем моменты сопротивления W_z и W_y при заданном соотношении высоты h и ширины b:

Подставляем в условие прочности значения M_z , M_y , W_z и W_y. В итоге получим

,

откуда 

 

 

Задачи для самостоятельного решения

Задача № 1

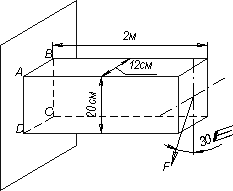
Деревянная балка длиной 2 м, имеющая прямоугольное поперечное сечение 12х20 см, защемлена одним концом и нагружена сосредоточенной силой F=2,4 кН на другом конце. Нагрузка лежит в плоскости поперечного сечения балки и проходит через его центр тяжести (см. рисунок). Построить эпюры нормальных напряжений по сторонам защемленного сечения и определить полный прогиб свободного конца балки.

Ответ: 

 

Задача № 2

Для балки, лежащей на двух опорах и загруженной тремя вертикальными сосредоточенными силами F₁ = F₃ = 10 кН, F₂ = 20 кН и равномерно распределенной горизонтальной нагрузкой q = 24 кН/м, требуется подобрать прямоугольное поперечное сечение с отношением  сторон h = 1,5b. Пролет балки равен 1 м, R_y = 150 МПа,  = 1 (см. рис.).

      

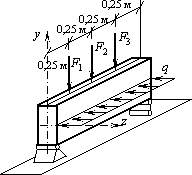
Ответ: b = 6 см, h = 9 см.       

 

Задача № 3

Балка прямоугольного поперечного сечения b×h = 0,18м×0,24м нагружена так, как показано на рисунке. Найти наибольшее нормальное напряжение, если сила F = 60 кН, пролет балки l = 3 м, угол между линией действия силы Fи вертикальной осью  = 30^o.

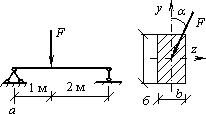
Ответ:  = 35,5 МПа.

 

Задача № 4

Определить наибольшие (по абсолютной величине) нормальные напряжения в балке пролетом 2 м, опирающейся на шарнирные подвижную и неподвижную опоры и несущую посередине пролета сосредоточенный груз F = 6кН. Сечение балки с прямоугольным отверстием показано на рис. 1.

У к а з а н и е Вначале необходимо определить положение нейтральной оси.

Балка прямоугольного сечения изгибается моментом М = 10 кНм (рис. 2). Найти точки с наибольшими нормальными напряжениями и вычислить эти напряжения.

Балка двутаврового сечения № 20 свободно опирается на прогоны, наклоненные под углом 30^о к горизонтали (рис. 3). Расстояние между осями прогонов 4 м. Балка посередине нагружена вертикальной сосредоточенной силой F = 8 кН. Пренебрегая собственным весом балки, определить напряжения в точках a, b, c, d и угол наклона  нейтральной оси сечения балки к главной оси z.

      

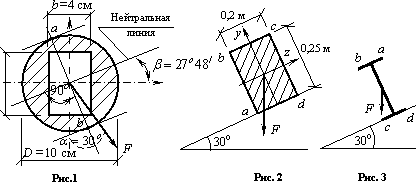
Ответ к рис.1: = 35,1 МПа.

Ответ к рис.2:  7,15 МПа;   –7,15 МПа.

Ответ к рис.3:  –210,9 МПа;  –135,5 МПа; 210,9 МПа;  135,5 МПа;   = 83^о48^/.

      

Задача № 5

Стальная консольная балка двутаврового поперечного сечения длиной l = 2 м изгибается силой F = 8 кН, приложенной к ее свободному концу (см. рис.). Пренебрегая собственным весом балки, подобрать номер двутаврового профиля и определить прогиб свободного конца, если = 30^o, R_y = 140 МПа, = 1 и модуль упругости Е = 2 МПа.

У к а з а н и е. Для двутаврового сечения при предварительном подборе принимают W_y / W_z = 8–10.

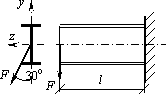
Ответ: двутавр № 36; прогиб w = 1,03 см.

 

Задача № 6

Стальная консольная балка двутаврового поперечного сечения (двутавр № 24) длиной 1 м загружена сосредоточенной вертикальной силой F = 40 кН. Найти максимальное нормальное напряжение в балке и вычислить прогиб конца консоли, если модуль упругости Е =МПа. Определить, как изменятся напряжения и прогиб балки, если сила F отклонится от вертикали на угол = 5^о.

Ответ: при прямом изгибе  = 138,5 МПа; w = 0,193 см; при косом изгибе напряжения и прогиб возрастают в 1,7 раза.

 

Задача № 7

При установлении опоры двутавра № 60 была допущена ошибка и стенка двутавра отклонилась от вертикали на угол равный 1^о. Определить связанное с этим увеличение нормальных напряжений и полного прогиба двутавра.

Ответ: напряжения увеличились на 20%, полный прогиб на 30%.

 

Задача № 8

Балка квадратного сечения, защемлена одним концом, на свободном конце нагружена силой F. В первом случае сила направлена параллельно стороне квадрата, а во втором  совпадает с его диагональю. Как изменится величина силы F  при переходе от  первого варианта ко второму при условии, что наибольшие нормальные напряжения в обоих случаях одинаковы.