Динамика твердого тела Дифференциальные уравнения движения твердого тела

Эти уравнения можно получить из общих теорем динамики механической системы.

1. Уравнения поступательного движения тела — из теоремы о движении центра масс механической системы В проекциях на оси декартовых координат ;;.

2. Уравнение вращения твердого тела вокруг неподвижной оси - из теоремы об изменении кинетического момента механиче­ской системы относительно оси, например, относительно оси :

Так как кинетический момент L_z твердого тела относитель­но оси , то если;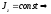

Так как или , то уравнение можно записать в виде или ,форма записи уравнения зависит от того, что следует определить в конкретной задаче.

Дифференциальные уравнения плоскопараллельного дви­жения твердого тела представляют собой совокупность уравне­ний поступательного движения плоской фигуры вместе с цен­тром масс и вращательного движения относительно оси, прохо­дящей через центр масс: ,,

Физический маятник

Физическим маятником называется твердое тело, вращаю­щееся вокруг горизонтальной оси, не проходящей через центр масс тела, и движущееся под действием силы тяжести.

Дифференциальное уравнение вращения .

В случае малых колебаний .

Тогда , где

Решение этого однородного урав­нения .

Пусть при t=0 Тогда

— уравнение гармонических колебаний.

Период колебаний маятника

Приведенная длина физического маятника — это длина та­кого математического маятника, период колебаний которого равен периоду колебанийфизического маятника.

Принцип даламбера

5.1. Силы инерции в динамике материальной точки и механической системы

Силой инерции материальной точки называется про­изведение массы точки на ее ускорение, взятое со знаком минус, т. е. Силы инерции в динамике применяются в следующих случаях:

1.При исследовании движения материальной точки в неинерциальной (подвижной) системе координат, т. е. относи­тельного движения. Это переносная и кориолисова силы инер­ции, которые часто называют эйлеровыми.

2. При решении задач динамики с использованием метода кинетостатики. В основу этого метода положен принцип Даламбера, в соответствии с которым вводятся силы инерции ма­териальной точки или системы материальных точек, движу­щихся с некоторым ускорением в инерциальной системе отсче­та. Эти силы инерции называются даламберовыми.

3. Даламберовы силы инерции применяются также при ре­шении задач динамики с использованием принципа Лагранжа-Даламбера или общего уравнения динамики .

Выражение в проекциях на оси декартовых координат

, ,,где - модули проекций ускорения точки на оси де­картовых координат.

При криволинейном движении точки силу инерции можно разложить на касательную и нормальную :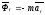; , , - модуль касательного и нормального ускорений;- радиус кривизны траектории;

V - скорость точки.

Принцип Даламбера для материальной точки

Если к несвободной материальной точке, движущейся под действием приложенных активных сил и сил реакций связей, приложить ее силу инерции, то в любой момент времени полученная система сил будет уравновешенной, т. е. геометрическая сумма указанных сил будет равна нулю.

, где - равнодействующая актив­ных сил, приложенных к точке; -равнодействующая реакций связей, наложенных на точку; сила инерции материальной точки. Примечание: На самом деле сила инерции материальной точки приложена не к самой точке, а к тому телу, которое со­общает ускорение данной точке.