Работа и мощность сил

Работа силы — скалярная мера действия силы.

1. Элементарная работа силы.

Элементарная работа силы — это бесконечно малая ска­лярная величина, равная скалярному произведению вектора силы на вектор бесконечного малого перемещения точки приложения силы: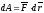 ; 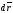- приращение ра­диуса-вектора 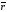точки приложе­ния силы, годографом которого является траектория этой точки. Элементарное перемещение 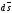точ­ки по траектории совпадает с 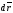в силу их малости. Поэтому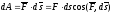

если 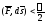тоdA > 0;если , тоdA = 0;если 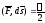, то dA < 0.

2. Аналитическое выражение элементарной работы.

Представим векторы и d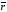 через их проекции на оси де­картовых координат:

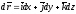, .Получим 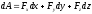(4.40)

3. Работа силы на конечном перемещении равна инте­гральной сумме элементарных работ на этом перемещении

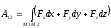
Если сила постоянная, а точка ее приложения перемещает­ся прямолинейно,

то

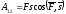
4. Работа силы тяжести. Используем формулу:F_x = F_y = 0; F_z = -G = -mg;

,

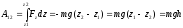где h- перемещение точки приложения силы по вертикали вниз (высота).

При перемещении точки приложения силы тяжести вверх A₁₂= -mgh (точка М₁ — внизу, M₂ — вверху).

Итак,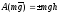. Работа силы тяжести не зависит от формы траектории. При движении по замкнутой траектории (M₂совпадает с М₁) работа равна нулю.

5. Работа силы упругости пружины.

Пружина растягивается только вдоль оси х :F_y = F_z = О, F_x = 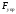= -сх;

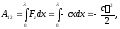где - величина деформации пружины.

При перемещении точки приложения силы 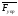из нижнего положения в верхнее направление силы и направление перемещения совпадают, тогда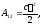

Поэтому работа силы упругости .

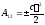Вращение тела вокруг неподвижной оси. Работа сил на конечном перемещении 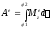; Если 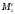=const, то,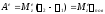

где 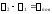- конечный угол поворота;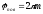, гдеп — число оборотов тела вокруг оси.

Кинетическая энергия материальной точки и механической системы. Теорема Кенига

Кинетическая энергия - скалярная мера механического движения.

Кинетическая энергия материальной точки - скалярная положительная величина, равная половине произведения массы точки на квадрат ее скорости,

т. е..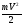

Кинетическая энергия механической системы — арифметическая сумма кинетических энергий всех материал точек этой системы:

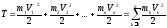
Кинетическая энергия системы, состоящей из п связанных между собой тел,

равна арифметической сумме кинетических энергий всех тел этой системы:

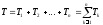
Теорема Кенига

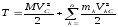Кинетическая энергия механической системы в общем случае ее движения равна сумме кинетической энергии движения системы вместе с центром масс и кинетической энергии системы при ее движении относительно центра масс: ,где Vkc — скорость k-й точки системы относительно центра масс.

Кинетическая энергия твердого тела при различном движении

Поступательное движение.

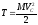
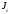Вращение тела вокруг неподвижной оси. ,где— момент инерции тела относительно оси вращения.

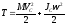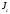3. Плоскопараллельное движение. ,где - момент инерции плоской фигуры относительно оси, проходящей через центр масс.

При плоском движении тела кинетическая энергия скла­дывается из кинетической энергии поступательного движения тела со скоростью центра масс 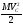и кинетической энергии вращательного движения вокруг оси, проходящей через центр масс, ;

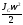Теорема об изменении кинетической энергии материальной точки

Теорема в дифференциальной форме.

Дифференциал от кинетической энергии материальной точ­ки равен элементарной работе силы, действующей на точку,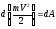

Теорема в интегральной (конечной) форме.

Изменение кинетической энергии материальной точки на некотором перемещении равно работе силы, действую­щей на точку, на том же перемещении.

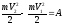
Теорема об изменении кинетической энергии механической системы

Теорема в дифференциальной форме.

Дифференциал от кинетической энергии механической системы равен сумме элементарных работ внешних и внут­ренних сил, действующих на систему.

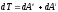
Теорема в интегральной {конечной) форме.

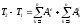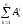Изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, приложенных к системе, на том же пере­мещении. ;Для системы твердых тел = 0 (по свойству внутренних сил). Тогда .

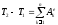Закон сохранения механической энергии материальной точки и механической системы

Если на материальную точку или механическую систему действуют только консервативные силы, то в любом поло­жении точки или системы сумма кинетической и потенци­альной энергий остается величиной постоянной.

Для материальной точки

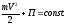
Для механической системы Т+ П= const

где Т+ П — полная механическая энергия системы.