
- •Плоское движение твердого тела
- •Уравнения плоского движения твердого тела
- •Мгновенный центр скоростей
- •Частные случаи определения мцс
- •Сложное движение точки
- •Теорема о сложении скоростей
- •Теорема о сложении ускорений (теорема Кориолиса)
- •Основные понятия классической механики
- •Динамика материальной точки
- •Две основные задачи динамики для материальной точки
- •Принцип относительности в классической механике
- •Моменты инерции твердого тела
- •Осевые моменты инерции некоторых однородных тел
- •1. Тонкое кольцо.
- •Центробежные моменты инерции
- •Общие теоремы динамики материальной точки и механической системы Теорема о движении центра масс системы
- •Работа и мощность сил
- •Кинетическая энергия материальной точки и механической системы. Теорема Кенига
- •Теорема Кенига
- •Динамика твердого тела Дифференциальные уравнения движения твердого тела
- •Физический маятник
- •Принцип даламбера
- •5.1. Силы инерции в динамике материальной точки и механической системы
- •Принцип Даламбера для материальной точки
- •Принцип Даламбера для механической системы
- •Главный вектор и главный момент сил инерции твердого тела
- •Введение в аналитическую механику Основные понятия аналитической механики
- •1. Связи и их классификация.
- •2. Возможные (виртуальные) и действительные перемещения.
- •Общее уравнение динамики (принцип Лагранжа-Даламбера)
- •Устойчивость положения равновесия механической системы
- •Явление удара. Ударная сила и ударный импульс
- •Теорема об изменении количества движения механической системы при ударе
Сложное движение точки
Сложным
движением называют
такое движение, при котором точка
одновременно участвует в двух или более
движениях
Абсолютным
движением
называют движение точки М
по
отношению к основной системе отсчета
O1X1Y1Z1,
которую
условно принимают за неподвижную.
Относительным движением называют
движение точки М
по
отношению к подвижной системе отсчета
OXYZ.
Переносным
движением
называют движение подвижной системы
отсчета OXYZ
относительно
основной (неподвижной) системы отсчета
O1X1Y1Z1.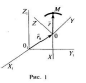
Теорема о сложении скоростей
Абсолютной
скоростью называют скорость точки М
относительно основной системы
координат O1X1Y1Z1
и
обозначают
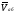
Относительной
скоростью называют скорость точки М
относительно
подвижной системы координат OXYZ
и обозначают
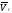
Переносной
скоростью называют скорость той точки
подвижной системы координат, с которой
в данный момент совпадает движущаяся
точка М,
и
обозначают
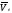
Абсолютная
скорость точки в сложном движении равна
геометрической сумме переносной и
относительной скоростей
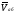 =
=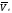 +
+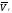
Модуль
абсолютной скорости в общем случае
находят проектированием выражения
на оси координат, так как угол между
векторами относительной и переносной
скоростей может быть от 0 до 180°:
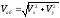
Теорема о сложении ускорений (теорема Кориолиса)
Абсолютное
ускорение точки в сложном движении
равно геометрической сумме переносного,
относительного и кориолисова ускорений:
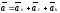
где
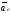 -ускорение
переносного движения;
-ускорение
переносного движения;
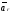 -
ускорение относительного движения;
-
ускорение относительного движения;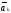 -
ускорение
Кориолиса:
-
ускорение
Кориолиса: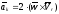
Направление ускорения Кориолиса определяют либо по правилу векторного произведения, либо по правилу Жуковского.
Правило Жуковского: проектируем вектор относительной скорости Vr на плоскость, перпендикулярную вектору переносной угловой скорости, и поворачиваем эту проекцию в той же плоскости на угол 90° в сторону переносной угловой скорости.
Модуль
ускорения Кориолиса:
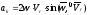
Равенство нулю ускорения Кориолиса возможно:
1. = 0; переносное движение является поступательным.
2. Vr = 0; относительная скорость в данный момент равна нулю.
3.
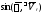 ;
вектор угловой скорости переносного
движения
параллелен вектору относительной
скорости Vr.
;
вектор угловой скорости переносного
движения
параллелен вектору относительной
скорости Vr.
При
вращательном переносном и криволинейным
относительным движениях выражение
примет вид
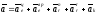 .
.
Модуль
абсолютного ускорения находим, проектируя
на выбранные оси координат: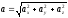 .
.
При
поступательном переносном и криволинейном
относительном движениях выражение
примет вид
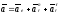 .
.
Основные понятия классической механики
Динамика — раздел теоретической механики, в котором изучается движение материальных тел (точек) пол действием приложенных сил.
Материальное тело — тело, имеющее массу.
Материальная точка — материальное тело, различие, в движении точек которого является несущественным.
Масса тела — это скалярная положительная величина, зависящая от количества вещества, содержащегося в данном теле, и определяющая его меру инертности при поступательном движении.
Сила - количественная мера механического взаимодействия между телами .
Сила — векторная величина, характеризующаяся величиной, точкой приложения и направлением (линией действия)
Динамика подразделяется на динамику материальной точки, динамику системы материальных точек (механическую систему) и динамику твердого тела.
