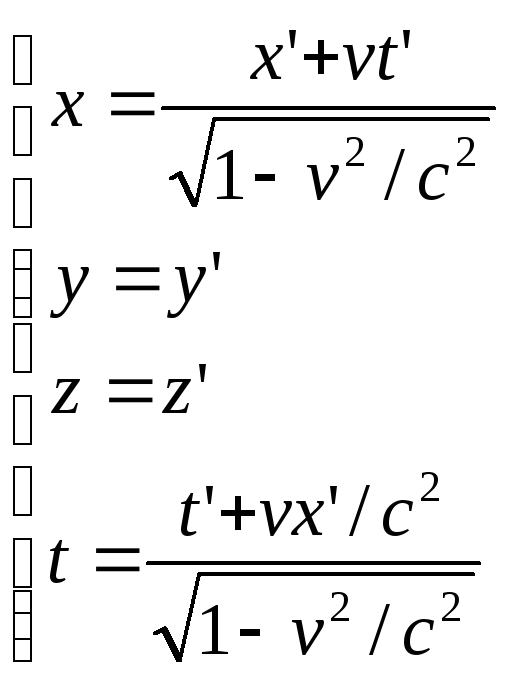shpory_po_fizike_main
.doc|
1. Физическая модель: При изучении реальных явлений мы встречаемся одновр. С большим разнообразием факторов, учесть некоторые из них мы можем, другие нет. По этой причине при решении любой реальной задачи мы вынуждены что-то отбрасывать, что-то упрощать. Т.е. моделировать. И таким образом мы приходим к понятию физической модели.(Например механика использует такие модели: материальная точка, система материальных точек, абсолютно твёрдое и абсолютно упругое тело, а также и абсолютно неупругое тело и мн.др.) После выбора физической модели, учёта всех факторов, выбирается математическая модель (т.е. просто формула) и далее производится расчёт задачи. Проблемы точности: Однако в физике существует проблема точности в вычислениях и измерениях. Различают измерения прямые и косвенные. Прямые получаем непосредственно из опытов, а косвенные измерения при которых мы всё определяем расчётным путём. Любые измерения сопровождаются ошибками (погрешности). Различают абсолютную (определяется как разность между истинным и измеренным значениями) и относительную (величина, равная отношению абсолютной погрешности к измеренному значению) погрешности. Погрешности же можно подразделить на случайные (случайным образом) , систематические (несовершенство разбивной шкалы,неточно указанный вес) и промахи (оч. большие ошибки, вызванные неправильными действиями экспериментатора.).
|
5. Центр масс системы материальных точек: Воображаемая точка С, положение которой характеризует распределение массы этой системы. Её
радиус-вектор равен: Закон движения центра масс: Центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил. Действующих на систему:
|
|
|
2.
Механическое
движение
– изменение
с течением времени взаимного
расположения тел или их частей. Виды:
равномерное, равноускоренное,
криволинейное и тд. Материальная
точка -
тело, размерами которого в данной
задаче можно пренебречь. Система
отсчёта
– совокупность тела отсчёта, связанной
с ним системы координат и синхронизированных
между собой часов. Средняя
скорость
– векторная величина, определяемая
отношением приращения радиуса-вектора
точки
Среднее
ускорение
– векторная величина, равная отношению
изменения скорости
|
6. Импульс материальной точки: векторная величина, численно равная произведению массы Материальной точки на её скорость и имеющая направление скорости. Замкнутая (изолированная) система: механическая система тел, на которую не действуют внешние силы. (механическая система: совокупность материальных точек (тел), рассматриваемых как единое целое. Внутренние силы: силы взаимодействия между материальными точками механической системы. Внешние силы: силы, с которыми на материальные точки механической системы действуют внешние тела. Закон сохранения импульса: импульс замкнутой системы сохраняется ( не изм с теч вр)
Это фундаментальный закон природы. Он является следствием однородности пространства: при параллельном переносе в пространстве замкнутой системы тел как единого целого её физические свойства не изменяются. Иными словами, не зависят от выбора положения начала координат инерциальной системы отсчёта. |
|
|
|
Нормальное
ускорение
характеризует быстроту изменения
скорости по
направлению
(направл.
к центру кривизны траектории), а
тангенциальное
характеризует быстроту изменения
скорости по
модулю
(направл. по касат. к траектории). ( Угловая
скорость
– векторная величина, определяемая
первой производной угла поворота
тела по времени.
Угловое
ускорение
– векторная величина, определяемая
первой производной угловой скорости
по времени. ( Связь между линейными и угловыми величинами: Тангенциальная
составляющая ускорения:
Нормальная
составляющая ускорения:
Связь
между линейными(длина пути S,
пройденного точкой по окружности
радиуса R,
линейная скорость V)
и угловыми величинами (угол поворота,
угловая скорость) выражается следующими
формулами:
Частота
вращения:
n
число полных оборотов, совершаемых
телом при равномерном его движении
по окружности, в единицу времени:
|
7. Движение тела с переменной массой В некоторых случаях в процессе движения масса тела изменяется. Например, движение ракеты, связанное с выбросом топлива, движение вагона при разгрузке щебенки.
До
начала движения импульс тела равен
Импульс
газа —
Согласно закону сохранения импульса:
В
том случае, если внешние силы равны
нулю, и начальную массу обозначить
через
интегрируя
это уравнение, получаем
Для
того чтобы ракета достигла первой
космической скорости при относительной
скорости v=1
км/с соотношение
|
|
|
4. Масса тела – физическая величина, являющаяся одной из основных характеристик материи, определяющая её инерционное(инертная масса) и гравитационные (грвитационная масса) свойства. Сила – величина векторная, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. Законы Ньютона: 1-й: Матер. точка (тело) сохраняет состояние покоя или равномерного движения до тех пор, пока воздействие со стороны др тел не заставит её изменить это состояние.(Существ такие сист отсчёта, относ которых поступательно движущ тело сохр свою скорость постоянной, если на них не действуют другие тела. (1-й зак утвержд существование инерциальных систем - систем отсчёта, относительно которых свободная матер точка, не подверженная воздействию др тел, движется равномерно и прямолинейно(по инерции)) 2-й:
Ускорение, приобретаемое материальной
точкой (телом), пропорционально
вызывающей его силе, совпадает с ней
по направлению и обратно пропроц
массе материальной точки.
или
скорость
изменения импульса материальной
точки равна действующей на неё силе 3-й:
Всякое
действие матер точек (тел) друг на
друга имеет характер взаимодействия;
силы, с которыми действуют друг на
друга материальные точки, равны по
модулю, противоположны по направлению
и действуют вдоль одной прямой, соедин
эти точки:
третий закон позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что для системы матер точек взаимодействие сводится к силам парного взаимодействия между материальными точками. |
8. Энергия- универсальная мера различных форм движения и взаимодействия. Работа силы: количественная характеристика процесса обмена энергией между взаимодействующими телами. Элементарная
работа силы:
ds=/dr/- элементарный путь; Fs – проекция вектора F на вектор dr). Работа
силы на участке 1-2
и определяется площадью заштрихованной фигуры. Работа – скалярная величина.
Кинетическая энергия механической системы: энергия мех движения этой системы. Приращение кинетической энергии частицы на элементарном перемещении равно элементарной работе на том же перемещении: dE=dA. Это выражение можно расписать как:
Кинетическая энергия всегда положительна; неодинакова в разных инерциальных системах отсчёта; является функцией состояния системы. Мощность: физическая величина, характеризующая скорость совершения работы. ( N=dA/dt ) За время dt сила F совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени (N=Fdr/dt=Fv) т.е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка. Мощность – скалярная величина. Единицы работы: Дж (1 Дж – это работа, совершаемая силой 1Н на пути 1м: 1 Дж=1Н м) Единицы мощности: Вт (1 Вт – это мощность, при которой за время 1 с совершается работа 1 Дж: 1Вт=1Дж/с)
|
|
9. Консервативные силы: сила, работа которой при перемещении тела из одного положения в другое не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положения тела. (например гравитационные силы, кулоновские) Все другие силы (например силы трения) относятся к неконсервативным силам
Потенциальная энергия: мех энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная по координатам. Поэтому потенциальную энергию тела в каком-то определённом положении считают раной нулю (выбирают нулевой уровень), а энергию тела в др положениях отсчитывают относительно нулевого уровня. Потенциальная
энергия тела массой m
на высоте h
: Еп=mgh;
потенциальная энергия упругодеформированного
тела:
Потенциальная энергия системы, подобно кинетической, является функцией состояния системы. Она зависит от конфигурации системы и её положения по отношению к внешним силам. |
13.
Закон сохранения момента импульса:
момент импульса замкнутой системы
сохраняется, т.е. не изменяется с
течением времени:
Момент импульса твёрдого тела относительно оси есть сумма моментов импульса отдельных частиц:
Учитывая,
что
Это выражение – ещё одна форма уравнения динамики вращательного движения твёрдого тела относительно неподвижной оси: производная момента импульса твёрдого тел относительно оси равна моменту сил относительно той же оси. В
замкнутой системе момент внешних сил
М=0 и
|
|
|
10. Закон сохранения энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.е. не изменяется со временем. Ек+Еп=Е=const Это фундаментальный закон природы. Он является следствием однородности времени: инвариантности физических законов относительно выбора отсчёта времени. Диссипативные системы: система, в котрой механическая энергия постепенно уменьшается за счёт преобразования в другие (немеханические) формы энергии. Этот процесс получил название диссипации (рассеяния) энергии. Строго говоря, все системы в природе являются диссипативными. В системе, в которой действуют также неконсервативные силы, например силы трения, полная мех энергия системы не сохраняется. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии – сущность неуничтожимости материи и её движения. |
14. Момент инерции относительно неподвижной оси вращения: момент инерции системы (тела) относительно оси вращения есть физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
Т. Штейнера: Момент инерции тела относительно любой оси вращения равен моменту его инерции относ параллельной оси, проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния между осями. Момент
инерции тонкого стержня: (ось перпенд.
Стержню и проходит через его середину)
То
же ( но ось проходит через его конец)
Полый
тонкостенный цилиндр:
Кинетическая
энергия вращающегося тела: Абсолютно
тв тело вращается вокруг неподвижной
оси, разбивая его на элементарные
объёмами массами м1,м2,..,мn,
находящимися от оси на расстояниях
r1,r2,..,rn
запишем:
|
|
|
|
11. Абсолютно упругий удар: столкновение двух тел, в результате которого в обоих взаимодействующих телах не остаётся никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения энергии. Абсолютно неупругий удар: столкновение двух тел, в результате которого тела объединившись, двигаются дальше как единое целое. (например шары из пластелина) В данном случае закон сохранения энергии не соблюдается. Вследствии деформации происходит потеря кинетической энергии, перешедшей в другие формы энергии. Эту потерю можно определить по разности кинетической энергии тело до и после удара.
Если
ударяемое тело было первоначально
неподвижно, то
Если m2>>m1 ,то v<<v1 и почти вся кинетическая энергия при ударе переходит в другие виды энергии. |
15. Механический принцип относительности: законы динамики одинаковы во всех инерциальных системах отсчёта. Система К’ движется равномерно и прямолинейно со скоростью u (u-const) Скорость направлена вдоль ОО” , тогда вектор перемещения равен произведению скорости на время. В
основе механики лежат преобразования
Галилея. Преобразования
координат Галилея:
Задают связь между радиусами-векторами
или координатами произвольной точки
А
в обеих системах:
Основы классической физики в следующих 5-и постулатах:
Принцип эквивалентности: массу можно измерять из опытов по изучению движения объекта под действием какой-то силы. Исходя из m=F/a измеренная таким образом масса называется инертной. А
исходя из
Так
вот:
|
|
|
12.
Момент
силы относительно неподвижной точки
О:
Физическая величина, определяемая
векторным произведением радиус-вектора
r
, проведённого из точки О
в точку А
приложения силы, на силу F
:
Момент
силы относительно неподвижной оси
z:
Скалярная величина
Если
ось z
совпадает с направлением вектора М,
то момент силы представляется в виде
вектора, совпадающего с осью:
Момент
импульса относительно неподвижной
точки О:
Физическая величина, определяемая
произведением
Момент
импульса относительно неподвижной
оси z:
Скалярная
величина
|
16 Специальная теория относительности: специальная теория относительности основывается на двух постулатах Эйнштейна:
Преобразования
Лоренца (при
v=const.
Преобразования
Лоренца имеют следующий вид:
|

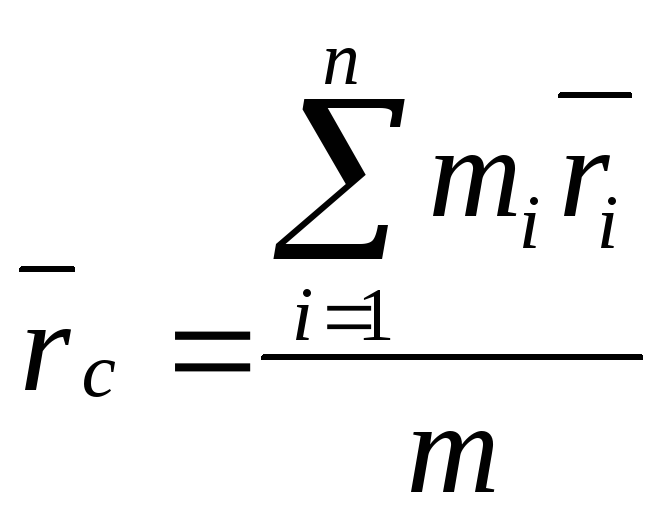 Где:
Где:
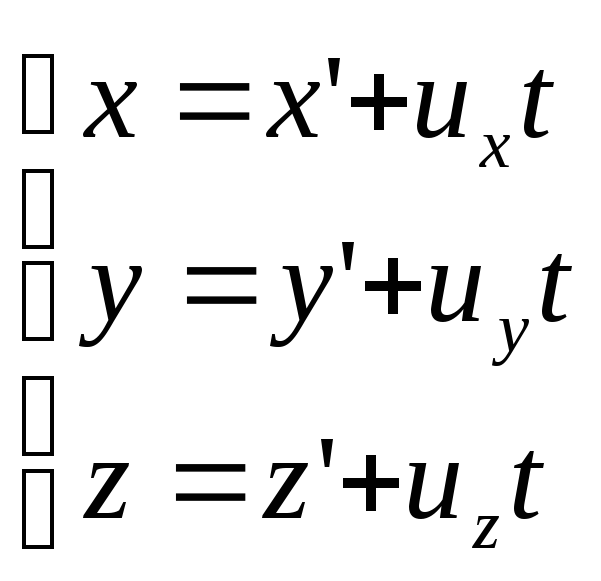 .Время
в системах протекает одинаково.
.Время
в системах протекает одинаково.