3. Теоретические сведения.

3.1. Оценка структур по вероятности достижения цели. Предположим, что в процессе исследования проблемы

1) исходная цель Z структуритована и разбита на m подцелей Z₁, Z₂, …, Z_m;

2) построено множество альтернативных структур, состоящее из n возможных вариантов S₁, S₂, …, S_n;

3) для оценки степени достижения каждой из частных целей Z₁, Z₂, …, Z_m сформировано множество из m критериев K₁, K₂, …, K_m;

4) построена матрица векторных оценок

	S1	S2	…	Sn
K1	k11	k12	…	k1n
K2	k21	k22	…	k2n
…	…	…	…	…
Km	km1	km2	…	kmn

Введем в рассмотрение: P_j – вероятность достижения конечной цели Z j-ой структурой S_j; p_ij – вероятность достижения промежуточной цели Z_i j-ой структурой S_j . Ставится задача: отсеять неперспективные структуры и сформировать множество перспективных структур, состоящее из таких структур S_j, для которых P_j≥p₀ (p₀ – пороговое значение).

Решение задачи основано на принципе Флейшмана: вероятность достижения цели Z не превышает вероятности достижения частной цели Z_i, т. е.

.

С этой целью:

1. Матрица векторных оценок приводится к безразмерному виду:

	S1	S2	…	Sn
K1	ρ11	ρ12	…	ρ1n
K2	ρ 21	ρ22	…	ρ2n
…	…	…	…	…
Km	ρm1	ρm2	…	ρmn

где

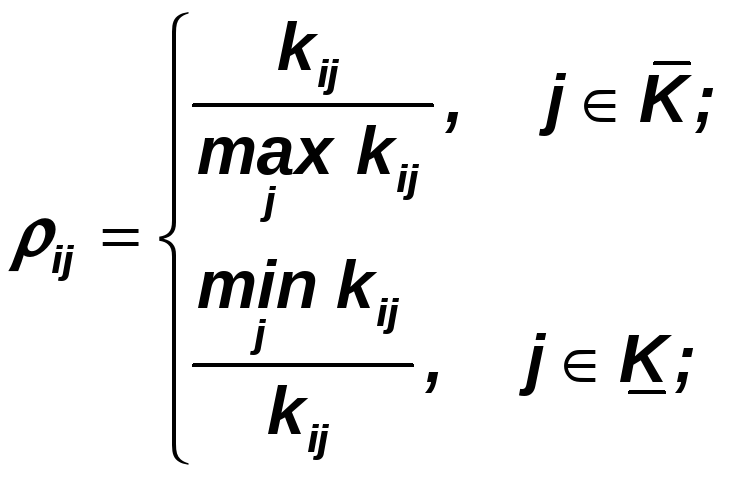
- множество индексов критериев, ориентированных на достижение максимума, - множество индексов критериев, ориентированных на достижение минимума.

2. Безразмерные оценки ρ_ij принимаются в качестве вероятностей достижения частных целей p_ij: p_ij=ρ_ij.

3. Находятся вероятности P_j достижения конечной цели Z j-ой структурой S_j:

.

Фактически P_j есть минимальное из чисел в j-ом столбце матрицы безразмерных оценок.

4. Отбираются варианты, для которых P_j≥p₀.

3.2. Ранжирование структур с использованием функций полезности. Одной из проблем при оценке структур с помощью многих критериев является существенная разница в диапазоне значений различных критериев. Практически любой алгоритм анализа структур прямо или косвенно содержит механизм приведения различных диапазонов значений к какому-то одному эталонному. Очень часто этот эталонный диапазон представляет собой отрезок [0, 1]. Рассмотрим один из способов приведения произвольного диапазона значений к отрезку [0, 1], основанный на использовании функций ценности.

Допустим, что критерий K имеет диапазон значений [k₁, k₂], при этом k₁ – (наи)худшее значение, k₂ – (наи)лучшее. Тогда функцию полезности ρ(k) можно построить следующим образом:

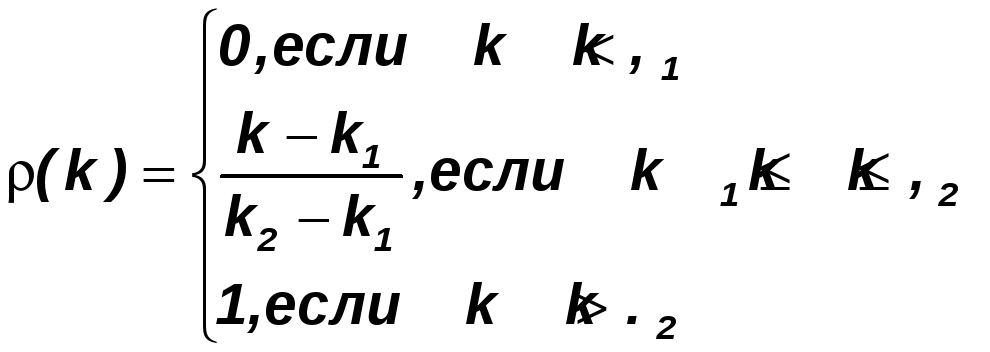(1)

Ниже приведен график этой функции

Рис.1. График функции полезности.

Худшему значению критерия соответствует нулевое значение функции полезности, лучшему – единичное значение.

Отметим, что диапазон значений [k₁, k₂] может не совпадать с множеством всех значений критерия K. Чаще всего реальный диапазон не известен, а интервал [k₁, k₂] получен от экспертов и описывает множество желательных значений критерия. Понимать это нужно таким образом: значения критерия на некоторых структурах могут лежать вне диапазона [k₁, k₂], т.е. быть лучше (больше) k₂ или хуже (меньше) k₁. Таким значениям критерия функция полезности (1) ставит в соответствие значения 1 и 0 соответственно. То, что значения, лучшие k₂, получают значение 1, вполне приемлемо. А вот, то что значения, худшие k₁ , получают, как и k₁, значение 0 – не всегда. Значения, худшие k₁, могут быть не только нежелательными, но и недопустимыми. Для того, чтобы подчеркнуть, что значения худшие худшего нежелательны, функции полезности «позволяют» принимать отрицательные значения. Формула (1) при этом принимает вид:

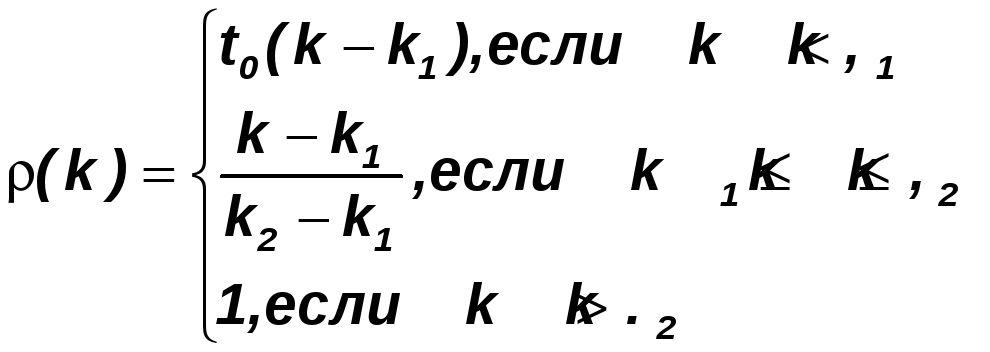(2)

График функции (2) приведен на рис. 2. Коэффициент t₀=tgφ «управляет» углом наклона φ и предназначен для учета степени нежелательности «плохих» значений критерия. Степень нежелательности высокая – коэффициент большой, степень нежелательности малая – коэффициент маленький.

Рис.1. График функции полезности (2).

Алгоритм метода анализа структур с использованием функций полезности может быть таким.

1. Формируем множество конкурирующих структур {S_j}.

2. Определяем совокупность частных критериев {K_i}.

3. Проводим опрос экспертов относительно худших и лучших значений критериев:

{Ki}	Единицы измерения	Худшее значение	Лучшее значение
K1	Еи1	k11	k12
K2	Еи2	k21	k22
…
Km	Еиm	km1	km2

4. Для частных критериев строим функции полезности (1), (2).

5. На основании опроса экспертов строим матрицу бинарных предпочтений критериев:

	K1	K2		Km	сj
K1		c12	…	c1m	c1
K2	c21		…	c2m	c2
…	…	…	…	…	…
Km	cm1	cm2	…		cm

где

6. Находим веса частных критериев, отражающие неформальные предпочтения экспертов:

.

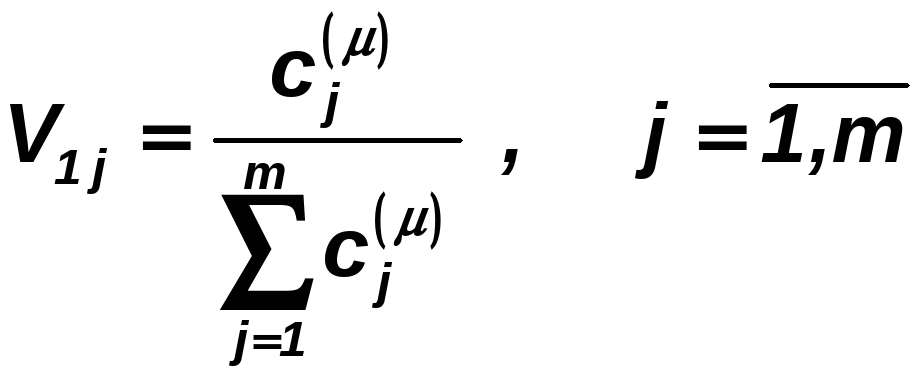7. Для оценки частных показателей разрабатываем соответствующие модели.

8. Строим матрицу векторных оценок

	S1	S2		Sn
K1	k11	k12	…	k1n
K2	k21	k22	…	k2n
…	…	…	…	…
Km	km1	km2	…	kmn

9. Находим веса частных показателей, исходя из разброса векторных оценок:

,

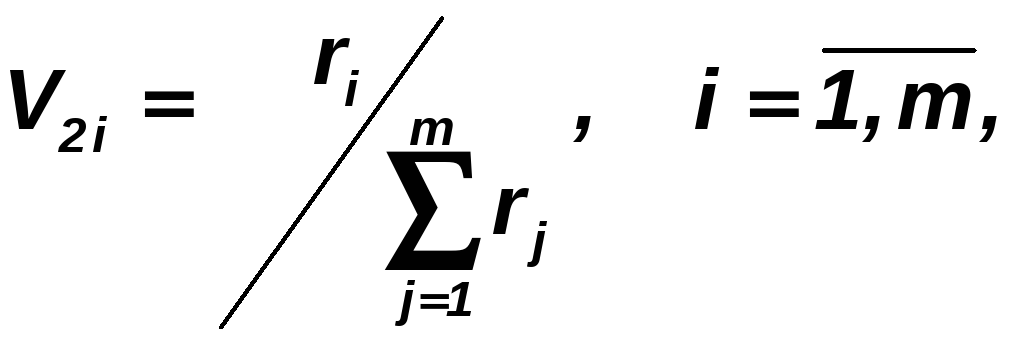где

.

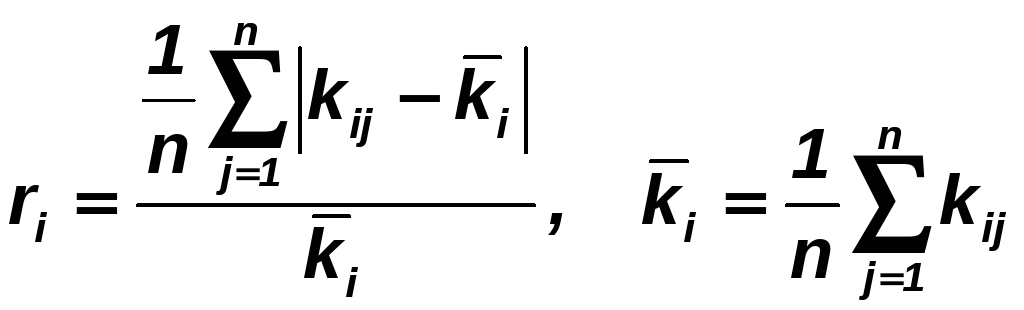10. Находим усредненные веса, характеризующие важность частных критериев:

11. Производим оценку полезности конкурирующих структур

	S1	S2		Sn	W
K1	ρ11	ρ12	…	ρ1n	W1
K2	ρ21	ρ22	…	ρ2n	W2
…	…	…	…	…	…
Km	ρm1	ρm2	…	ρmn	Wm
q	q1	q2	…	qn

Здесь

- оценки полезности, - функция полезности, соответствующая i-ому критерию;

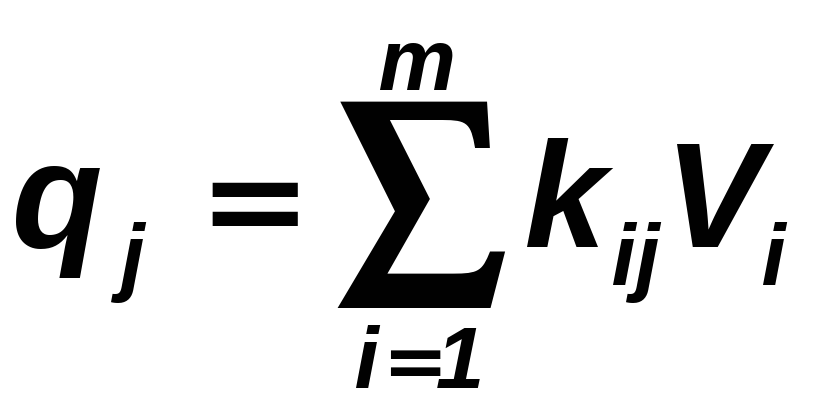- обобщенная оценка полезности структуры S_j, .

12. Ранжируем структуры в соответствии с обобщенными оценками полезности.