3.2.5. Расчет прочности нормальных сечений и подбор арматуры в расчетных сечениях балки

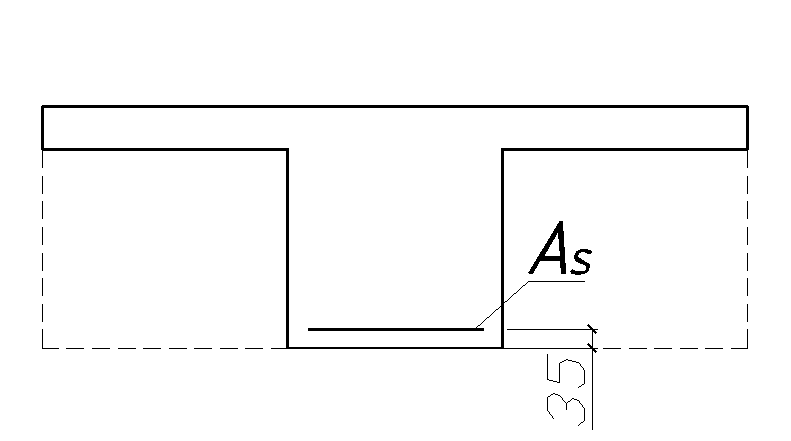
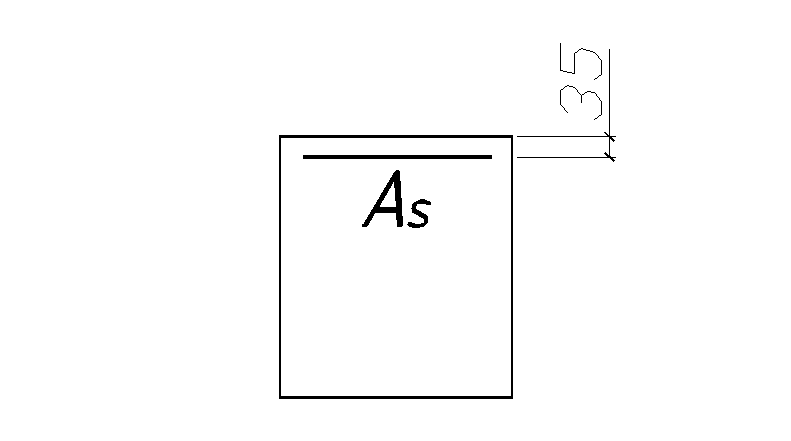
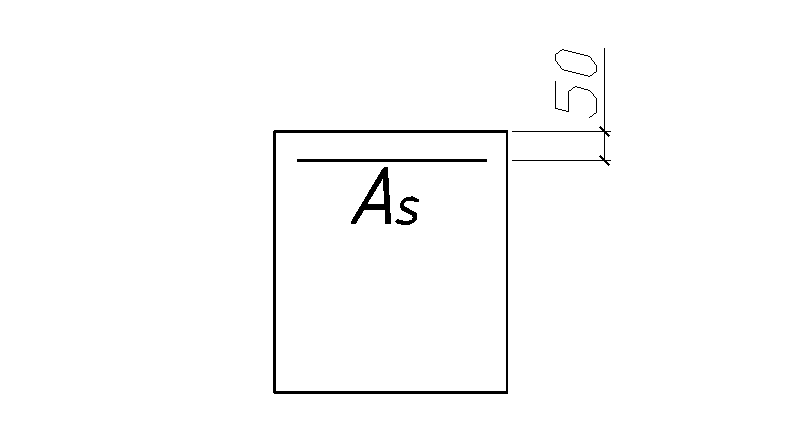
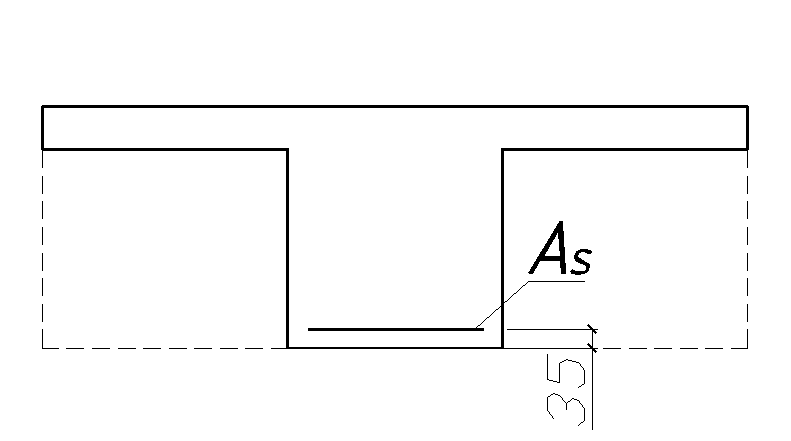
Определение требуемой площади сечения арматуры при действии положительного момента ведем как для таврового сечения с полкой в сжатой зоне. При действии отрицательного момента (полка) находится в растянутой зоне, следовательно расчетное сечение будет прямоугольным.

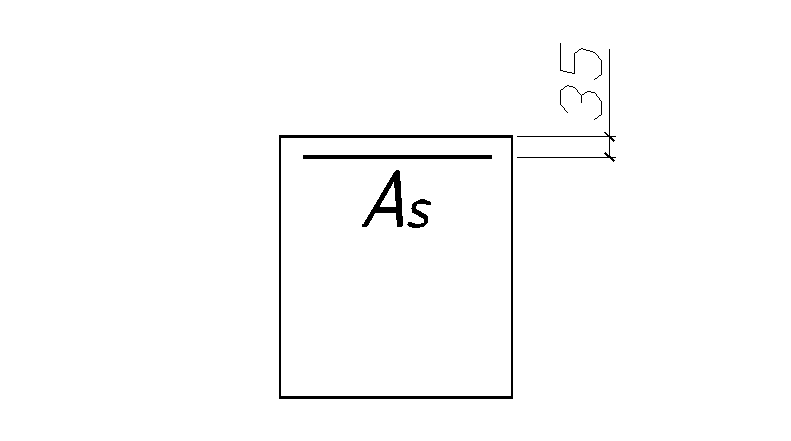
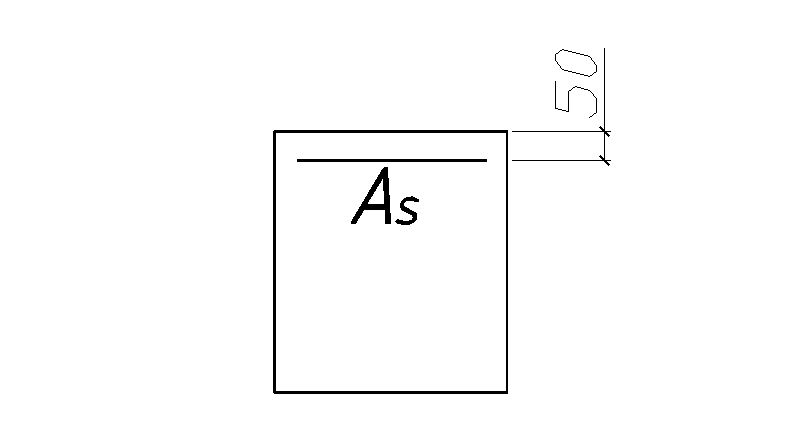
Размеры сечения принятые по расчету:

мм;мм;мм;мм.;

Принимаем величину мм в пролете, тогда:ммимм на опоре, тогда:мм.

Предположим, что нейтральная ось проходит по нижней грани полки, тогда область деформирования для прямоугольного сечения шириной будет следующая:

Данное значение лежит в пределах стадияIб.

По табл.3-3 прил.3[1] устанавливаем область деформирования. По табл.3-3 прил.3[1] определяем :

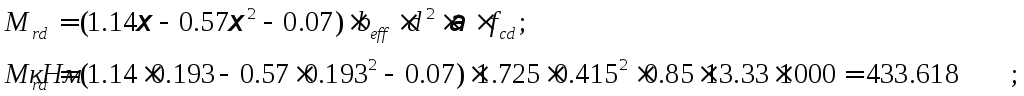Т.к условие()выполняется, то нейтральная ось проходит в пределах полки, сечение рассчитывается как прямоугольное с шириной.

Расчет продольной арматуры второстепенной балки ведут в следующей последовательности:

Для бетона класса Спринимаем

Для арматуры S400: .

Определяем

В пролете 1(нижняя арматура): ; м;м.

;растянутая арматура достигла предельных деформаций.

;

В пролете 2(нижняя арматура): ; м; м.

;

;

.

В опорных сечениях действуют отрицательные моменты, плита расположена в растянутой зоне, поэтому сечения балки рассматриваются как прямоугольные шириной м.

На опоре В(верхняя арматура): ; м; м.

;

;

.

В пролете 2(верхняя арматура): ; м; м.

;

;

На опоре С (верхняя арматура):

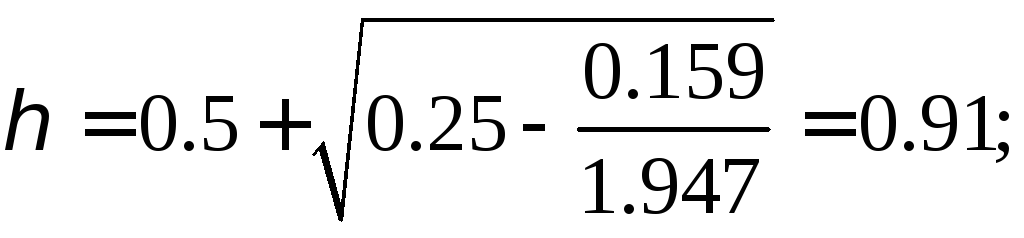
Результаты расчетов сводим в таблицу 7.

Таблица7 Определение площади сечения рабочей арматуры второстепенной балки

Положение сечения	Расположение арматуры	М, кНм	Расчетное сечение			, см2		, см2	Приня-тое армирование
1 пролет	Нижняя	87.14		0.026	0.986	5.83		6.28
1 пролет	Верхняя	–		Монтажная конструктивная арматура				2.26
Опора В	Верхняя	-68.47		0.19	0.89		5.27	6.28
2 пролет	Нижняя	57.79		0.017	0.99		3.85	4.211
2 пролет	Верхняя	-13.87		0.036	0.981		1.245	2.26
Опора C	Верхняя	-57.79		0.159	0.91		4.35	5.151

3.2.6. Расчет прочности наклонных сечений по поперечной силе.

Расчет прочности железобетонных элементов на действие поперечных сил производиться из условия:

где: - расчетная поперечная сила от внешних воздействий;

- поперечная сила, воспринимаемая ж/б элементом без поперечного армирования.

Сначала определяем поперечную силу, которую может воспринять второстепенная балка без поперечного армирования (хомутов). Расчет выполняем для сечения у первой промежуточной опоры (опоры В) слева, где действует наибольшая поперечная сила.

Рис. 10. Расположение расчётных сечений для второстепенной балки.

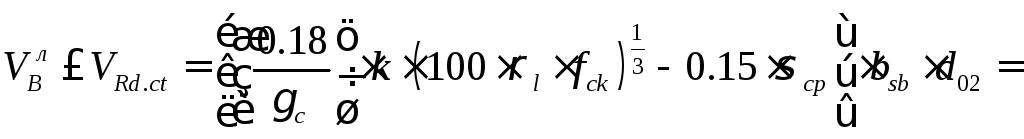
, но не менее

где:

;;;

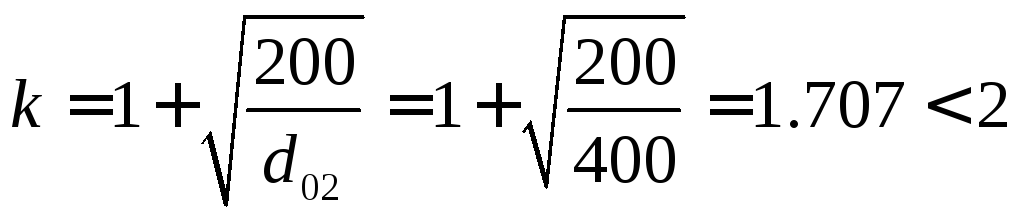
- усилие от предварительного напряжения.

Поскольку ,то необходима постановка поперечной арматуры по расчету. Расстояние от опоры, на котором требуется установка хомутов по расчету:

Первое расчетное сечение назначаем на расстоянии от опоры:

, что составляет

В данном сечении усилия составляют:

Определяем продольные относительные деформации в растянутой арматуре, предварительно задавшись углом наклона диагональных трещин к горизонтали и расстоянием между верхней и нижней арматурами

Для выяснения правильности выбора угла определяем касательные напряжения, действующие в рассматриваемом сечении:

Отношение

где принимается по таблице 6.1[2]

В соответствии со значением ипо табл. 3-1 [3] уточняем угол наклона диагональной трещины ()

Среднее значение главных растягивающих деформаций

Главные растягивающие напряжения:

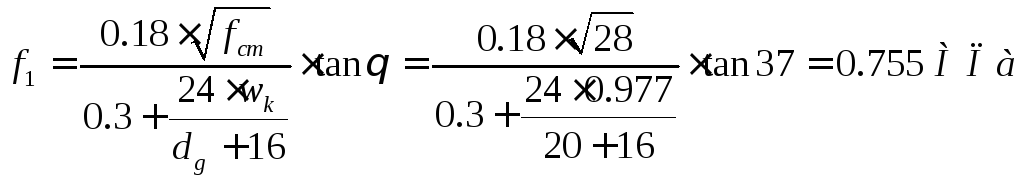
где: – максимальный размер заполнителя (=20мм)

- ширина раскрытия наклонной трещины

=300мм– расстояние между диагональными трещинами

Составляющая поперечной силы, воспринимаемая бетоном:

Составляющая поперечной силы, которую должна воспринять арматура (хомуты)

Составляющая поперечной силы, воспринимаемая поперечной арматурой определяется по формуле:

, откуда

.

где - угол наклона поперечной арматуры (хомутов) к продольной оси балки.

расчетное сопротивление поперечной арматуры.

(для арматуры классаS240).

Приняв, в соответствии с п.11.2.21[2] шаг хомутов , что не превышаети, вычисляем площадь поперечного сечения хомутов:

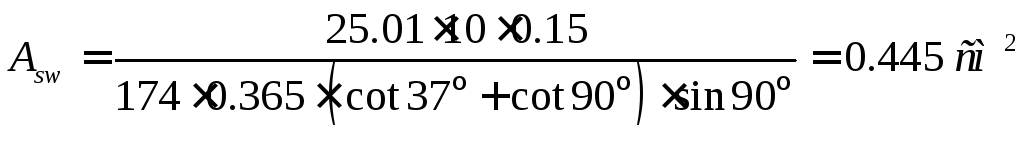
Принимаемая площадь поперечного сечения хомутов должна быть не менее:

где: коэффициент поперечного армирования сечения, принимается по табл.11.2 [2]

Окончательно принимаем двухсрезные хомуты диаметром 6 мм(A_sw=0.57см²) классаS240 и устанавливаем в опорной зоне длиной 0.25 cшагом 150мм.

Составляющая поперечной силы, которую может воспринять арматура равна:

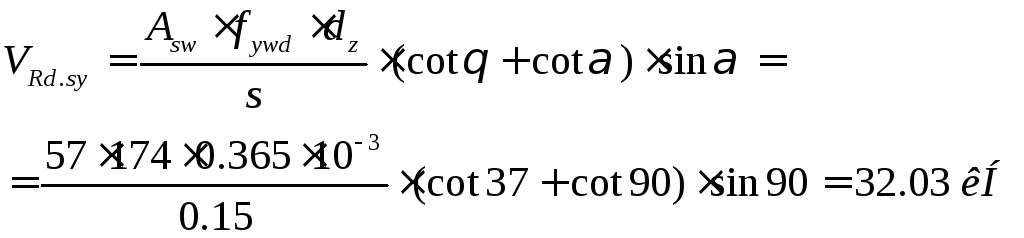
Действительная несущая способность наклонного сечения составит:

Проверяем условие:

В средних частях пролётов шаг поперечных стержней должен назначаться независимо от высоты сечения не более 3/4h не более 50см. ПринимаемS=30см, что не превышает 3/4h=3/445=33.75см.

В остальных сечениях расчеты производятся аналогично. В данной работе у крайней опоры () и у первой промежуточной опоры справа () , где поперечные силы меньше, чем на опореBслева () , принятое поперечное армирование так же будет обеспечивать прочность наклонных сечений. Уменьшить поперечное армирование не представляется возможным, так как диаметр хомутов принят минимальным, а шаг – максимально допустимым по конструктивным требованиям при данной высоте балки.