V. Функции нескольких переменных (фнп).
Что называется ФНП? Что называется областью определения и областью значений ФНП? Что называется границей области определения? Какая область называется открытой, замкнутой?
Что называется пределом ФНП? Какой геометрический смысл предела функции двух переменных в точке?
Какая ФНП называется непрерывной в точке
?
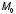Какая ФНП называется непрерывной в
области?Что называют частной производной ФНП в точке? Какая ФНП называется дифференцируемой в точке
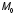?Что называют полным приращением ФНП в точке
.
Что называют дифференциалом ФНП в точке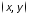
?Как используется дифференциал в приближенных вычислениях? Запишите формулу.
Что называется производной функции
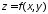в точке
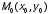по направлению вектора
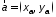?Что называется градиентом функции
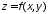в точке
.
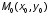Как называется направление, противоположное
направлению вектора градиента? Докажите,
что вектор градиент указывает направление
наискорейшего возрастания функции.Что называется касательной плоскостью к поверхности. Запишите уравнение касательной плоскости, если функция задана: явно
;
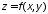неявно уравнением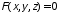
.Что называется нормалью к поверхности. Запишите уравнение нормали, если функция задана: явно
;
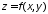неявно уравнением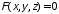
.Что называют точкой максимума, минимума, экстремума ФНП? Что называют экстремумами ФНП? Сформулируйте необходимое условие экстремума ФНП.
Какие точки называют стационарными точками функции
?
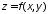Что называют матрицей Гессе? Сформулируйте
достаточное условие экстремума ФНП.
Доказать.
Получите формулу производной функции
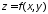в точке
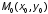по направлению вектора
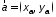?Пусть функции
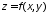дифференцируема в точке
.
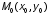Получите формулу касательной плоскости
и нормали к поверхности, определяемой
этой функцией.Используя метод наименьших квадратов, получить формулы для нахождения неизвестных параметров a и b линейной функции
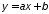.Используя метод наименьших квадратов, получить формулы для нахождения неизвестных параметров a, b и c квадратичной функции
.
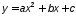