Решение

Система может быть записана в виде

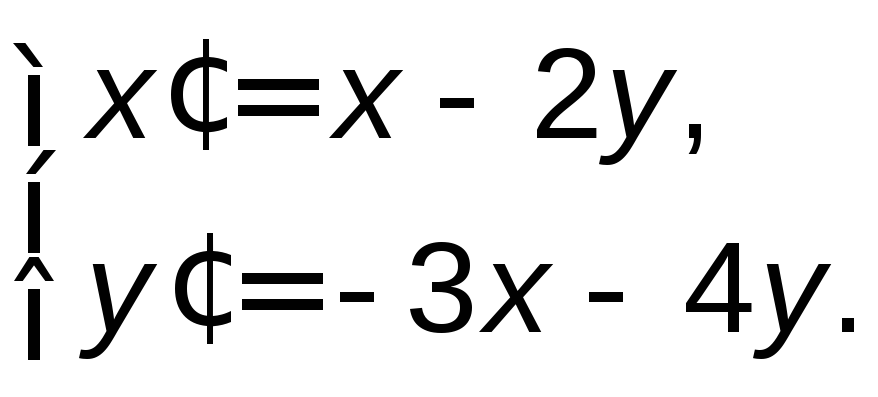
Продифференцируем первое уравнение системы. Получим

.

Заменим в полученном уравнении выражением из второго уравнения системы

.

Выразим из первого уравнения и подставим в полученное уравнение

,

.

Откуда

.

Получили линейное однородное дифференциальное уравнение второго порядка с коэффициентами. Общее решение которого имеет вид:

.

Найдем производную :

.

Подставляя значения ив выражения для, найдем

,

.

Таким образом, решение системы имеет вид

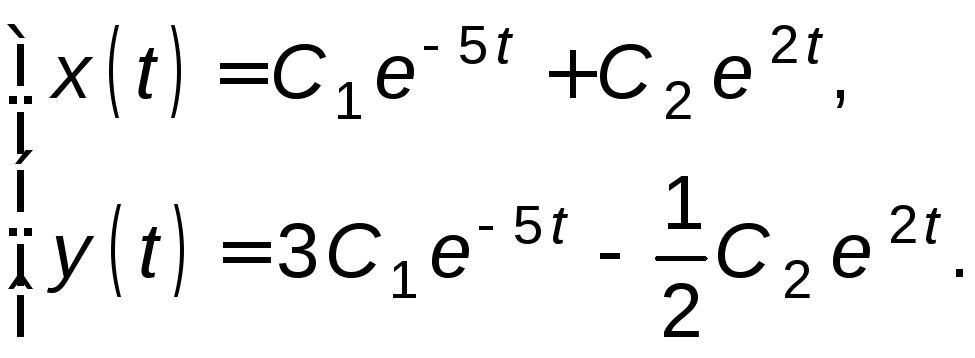
Ответ.

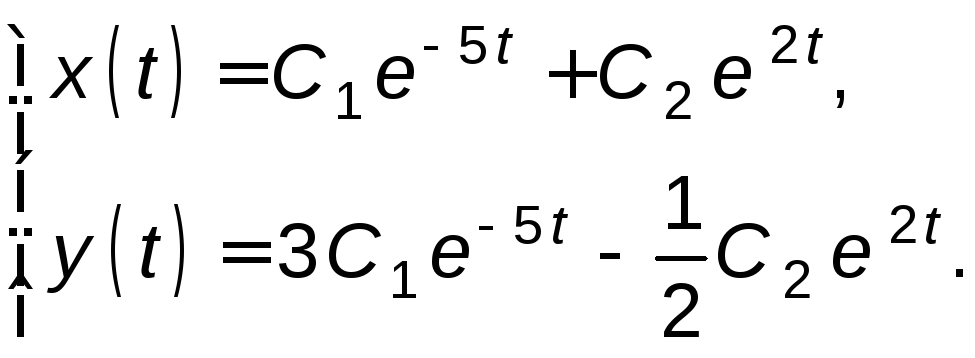
Задание 6. Вычислить массу материальной пластины, занимающей область плоскости, если поверхностная плотностьи границы областизаданы уравнениями,.

Решение

Масса материальной пластины с поверхностной плотностью , занимающей область, определяется по формуле:

.

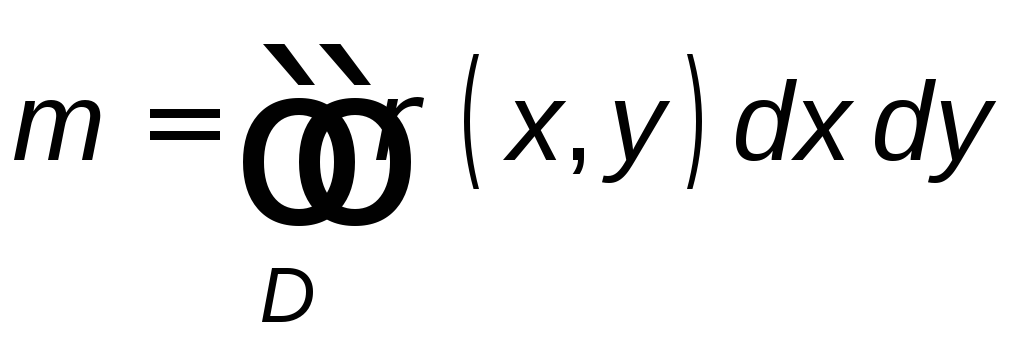Построим область .

Координаты точек пересечения линий найдем из системы:

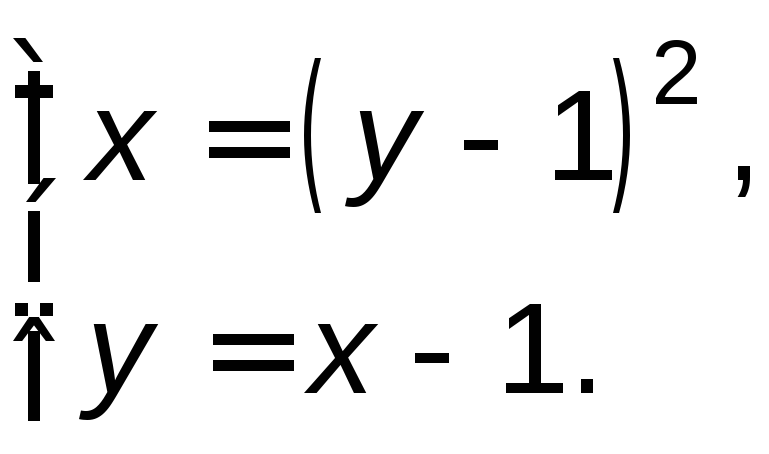
Решением системы являются значения:и. Значит, линии пресекаются в точкахи.

Область – правильная относительно оси.

Тогда

.

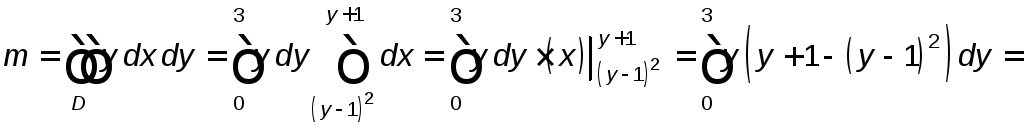
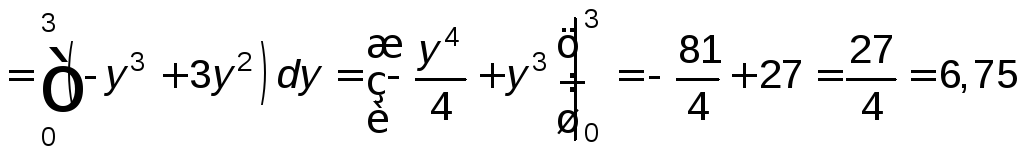Ответ. 6,75.

Задание 7. Используя кратные интегралы, вычислить объём тела, ограниченного указанными поверхностями: ,,,,. Сделать чертёж.

Решение

Определим типы поверхностей, ограничивающих тело:

–параболоид вращения;

–плоскость, параллельная оси ;

x=0 – плоскость ;

y=0 – плоскость ;

z=0 – плоскость .

Изобразим данное тело

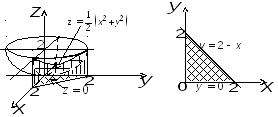
Вычислим объём с помощью тройного интеграла. Так как тело расположено правильно относительно оси , то объем этого тела найдем по формуле:

.

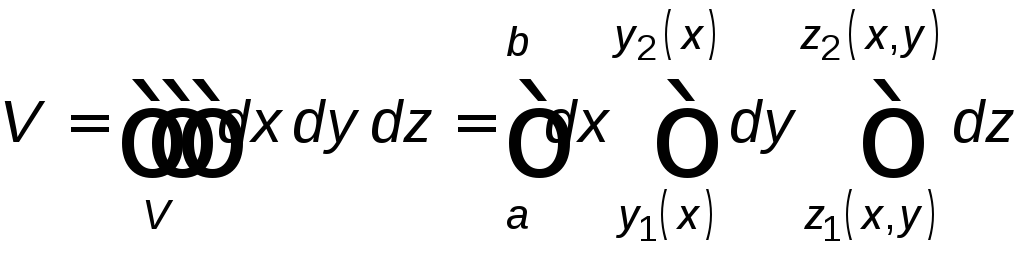Подставляя данные в формулу, получим:

.

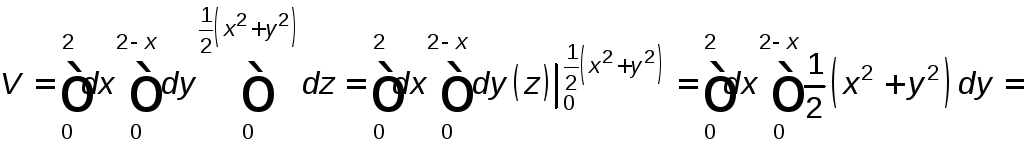
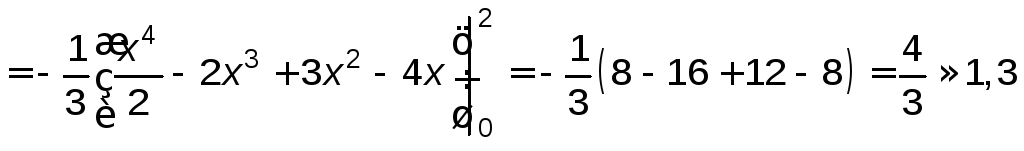Ответ. 1,3.

Задание 8. Вычислить криволинейный интеграл

,

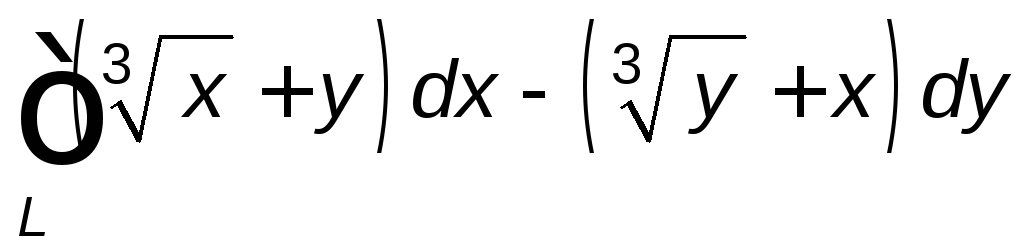где верхняя дуга астроиды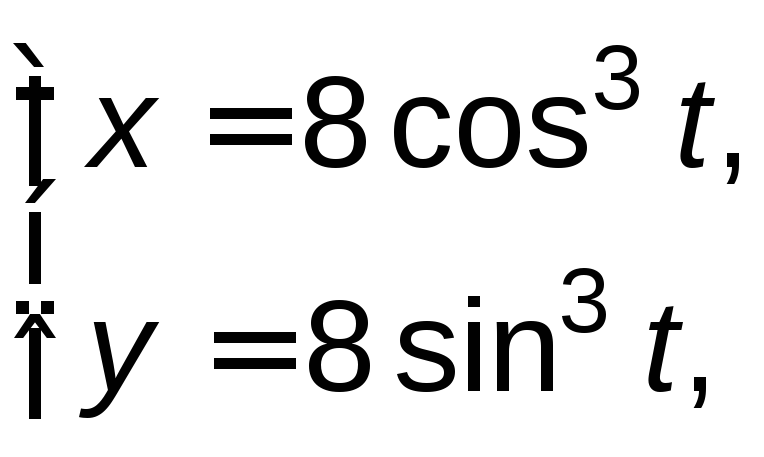от точкидо точки. Сделать чертёж.

Решение

Сделаем чертёж

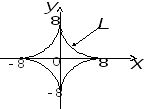
При перемещении вдоль кривой от точкидо точки, параметрбудет изменяться отдо: подставили, координаты начальной и конечной точек дуги в уравнение астроиды.

Найдем и:

,

.

Подставим найденные выражения в подынтегральное выражение

.

Тогда

.

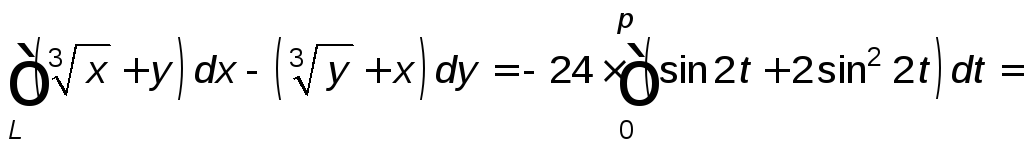
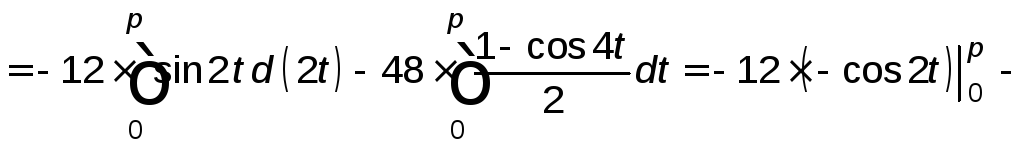
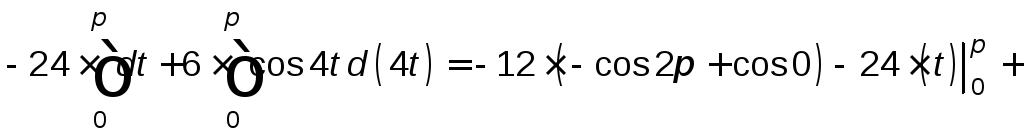
Ответ. .

Литература

1. Пискунов Н. С. Дифференциальное и интегральное исчисление Т. 2. - M.: Наука, 1985.

2. Жевняк Р. М., Карпук А. А. Высшая математика, ч.2,3. – Минск: ВШ, 1984-1988.

3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. - M.: Наука, 1985.

4. Сборник задач по математике для втузов (под ред. А. В. Ефимова и Б. П. Демидовича, ч.2). - M.: Наука, 1981 г.

5. Сборник индивидуальных заданий по высшей математике (под ред. А.П. Рябушко, ч. 2-3.). – Минск: ВШ, 2000.

6. Гусак А.А. Высшая математика, т.2. – Минск: ВШ, 1988.

7. Гусак А.А. Пособие к решению задач по высшей математике. – Минск: ВШ, 1988.

8. Тузик А.И. Интегрирование функций одной и нескольких переменных. – Брест: Изд-во БГТУ, 2000.

Содержание

Организационно-методические указания………………………………..	3
Контрольные вопросы курса “Высшая математика” ………………..…	3
Контрольная работа №2………………………….…………………………	6
Задание 1…………………………………………………………………..	6
Задание 2…………………………………………………………………..	9
Задание 3…………………………………………………………………..	10
Задание 4…………………………………………………………………..	11
Задание 5…………………………………………………………………..	12
Задание 6…………………………………………………………………..	13
Задание 7…………………………………………………………………..	14
Задание 8…………………………………………………………………..	15
Рекомендации к выполнению контрольной работы №2..……………..	19
Задание 1…………………………………………………………………..	19
Задание 2…………………………………………………………………..	22
Задание 3…………………………………………………………………..	23
Задание 4…………………………………………………………………..	25
Задание 5…………………………………………………………………..	29
Задание 6…………………………………………………………………..	30
Задание 7…………………………………………………………………..	31
Задание 8…………………………………………………………………..	32
Литература……………………………………………………………………	34