
- •Министерство образования Республики Беларусь
- •«Брестский государственный технический университет» Кафедра высшей математики
- •Организационно-методические указания
- •Контрольные вопросы курса «Высшая математика»
- •II семестр
- •Рекомендации к выполнению контрольной работы №2
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Учебное издание
- •224017, Г. Брест, ул. Московская, 267.
II семестр
Комплексные числа.
Различные формы записи комплексных чисел. Геометрическое изображение комплексного числа.
Действия над комплексными числами. Понятие комплексной функции действительного аргумента.
Первообразная функции.
Неопределенный интеграл и его свойства.
Табличное интегрирование.
Интегрирование подстановкой.
Интегрирование по частям.
Интегрирование простейших дробей.
Интегрирование иррациональных выражений.
Интегрирование рациональных дробей.
Интегрирование тригонометрических выражений.
Интегралы, не выражающиеся через элементарные функции.
Задача о площади криволинейной трапеции.
Определенный интеграл, его геометрический и механический смыслы.
Основные свойства определенного интеграла.
Интегралы с переменным верхним пределом. Формула Ньютона-Лейбница.
Замена переменных в определенном интеграле.
Интегрирование по частям в определенном интеграле.
Несобственные интегралы первого рода. Признаки сходимости.
Несобственные интегралы второго рода. Признаки сходимости.
Площадь плоской фигуры в декартовой системе координат.
Площадь плоской фигуры в полярных координатах.
Вычисление объема тела по параллельным сечениям. Вычисление объемов тел вращения.
Дифференциал длины дуги. Вычисление длины дуги кривой.
Кривизна плоской кривой. Радиус и круг кривизны. Эволюта и эвольвента кривой.
Работа переменной силы.
Масса неоднородного стержня.
Статические моменты и координаты центра тяжести гладкой кривой. Моменты инерции плоской кривой.
Центр масс плоской пластинки.
Понятие дифференциального уравнения. Физические задачи, приводящие к дифференциальным уравнениям первого порядка. Задача Коши.
Теорема существования и единственности решения задачи Коши. Понятие общего решения. Особое решение.
Дифференциальные уравнения с разделяющимися переменными.
Однородные дифференциальные уравнения и уравнения, приводящие к ним.
Линейные дифференциальные уравнения.
Уравнение Бернулли.
Понятие дифференциального уравнения высшего порядка. Задача Коши.
Дифференциальные уравнения, допускающие понижение порядка. Задачи о второй космической скорости и изгибе стержня.
Однородные линейные дифференциальные уравнения.
Линейный дифференциальный оператор, его свойства.
Свойства решений однородных дифференциальных уравнений.
Линейная независимость функций. Определитель Вронского. Теорема о структуре общего решения однородного дифференциального уравнения.
Структура общего решения неоднородного дифференциального уравнения. Принцип суперпозиции решений.
Метод Лагранжа (метод вариации произвольных постоянных).
Понижение порядка неоднородных дифференциальных уравнений.
Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Метод Эйлера.
Однородные линейные дифференциальные уравнения высших порядков с постоянными коэффициентами.
Линейные дифференциальные уравнения второго порядка со специальной правой частью.
Системы дифференциальных уравнений: общие понятия, фазовая плоскость, фазовые траектории. Метод исключения.
Линейные однородные системы дифференциальных уравнений с постоянными коэффициентами.
Задачи, приводящие к понятию двойного интеграла.
Определение, свойства и вычисление двойного интеграла.
Двойной интеграл в полярных координатах.
Вычисление объемов.
Масса тонкой пластинки.
Статические моменты и координаты центра тяжести пластинки. Момент инерции пластинки.
Задачи, приводящие к понятию тройного интеграла.
Определение и свойства тройного интеграла.
Вычисление тройного интеграла.
Тройной интеграл в цилиндрических и сферических координатах.
Объем и масса тела.
Статические моменты и координаты центра тяжести тела. Моменты инерции тела.
Задача, приводящая к понятию криволинейного интеграла по дуге.
Определение и свойства криволинейного интеграла первого рода.
Вычисление криволинейного интеграла первого рода.
Приложения криволинейного интеграла первого рода.
Работа переменной силы. Линейный интеграл.
Определение, свойства и вычисление линейного интеграла.
Связь линейного интеграла с криволинейным интегралом первого рода.
Независимость линейного интеграла от пути интегрирования.
Приложения линейного интеграла. Формула Грина.
Контрольная работа №2
Задание 1. Найти неопределенные интегралы (результаты в случаях а), б) и в) проверить дифференцированием).
|
1.1. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.2. |
а) |
б) |
в) |
|
|
г)
|
д)
|
|
|
1.3. |
а) |
б) |
в) |
|
|
г) |
д) |
|
|
1.4. |
а) |
б) |
в) |
|
|
г) |
д) |
|
|
1.5. |
а) |
б) |
в) |
|
|
г) |
д) |
|
|
1.6. |
а) |
б) |
в) |
|
|
г) |
д) |
|
|
1.7. |
а) |
б) |
в) |
|
|
г) |
д) |
|
|
1.8. |
а) |
б) |
в) |
|
|
г) |
д) |
|
|
1.9. |
а) |
б) |
в) |
|
|
г) |
д) |
|
|
1.10. |
а) |
б) |
в) |
|
|
г) |
д) |
|
|
1.11. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.12. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.13. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.14. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.15. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.16. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.17. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.18. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.19. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.20. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.21. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.22. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.23. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.24. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.25. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.26. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.27. |
а)
|
б)
|
в)
|
|
|
г)
|
д)
|
|
|
1.28. |
а) |
б) |
в) |
|
|
г) |
д) |
|
|
1.29. |
а) |
б) |
в) |
|
|
г) |
д) |
|
|
1.30. |
а) |
б) |
в) |
|
|
г) |
д) |
|
Задание 2. Вычислить определенный интеграл.
|
2.1. |
|
2.11. |
|
2.21. |
|
|
2.2. |
|
2.12. |
|
2.22. |
|
|
2.3. |
|
2.13. |
|
2.23. |
|
|
2.4. |
|
2.14. |
|
2.24. |
|
|
2.5. |
|
2.15. |
|
2.25. |
|
|
2.6. |
|
2.16. |
|
2.26. |
|
|
2.7. |
|
2.17. |
|
2.27. |
|
|
2.8. |
|
2.18. |
|
2.28. |
|
|
2.9. |
|
2.19. |
|
2.29. |
|
|
2.10. |
|
2.20. |
|
2.30. |
|
Задание 3. Найти общее решение дифференциального уравнения
|
3.01. |
|
3.02. |
|
|
3.03. |
|
3.04. |
|
|
3.05. |
|
3.06. |
|
|
3.07. |
|
3.08. |
|
|
3.09. |
|
3.10. |
|
|
3.11. |
|
3.12. |
|
|
3.13. |
|
3.14. |
|
|
3.15. |
|
3.16. |
|
|
3.17. |
|
3.18. |
|
|
3.19. |
|
3.20. |
|
|
3.21. |
|
3.22. |
|
|
3.23. |
|
3.24. |
|
|
3.25. |
|
3.26. |
|
|
3.27. |
|
3.28. |
|
|
3.29. |
|
3.30. |
|
Задание 4. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям.
|
4.1. |
|
|
|
|
4.2. |
|
|
|
|
4.3. |
|
|
|
|
4.4. |
|
|
|
|
4.5. |
|
|
|
|
4.6. |
|
|
|
|
4.7. |
|
|
|
|
4.8. |
|
|
|
|
4.9. |
|
|
|
|
4.10. |
|
|
|
|
4.11. |
|
|
|
|
4.12. |
|
|
|
|
4.13. |
|
|
|
|
4.14. |
|
|
|
|
4.15. |
|
|
|
|
4.16. |
|
|
|
|
4.17. |
|
|
|
|
4.18. |
|
|
|
|
4.19. |
|
|
|
|
4.20. |
|
|
|
|
4.21. |
|
|
|
|
4.22. |
|
|
|
|
4.23. |
|
|
|
|
4.24. |
|
|
|
|
4.25. |
|
|
|
|
4.26. |
|
|
|
|
4.27. |
|
|
|
|
4.28. |
|
|
|
|
4.29. |
|
|
|
|
4.30. |
|
|
|
Задание 5. Найти общее решение системы дифференциальных уравнений методом исключения.
|
5.1. |
|
5.11. |
|
5.21. |
|
|
5.2. |
|
5.12. |
|
5.22. |
|
|
5.3. |
|
5.13. |
|
5.23. |
|
|
5.4. |
|
5.14. |
|
5.24. |
|
|
5.5. |
|
5.15. |
|
5.25. |
|
|
5.6. |
|
5.16. |
|
5.26. |
|
|
5.7. |
|
5.17. |
|
5.27. |
|
|
5.8. |
|
5.18. |
|
5.28. |
|
|
5.9. |
|
5.19. |
|
5.29. |
|
|
5.10. |
|
5.20. |
|
5.30. |
|
Задание
6.
Вычислить массу материальной пластины,
занимающей область
![]() плоскости
плоскости![]() ,
если поверхностная плотность
,
если поверхностная плотность![]() и границы области
и границы области![]() заданы уравнениями:
заданы уравнениями:
|
6.1. |
|
|
|
6.2. |
|
|
|
6.3. |
|
|
|
6.4. |
|
|
|
6.5. |
|
|
|
6.6. |
|
|
|
6.7. |
|
|
|
6.8. |
|
|
|
6.9. |
|
|
|
6.10. |
|
|
|
6.11. |
|
|
|
6.12. |
|
|
|
6.13. |
|
|
|
6.14. |
|
|
|
6.15. |
|
|
|
6.16. |
|
|
|
6.17. |
|
|
|
6.18. |
|
|
|
6.19. |
|
|
|
6.20. |
|
|
|
6.21. |
|
|
|
6.22. |
|
|
|
6.23. |
|
|
|
6.24. |
|
|
|
6.25. |
|
|
|
6.26. |
|
|
|
6.27. |
|
|
|
6.28. |
|
|
|
6.29. |
|
|
|
6.30. |
|
|
Задание 7. Используя кратные интегралы, вычислить объём тела, ограниченного указанными поверхностями. Сделать чертёж.
|
7.1. |
|
|
7.2. |
|
|
7.3. |
|
|
7.4. |
|
|
7.5. |
|
|
7.6. |
|
|
7.7. |
|
|
7.8. |
|
|
7.9. |
|
|
7.10. |
|
|
7.11. |
|
|
7.12. |
|
|
7.13. |
|
|
7.14. |
|
|
7.15. |
|
|
7.16. |
|
|
7.17. |
|
|
7.18. |
|
|
7.19. |
|
|
7.20. |
|
|
7.21. |
|
|
7.22. |
|
|
7.23. |
|
|
7.24. |
|
|
7.25. |
|
|
7.26. |
|
|
7.27. |
|
|
7.28. |
|
|
7.29. |
|
|
7.30. |
|
Задание
8.
Вычислить данный криволинейный интеграл
вдоль линии ![]() .
Сделать чертёж.
.
Сделать чертёж.
|
8.1. |
где
|
|
8.2. |
где
|
|
8.3. |
где
|
|
8.4. |
где
|
|
8.5. |
где
|
|
8.6. |
где
|
|
8.7. |
где
|
|
8.8. |
где
|
|
8.9. |
где
|
|
8.10. |
где
|
|
8.11. |
где
|
|
8.12. |
где
|
|
8.13. |
где
|
|
8.14. |
где
|
|
8.15. |
где
|
|
8.16. |
где
|
|
8.17. |
где
|
|
8.18. |
где
|
|
8.19. |
где
|
|
8.20. |
где
|
|
8.21. |
где
|
|
8.22. |
где
|
|
8.23. |
где
|
|
8.24. |
где
|
|
8.25. |
где
|
|
8.26. |
где
|
|
8.27. |
где
|
|
8.28. |
где
|
|
8.29. |
где
|
|
8.30. |
|

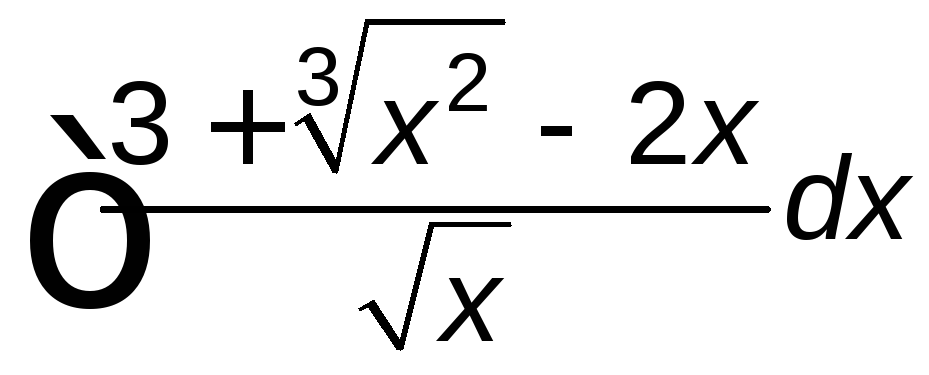 ;
;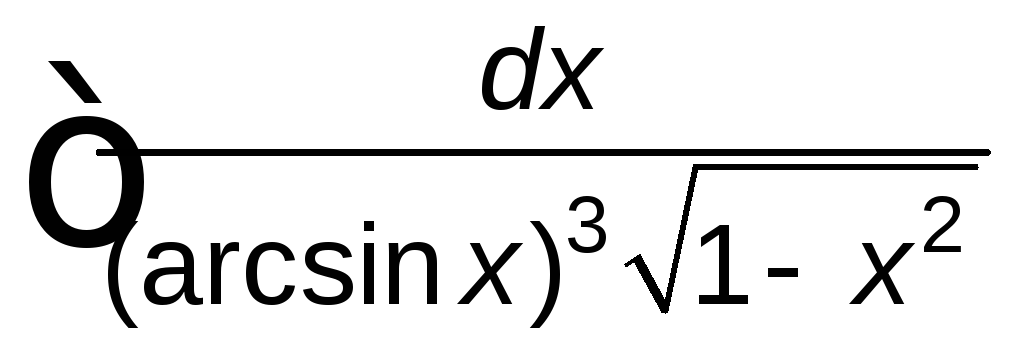 ;
;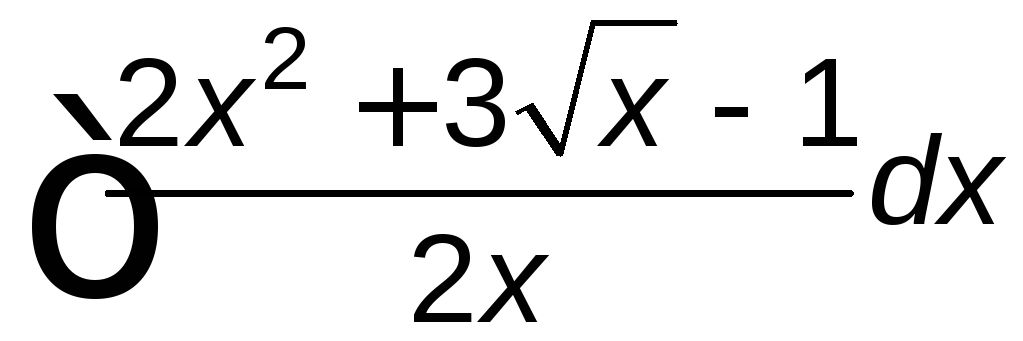 ;
;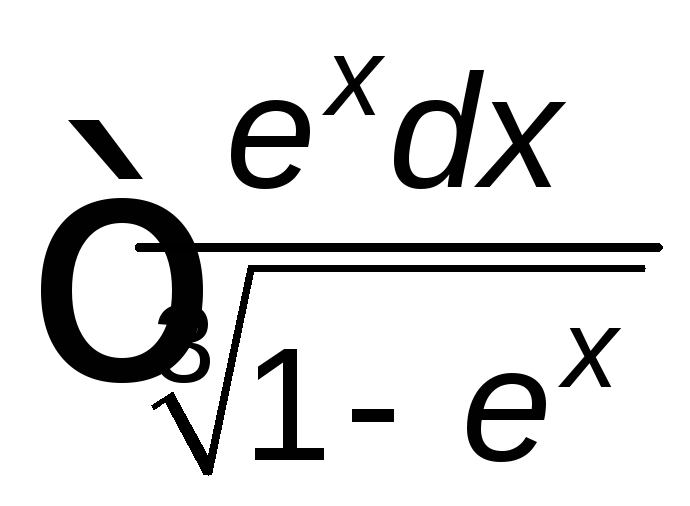 ;
;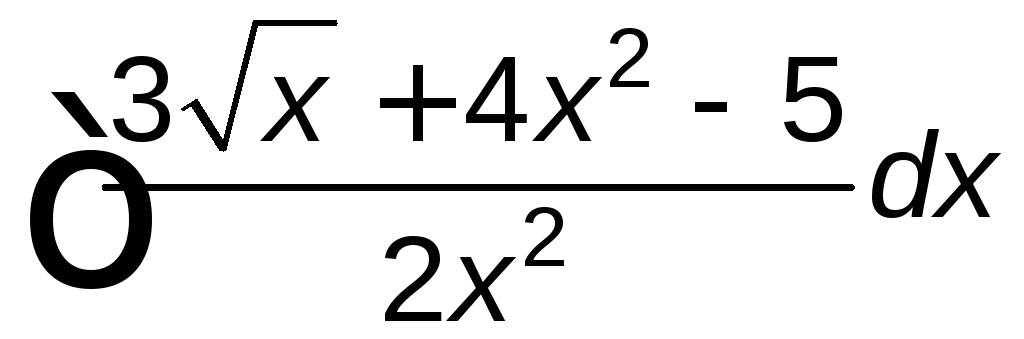 ;
;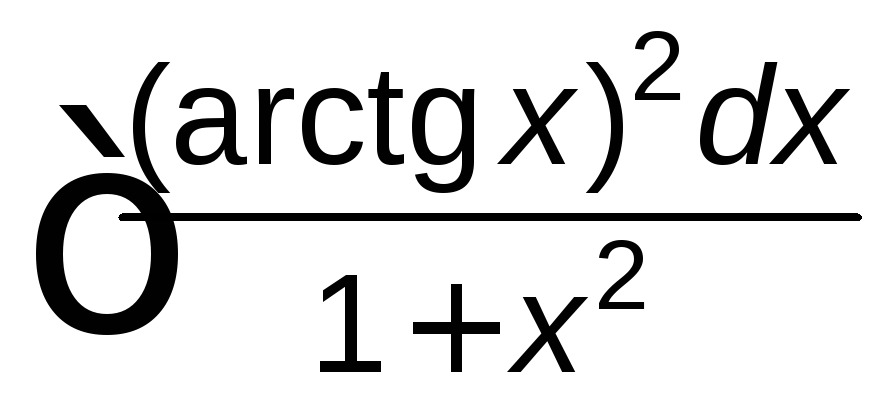 ;
;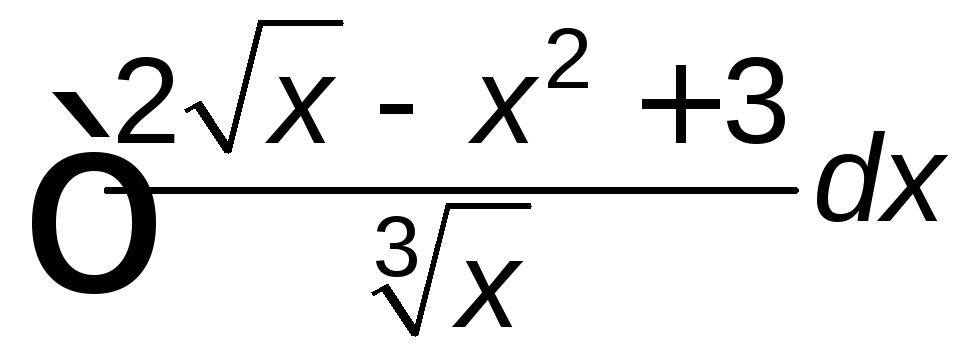 ;
;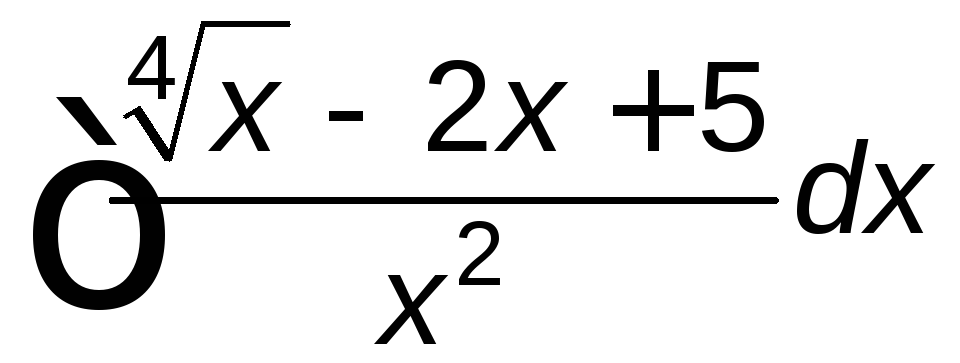 ;
; ;
; ;
;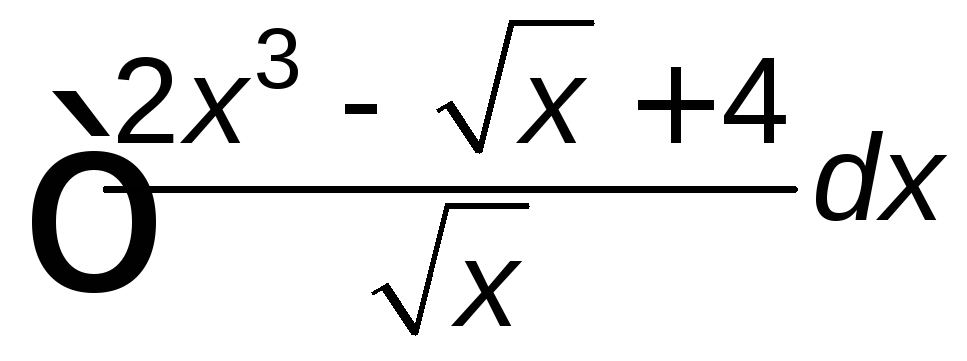 ;
;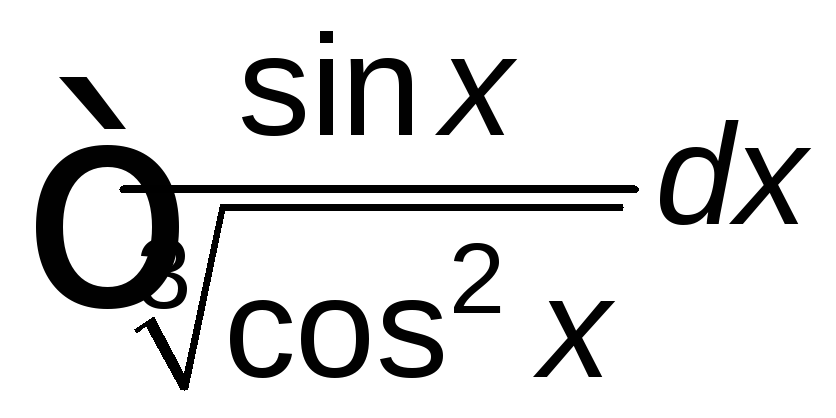 ;
; ;
; ;
;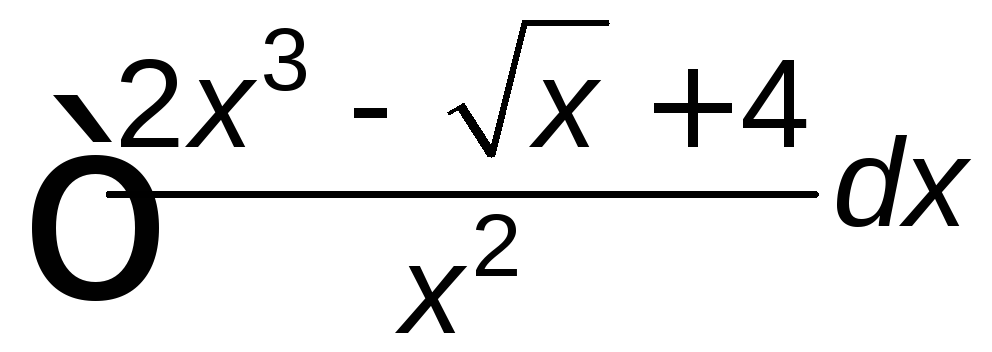 ;
;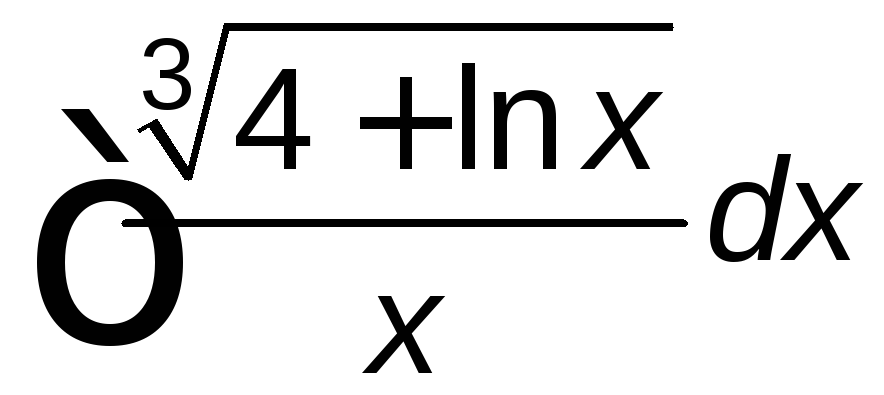 ;
;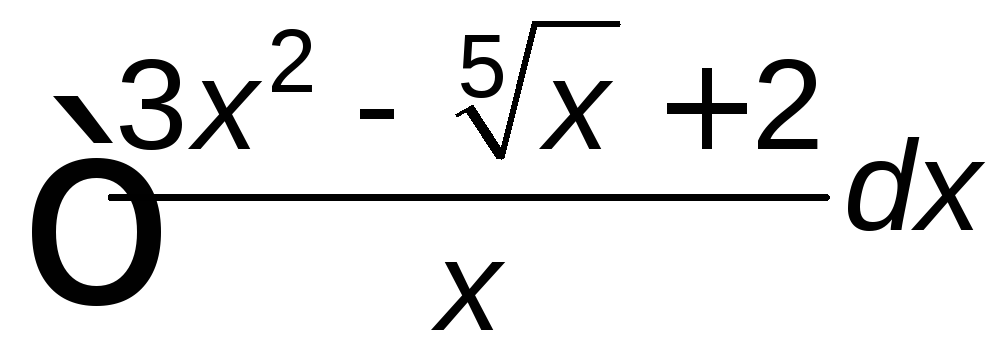 ;
; ;
;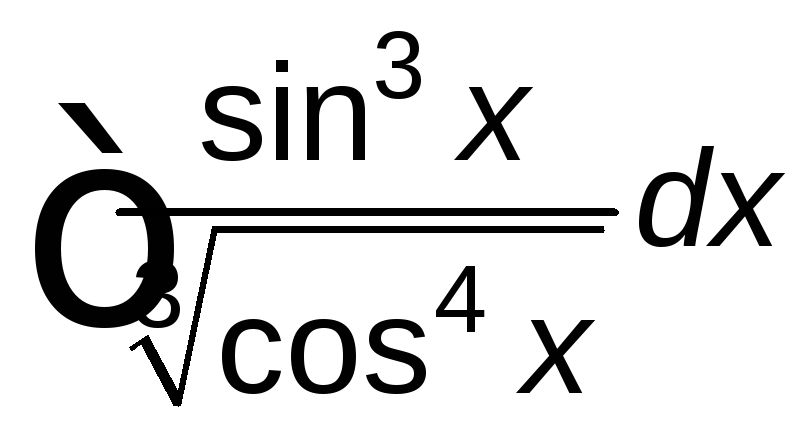 ;
;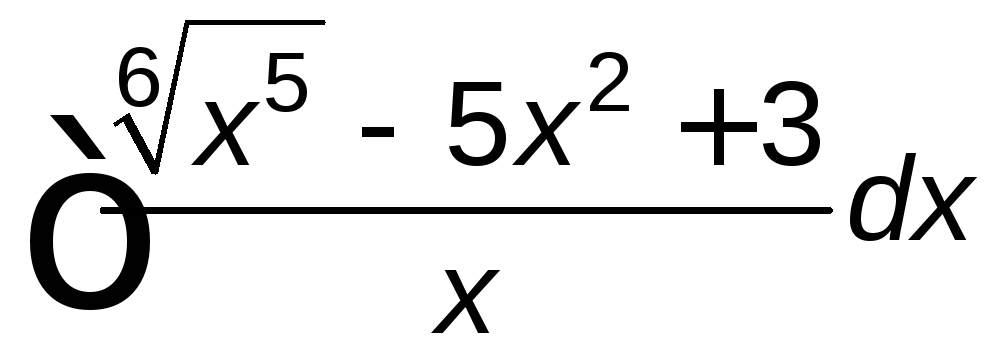 ;
;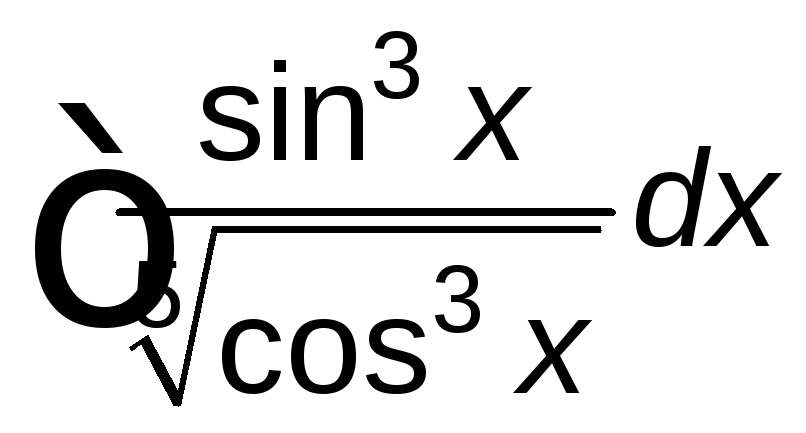 ;
;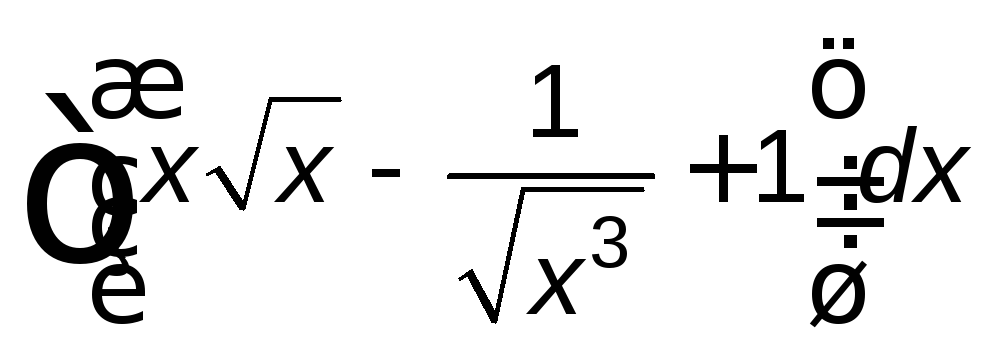 ;
; ;
; ;
;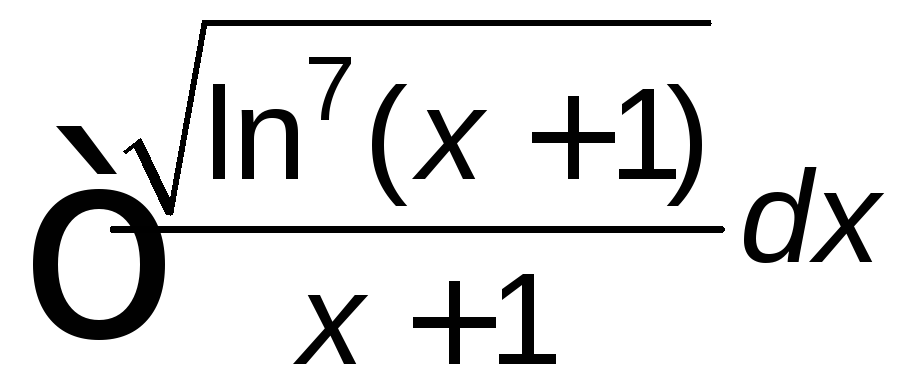 ;
; ;
;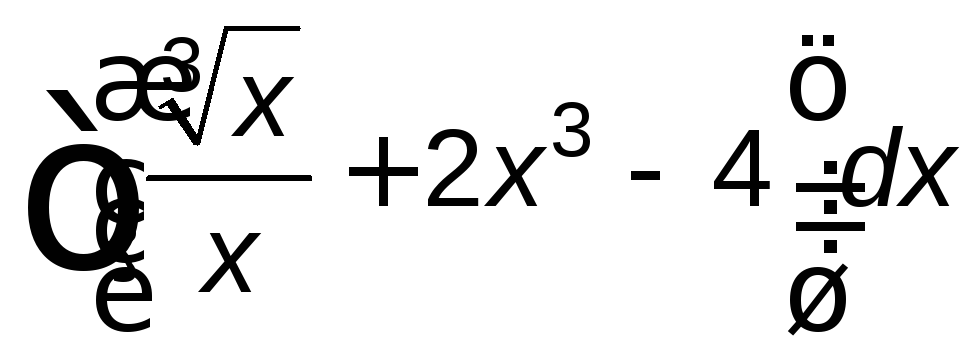 ;
;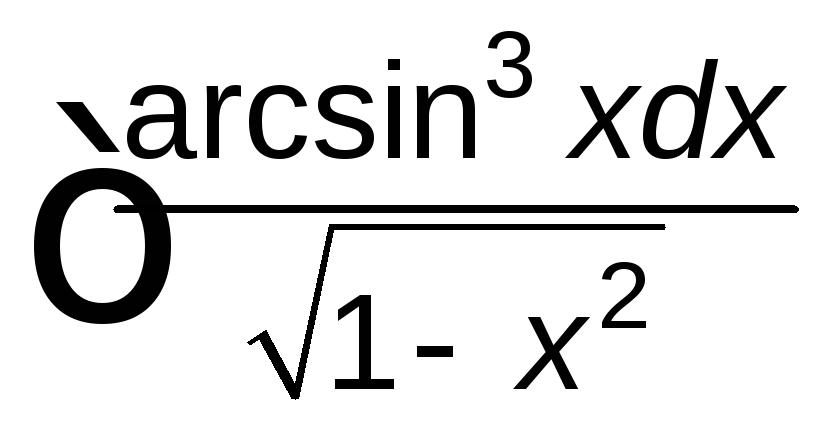 ;
;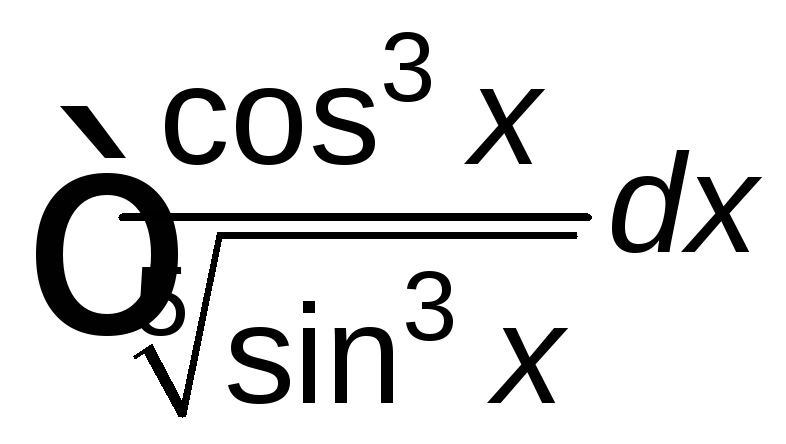 ;
;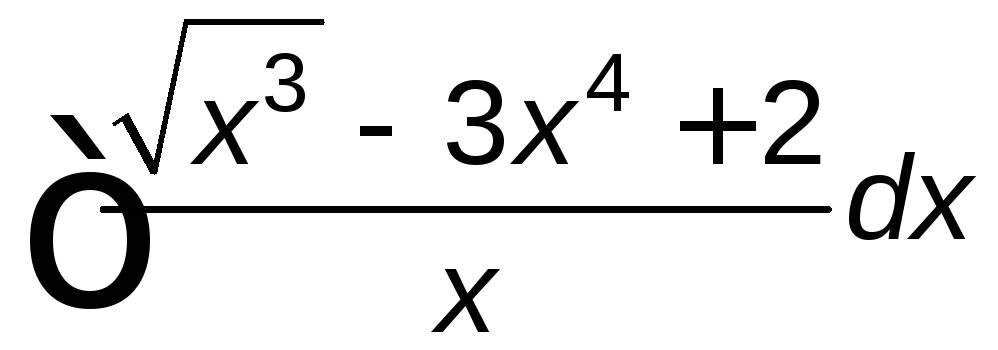 ;
;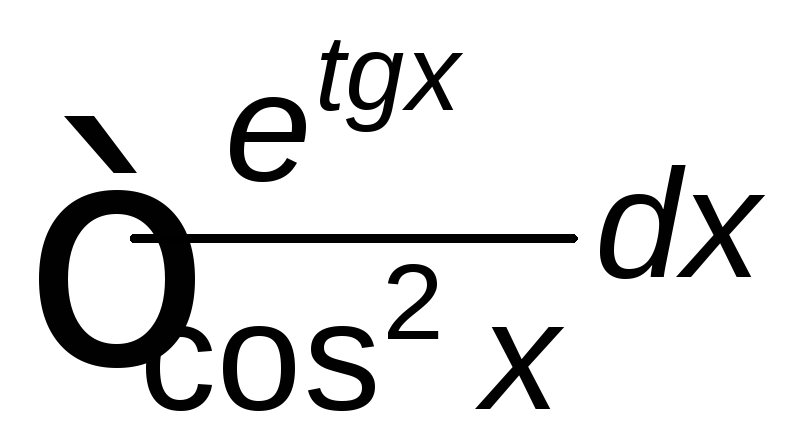 ;
;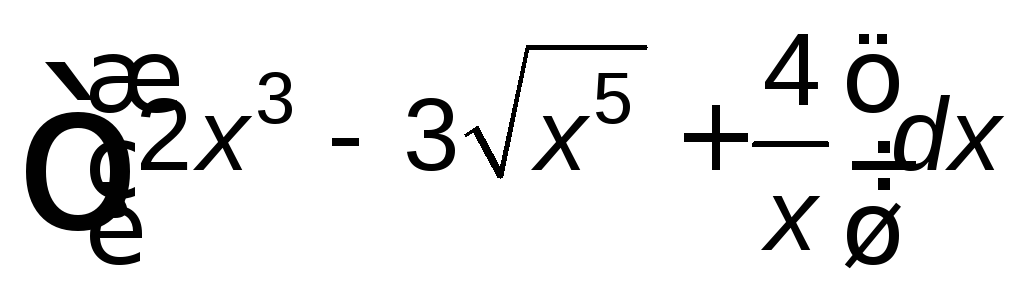 ;
;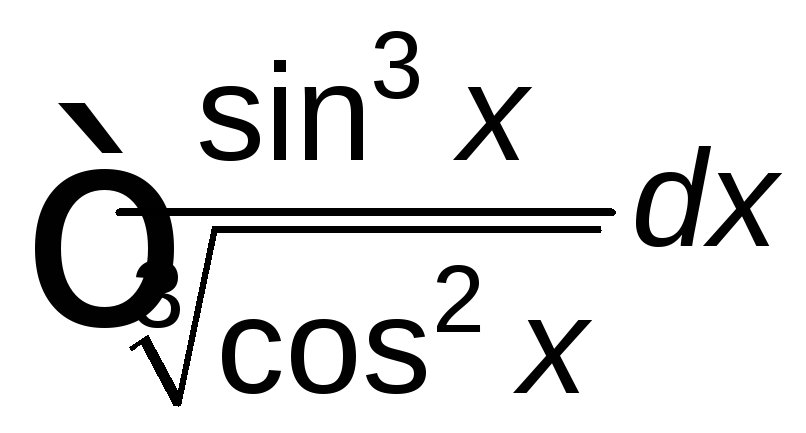 ;
;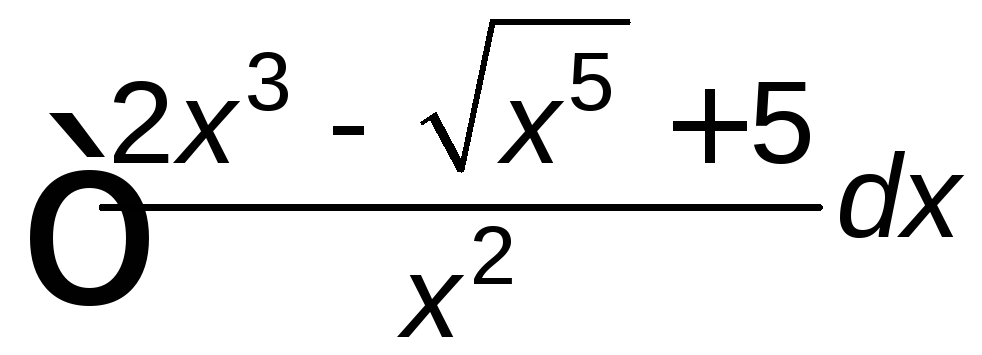 ;
;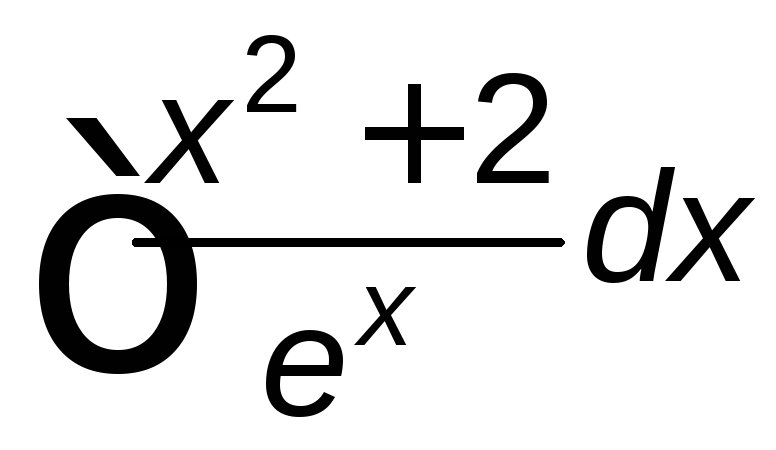 ;
; ;
; ;
; ;
;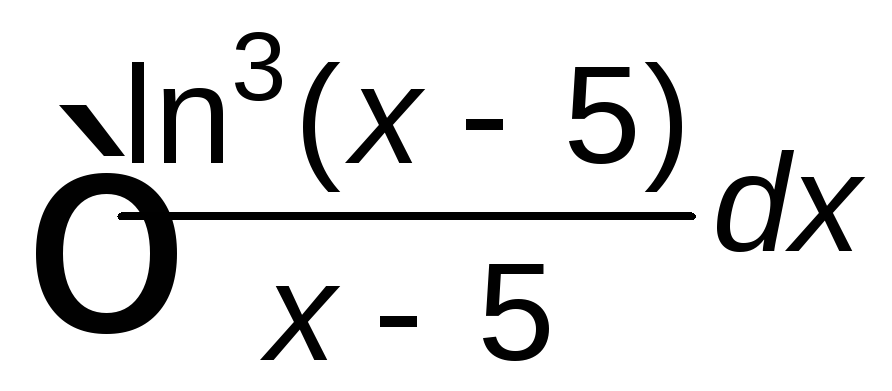 ;
; ;
;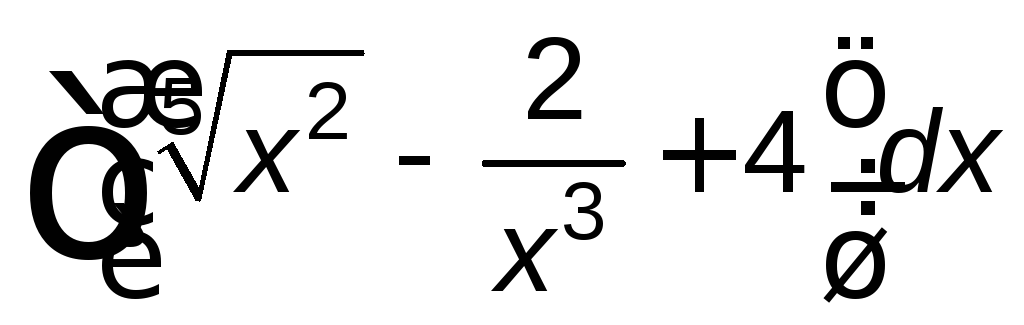 ;
;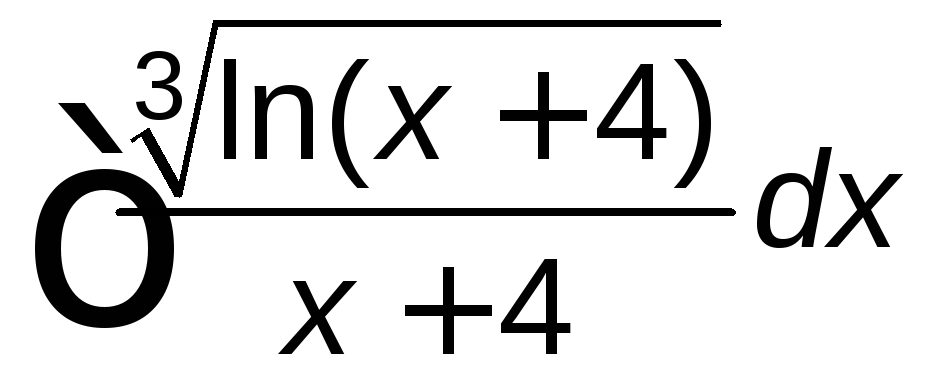 ;
; ;
; ;
; ;
;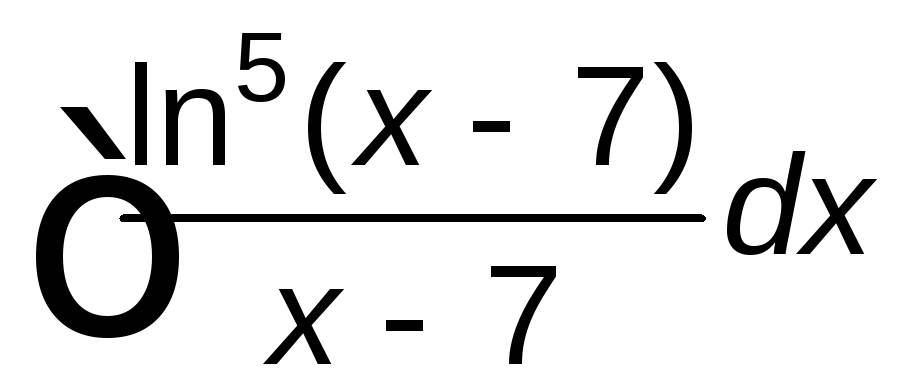 ;
;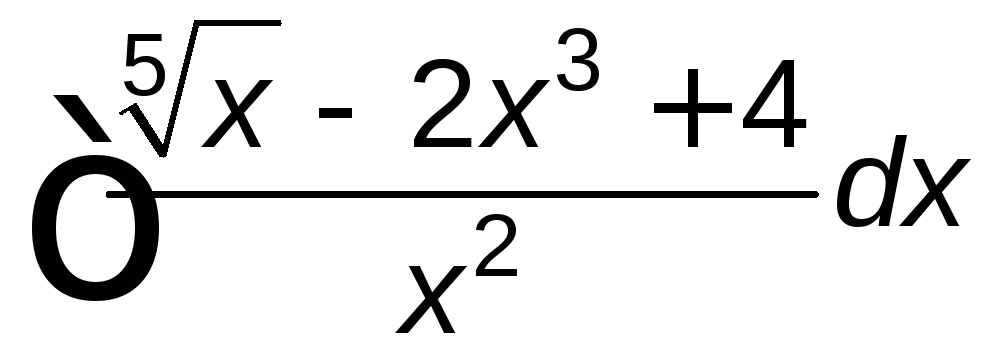 ;
; ;
; ;
;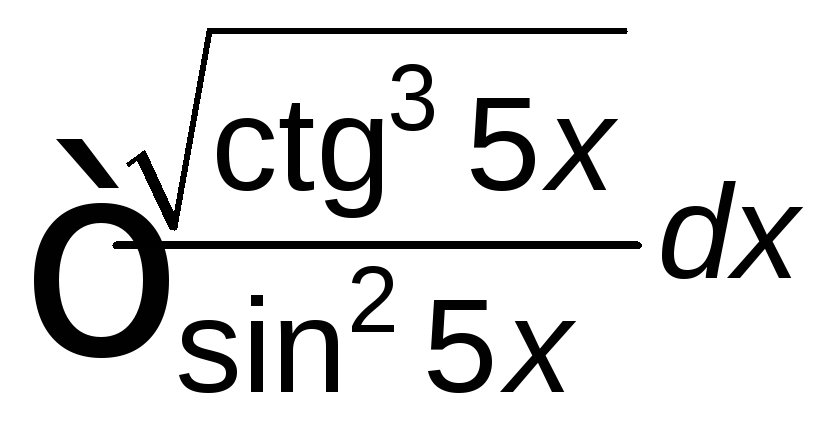 ;
;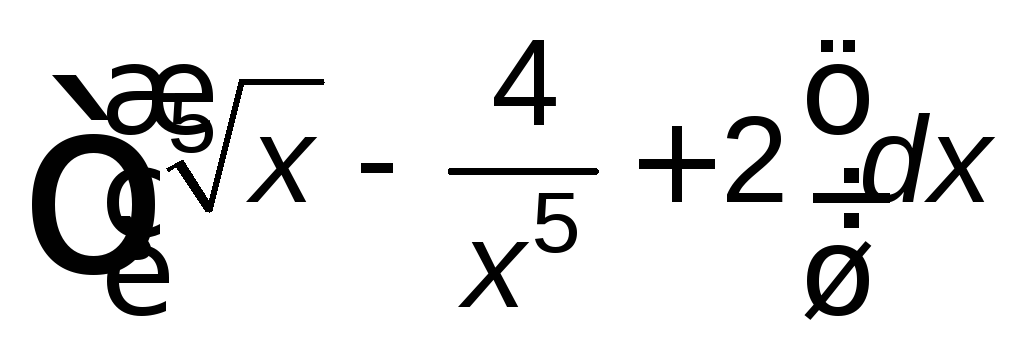 ;
;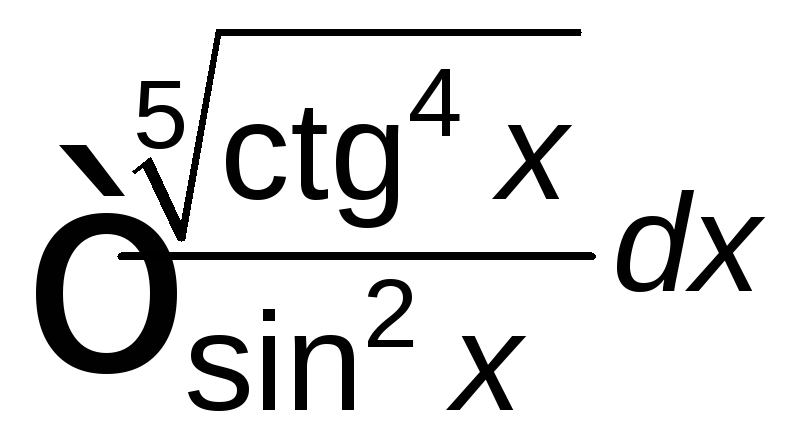 ;
;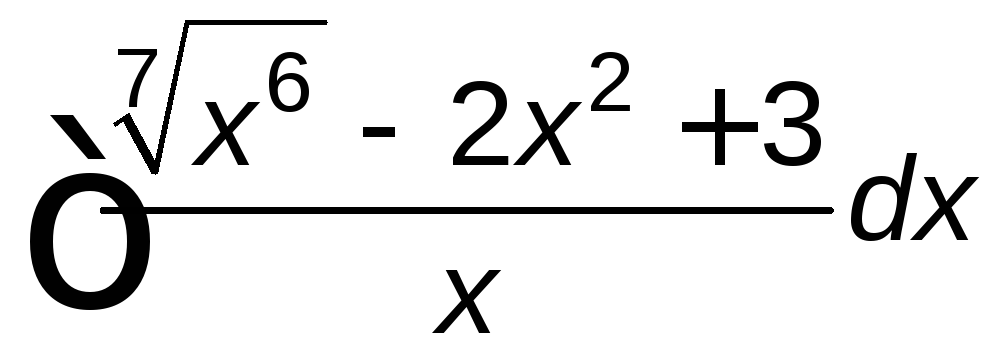 ;
; ;
;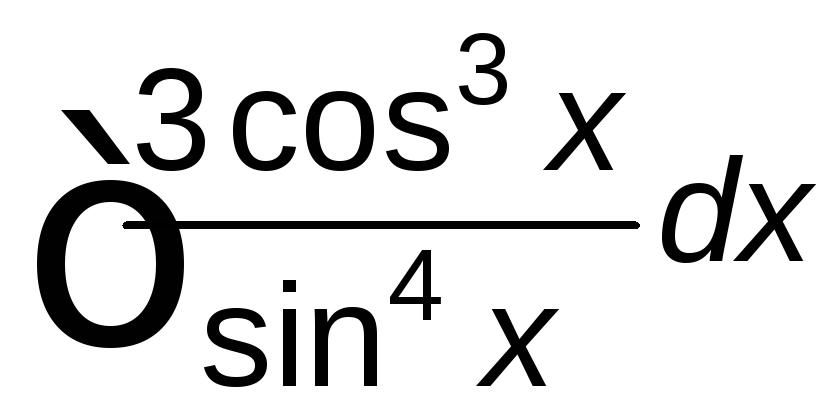 ;
;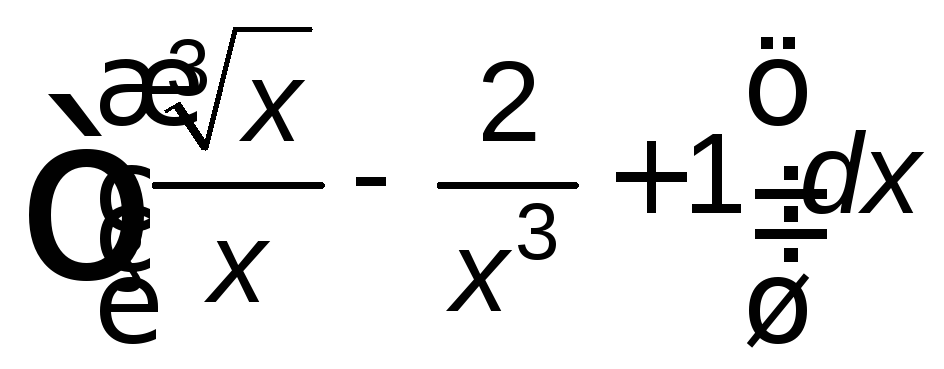 ;
;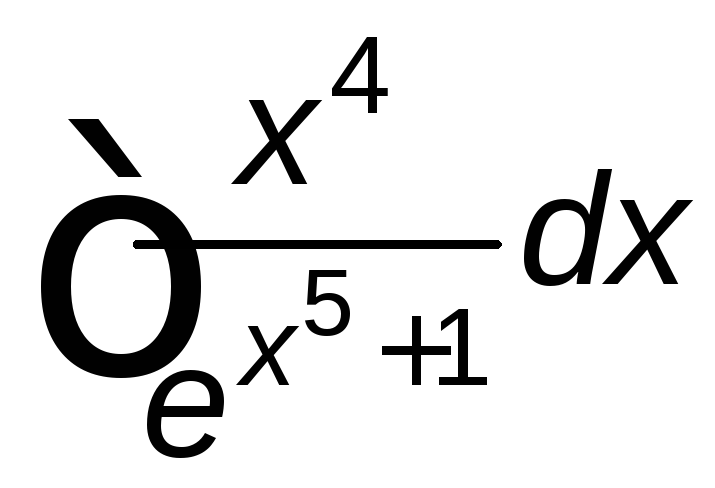 ;
;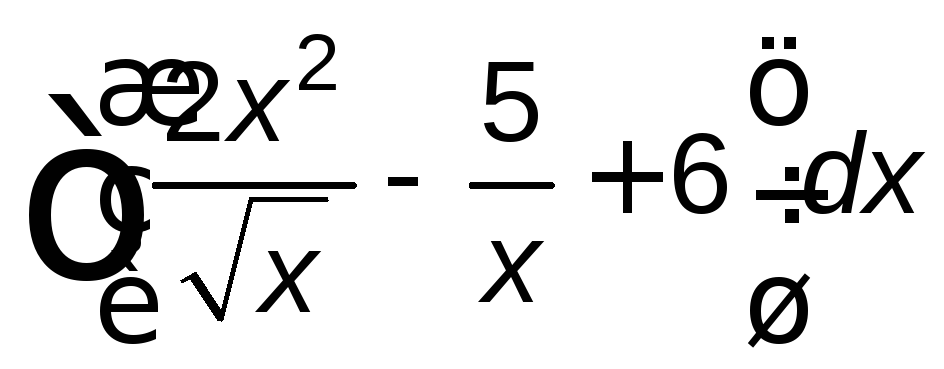 ;
;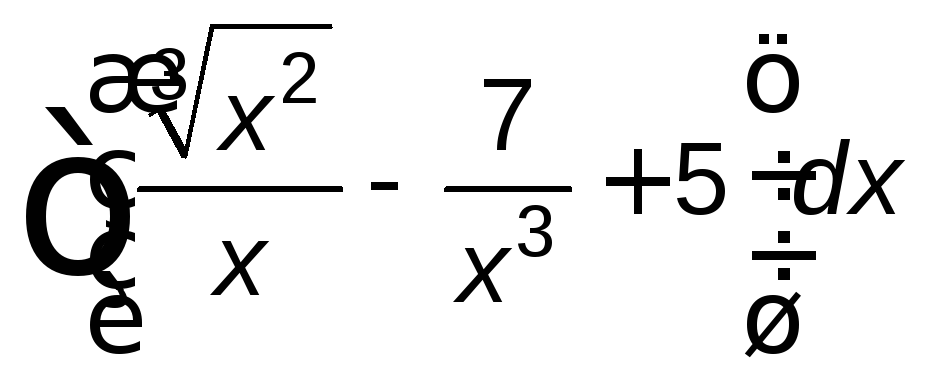 ;
; ;
;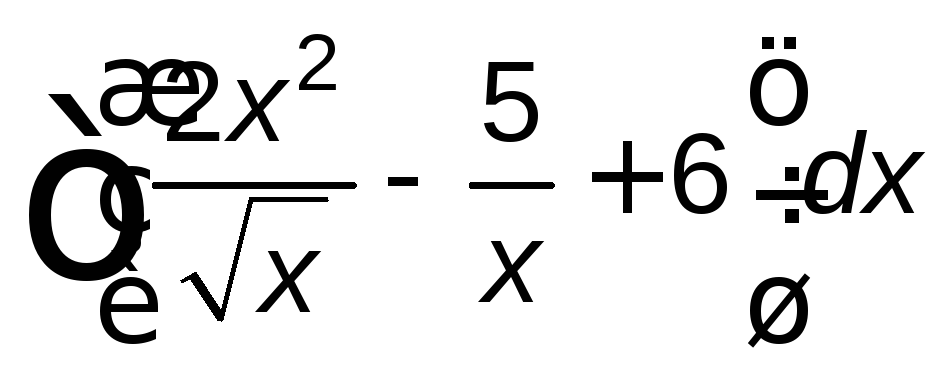 ;
;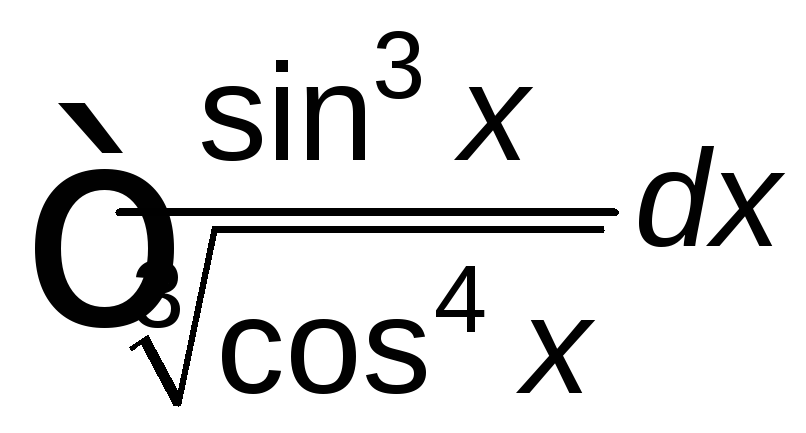 ;
;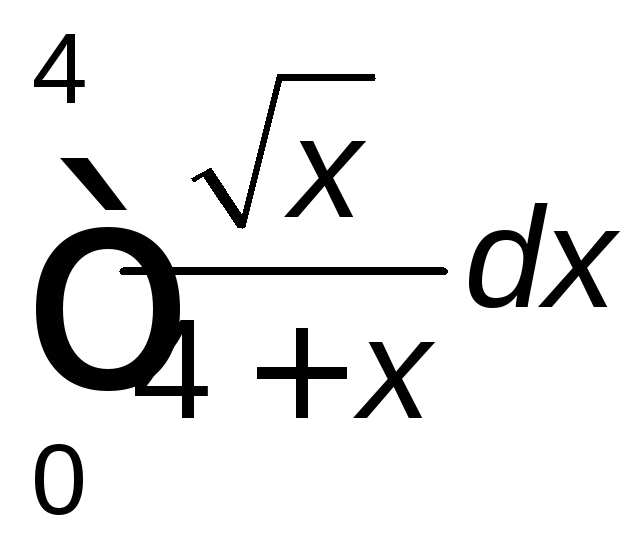 .
.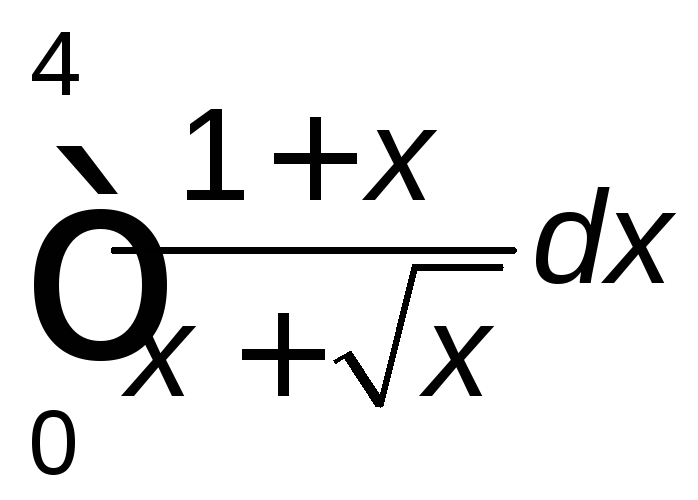 .
.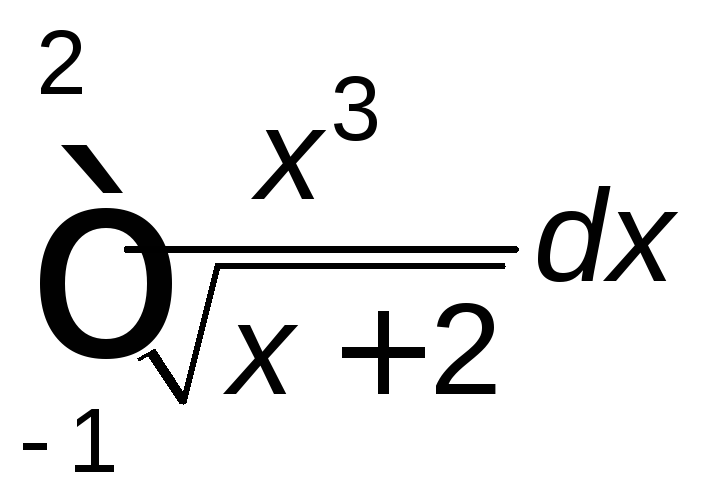 .
.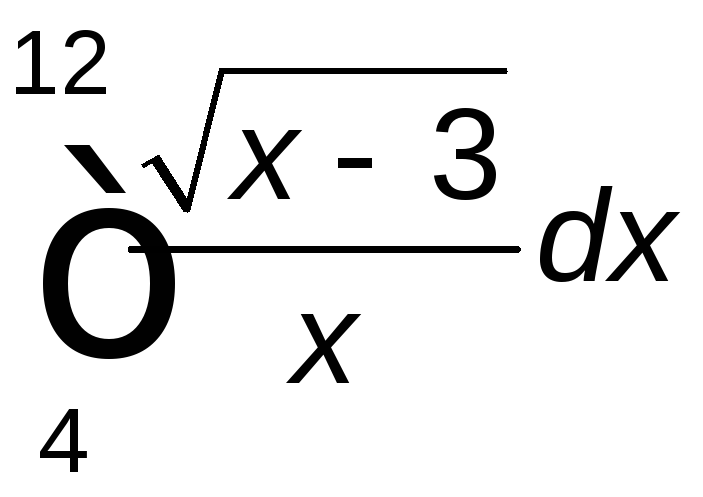 .
. .
.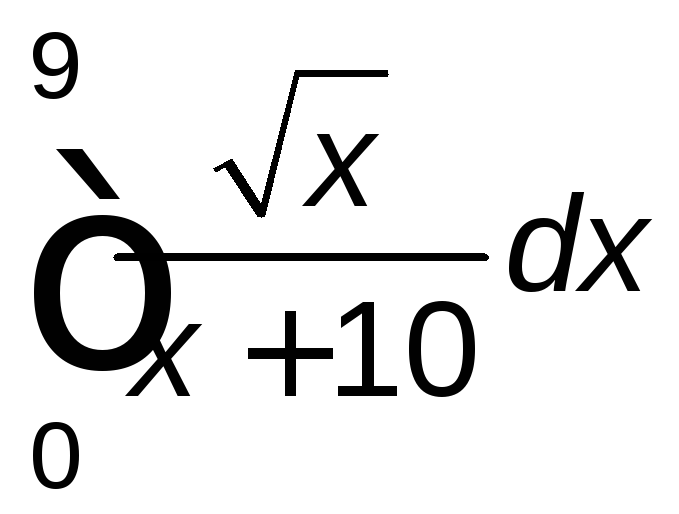 .
.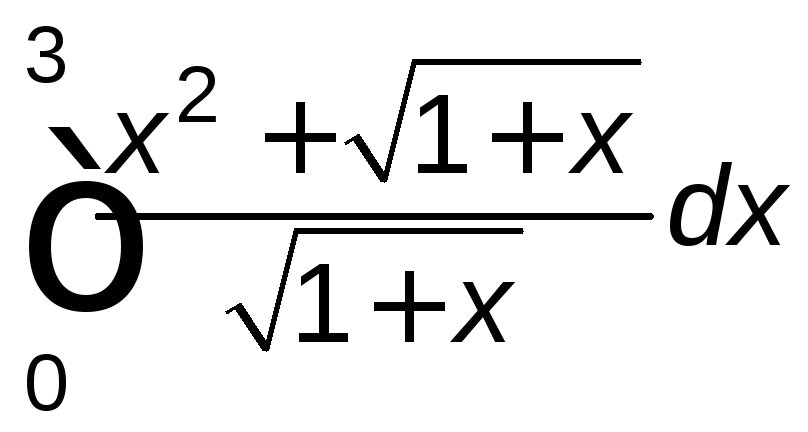 .
.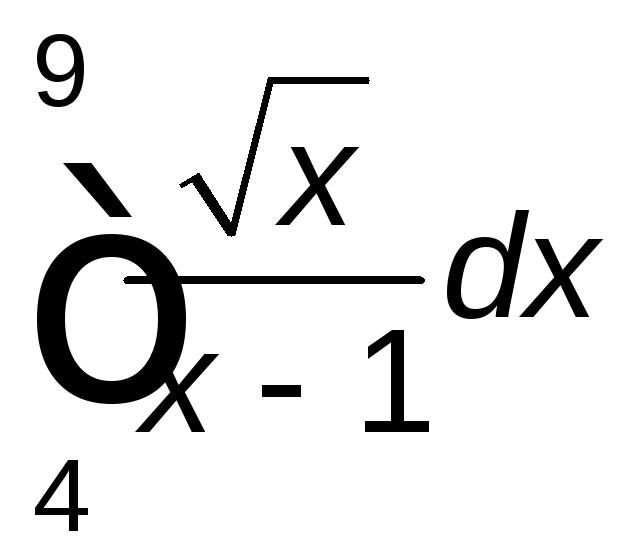 .
.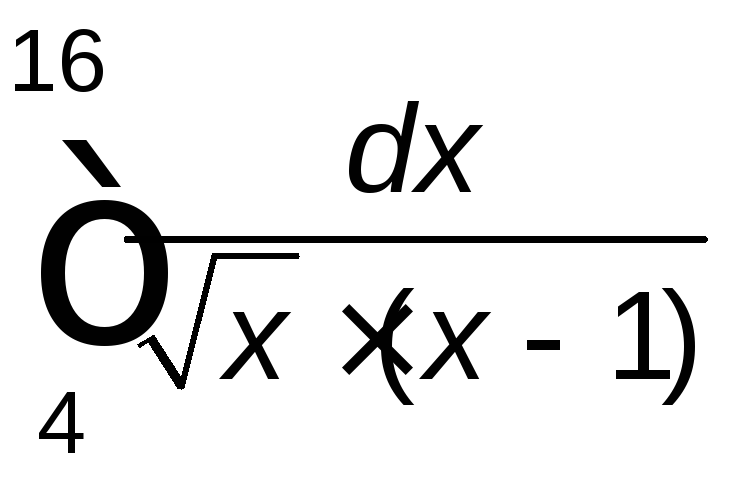 .
.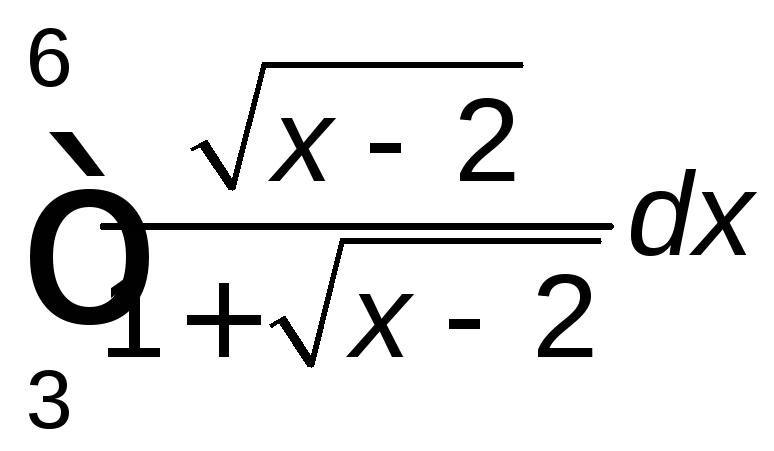 .
. .
.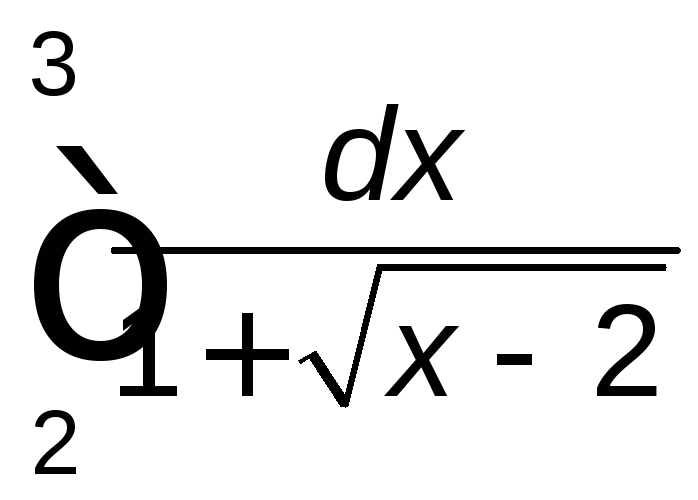 .
.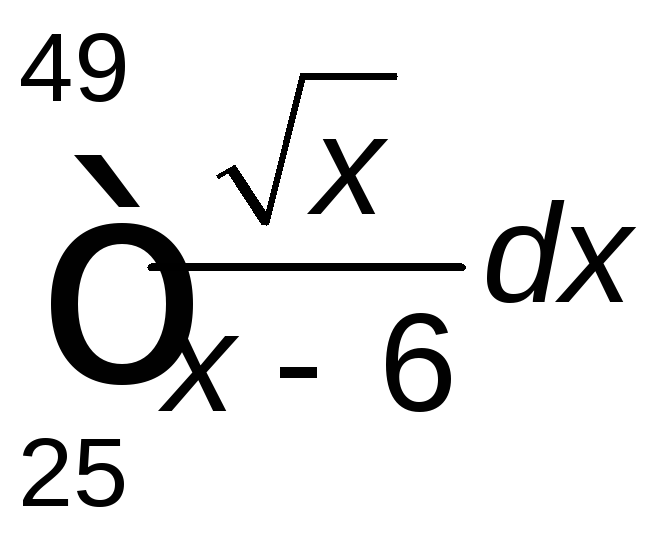 .
.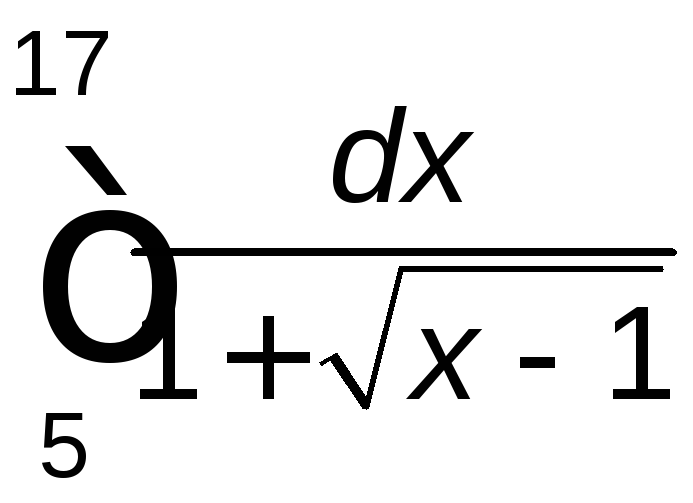 .
.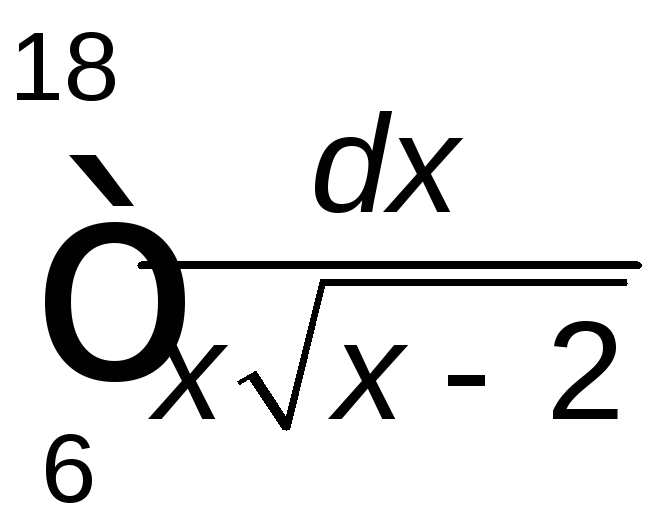 .
.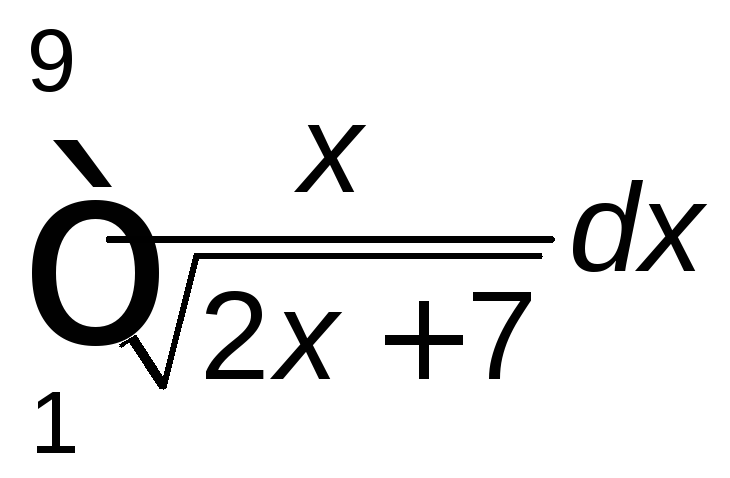 .
. .
.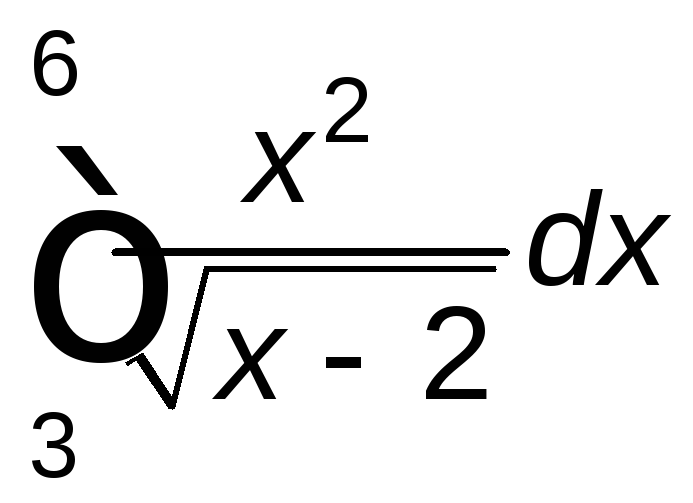 .
.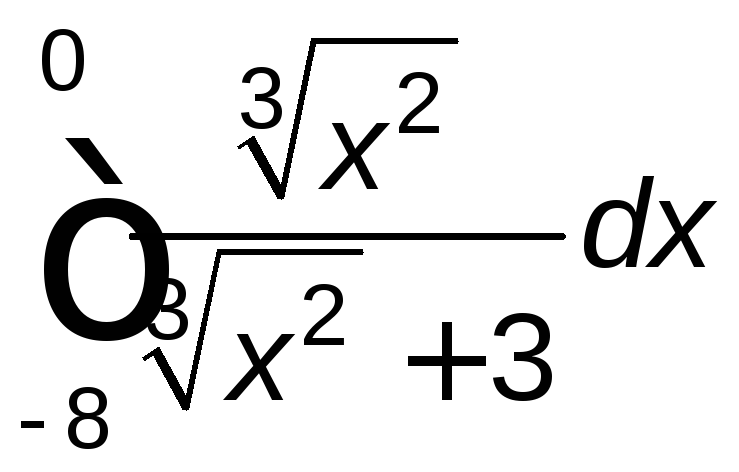 .
.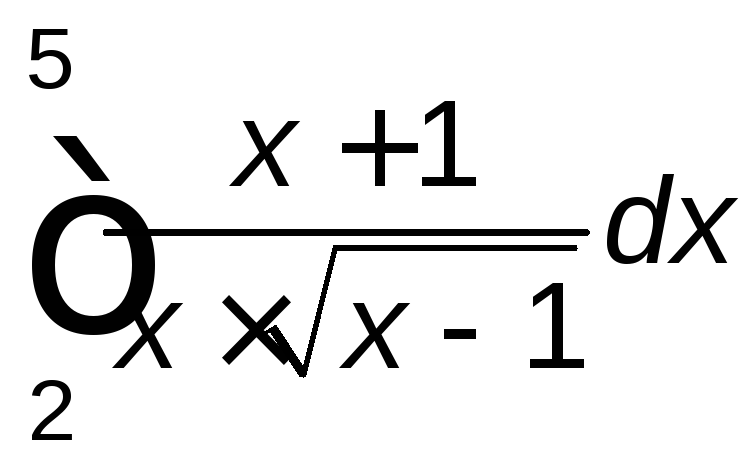 .
. .
.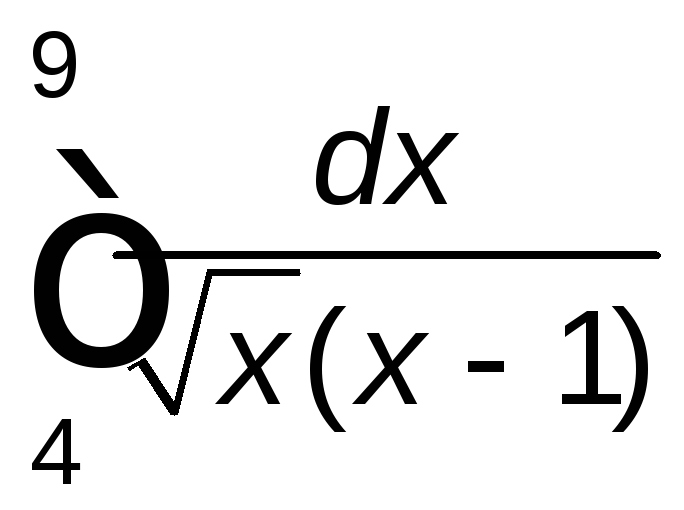 .
.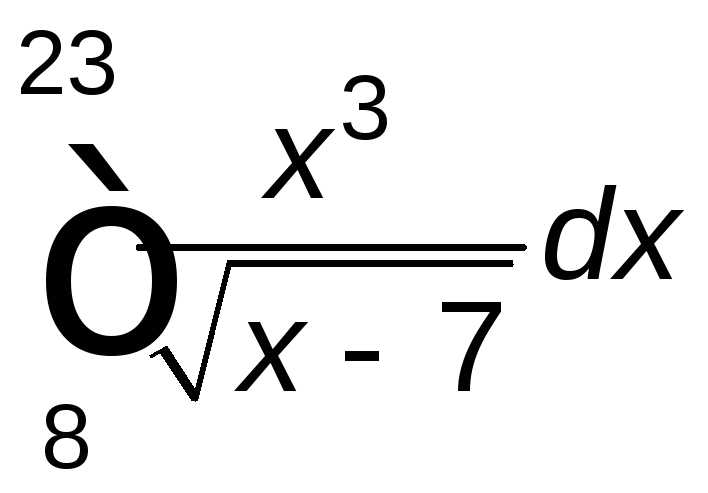 .
.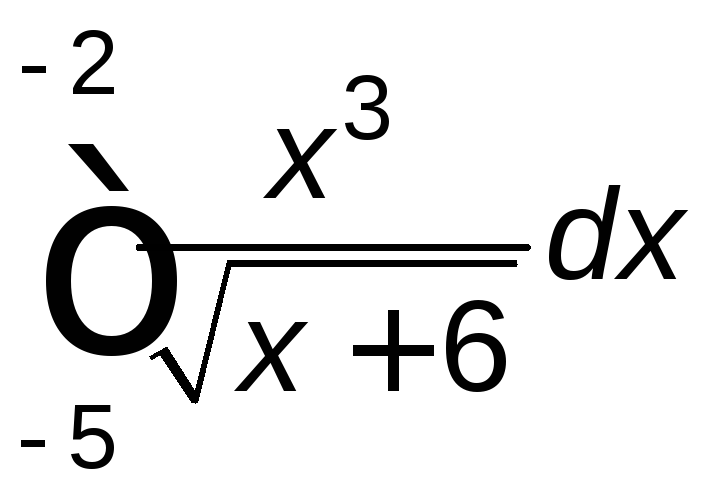 .
.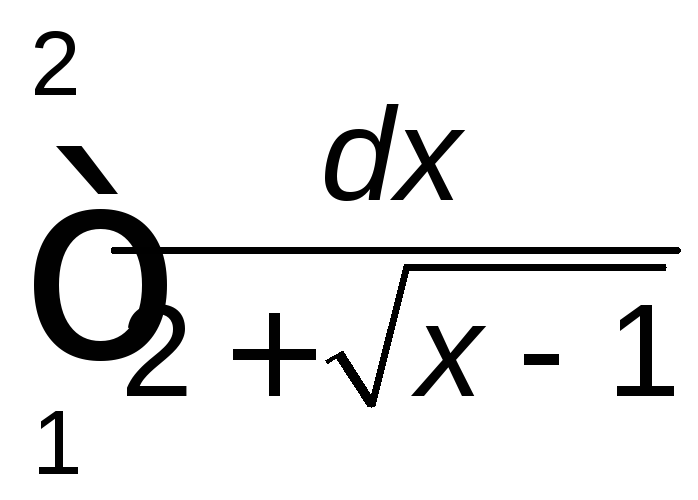 .
. .
. .
.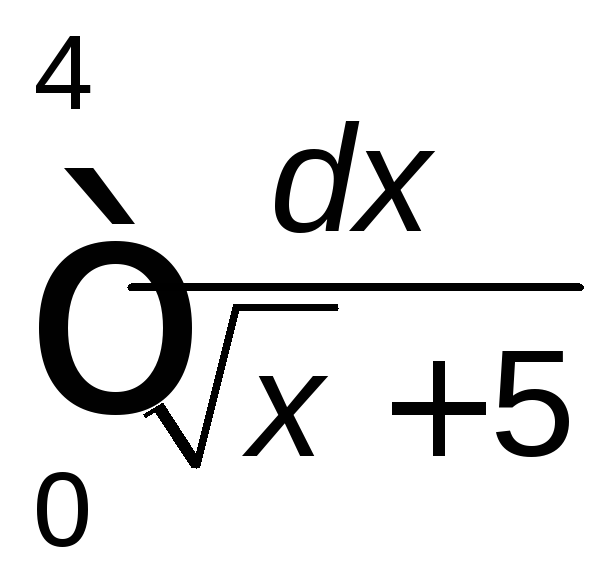 .
. .
.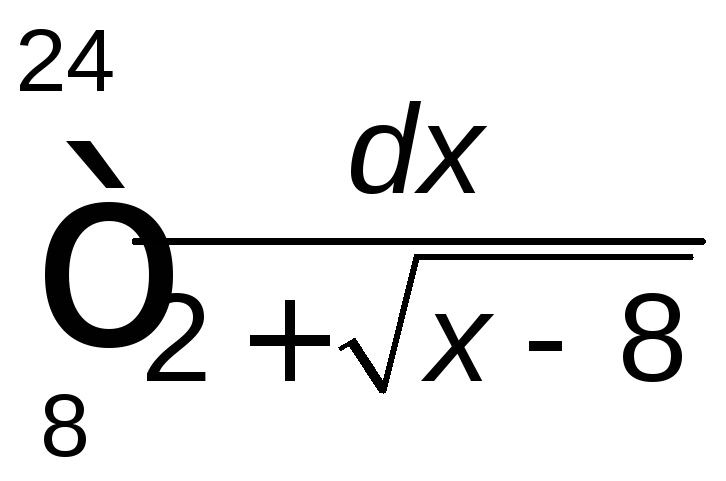 .
. .
.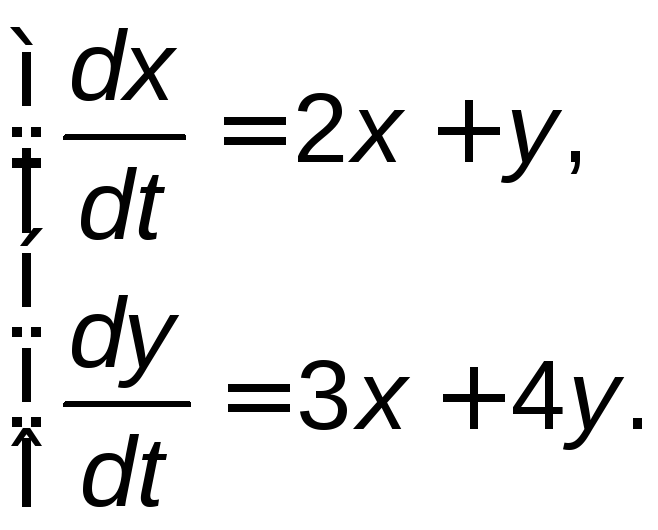


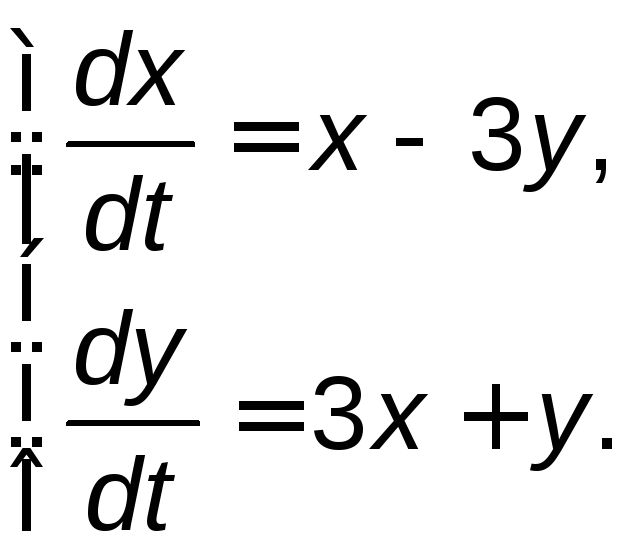
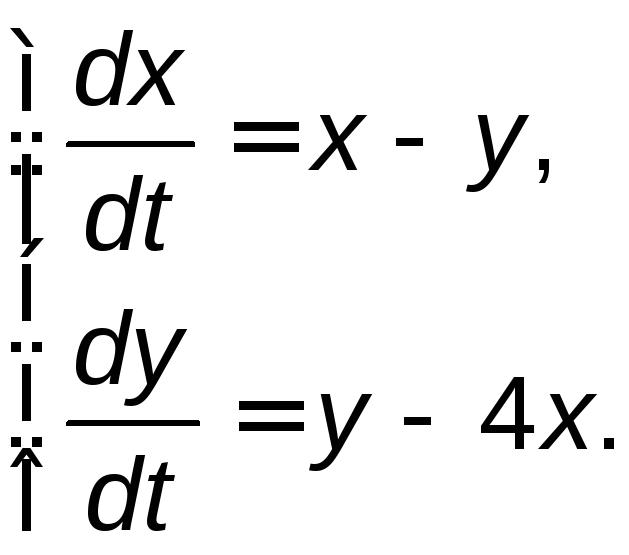
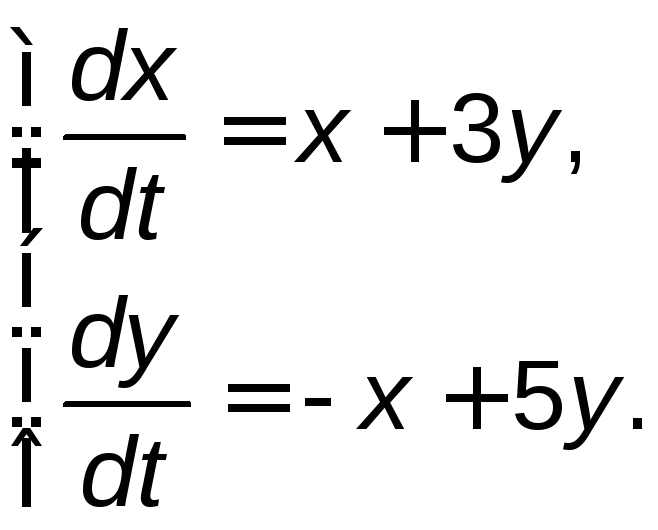
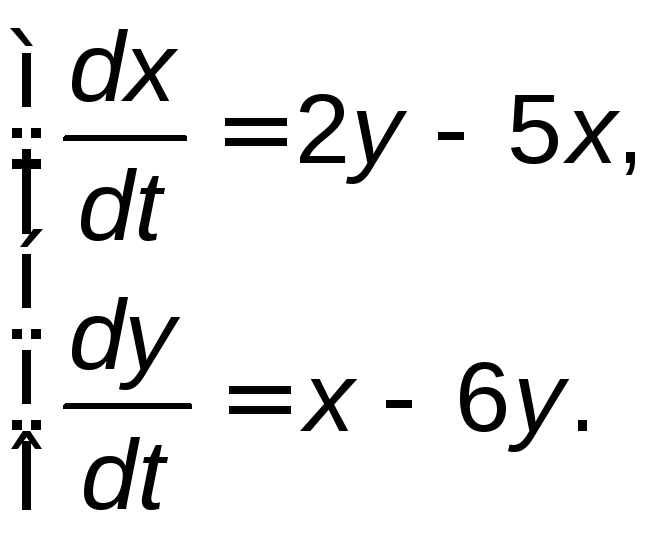
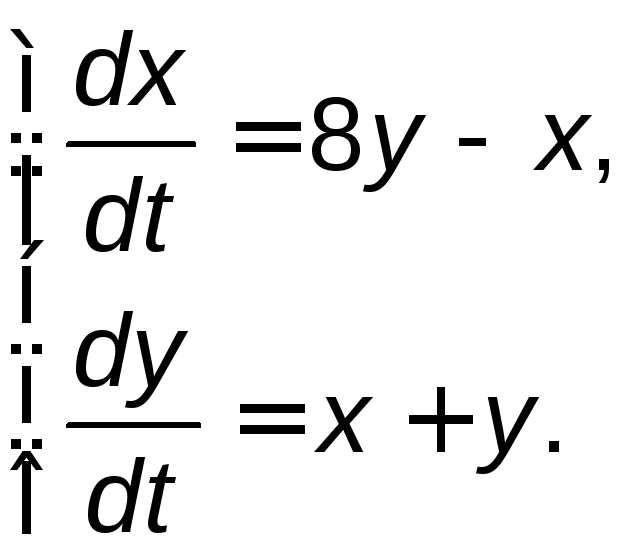

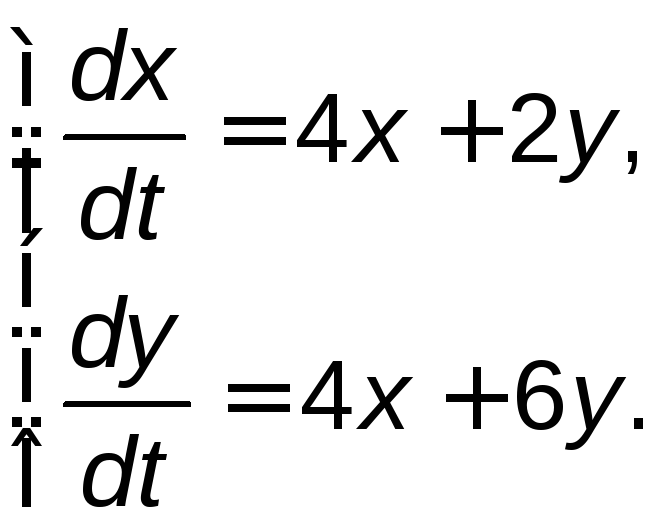


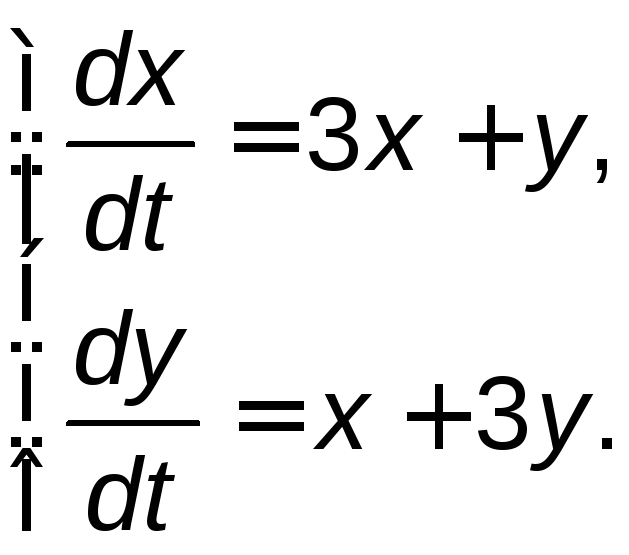
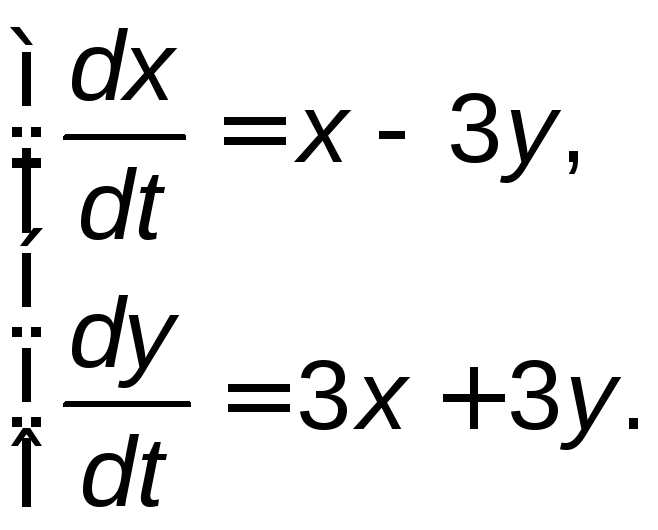
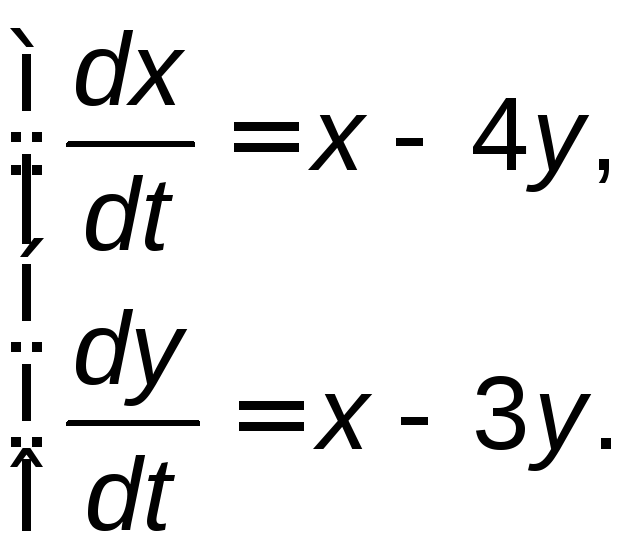
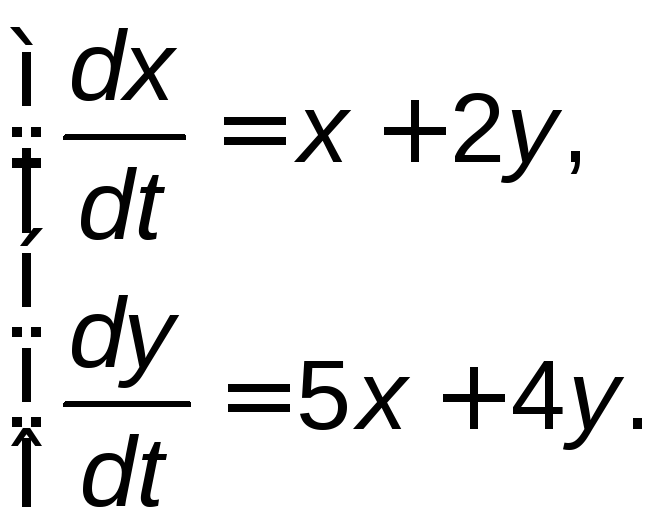
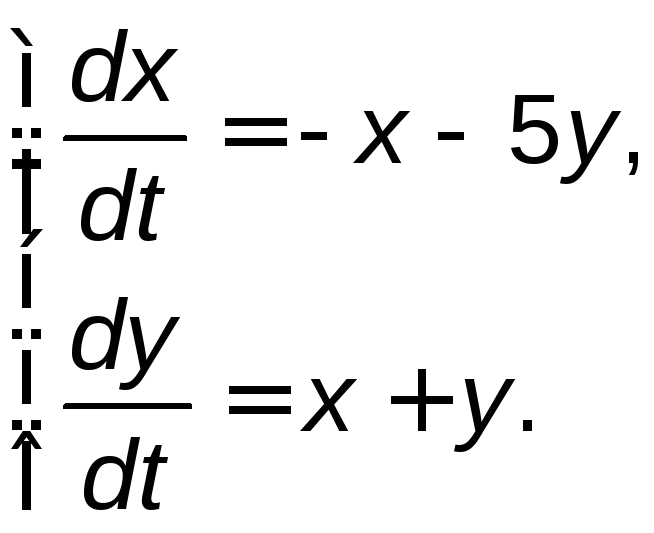
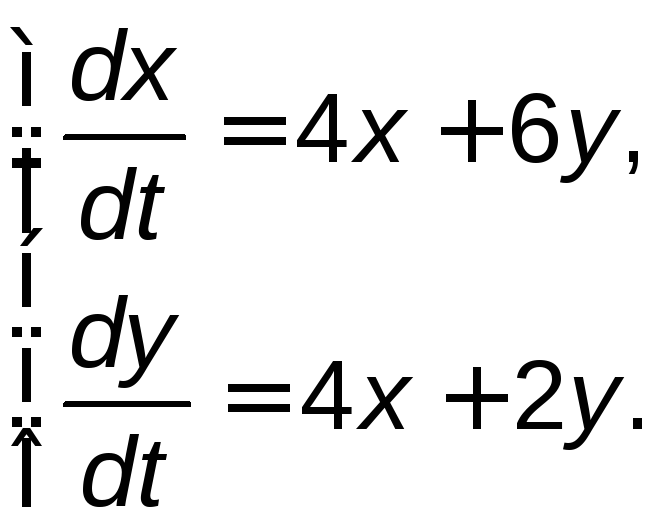
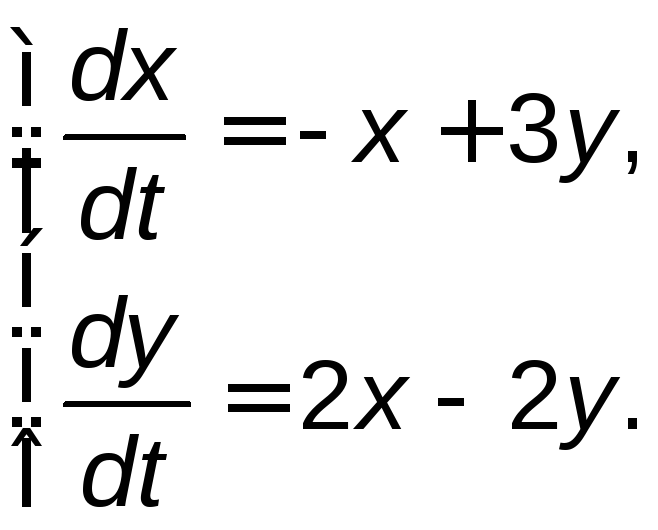
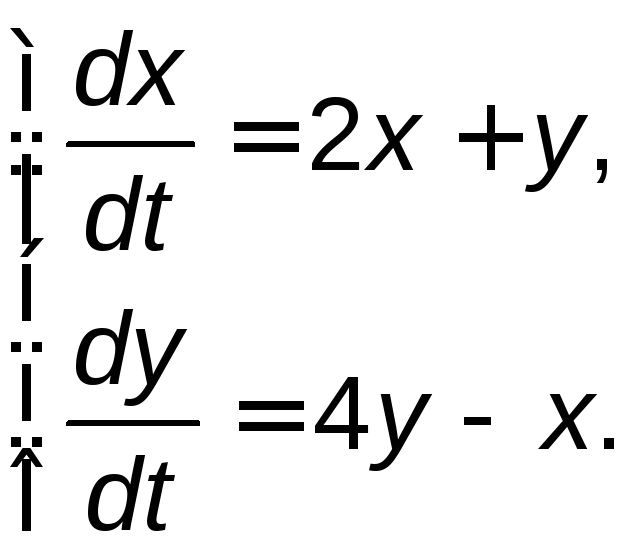
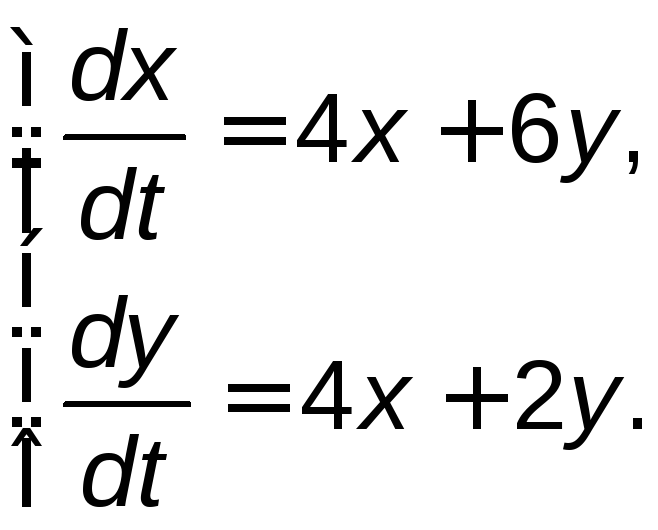
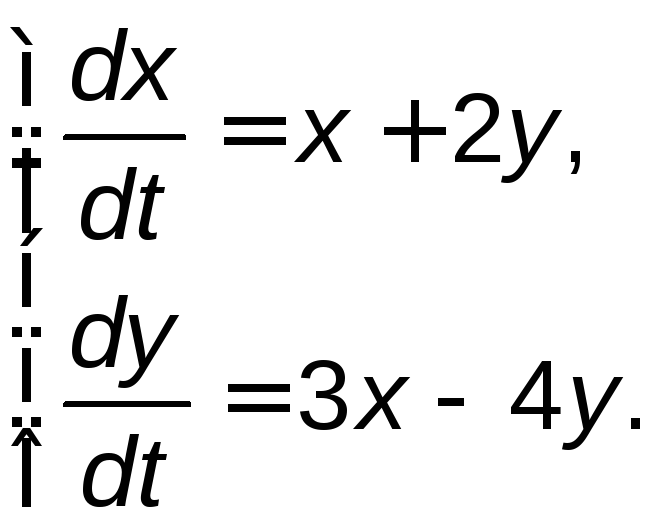
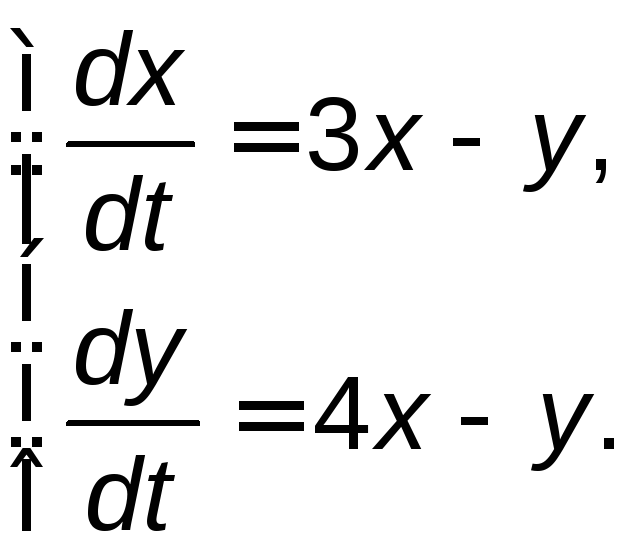
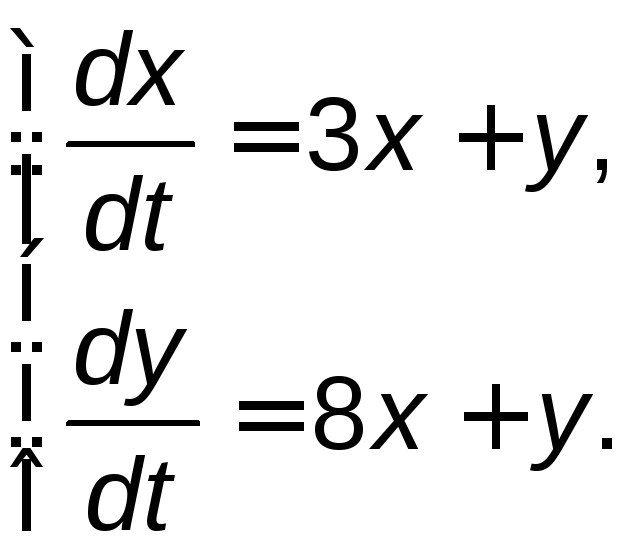


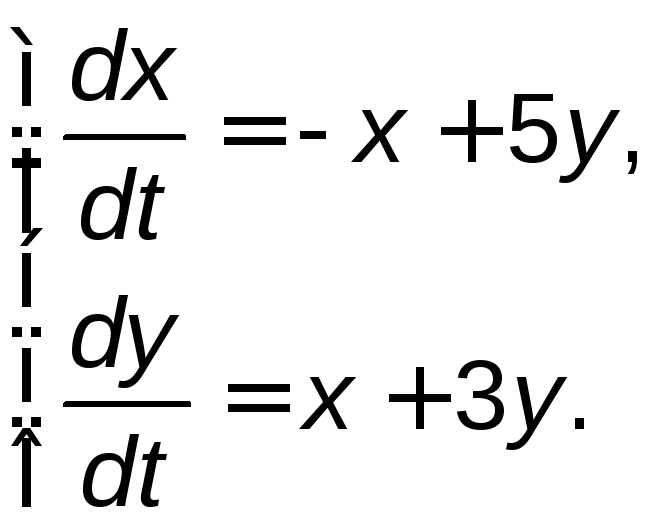
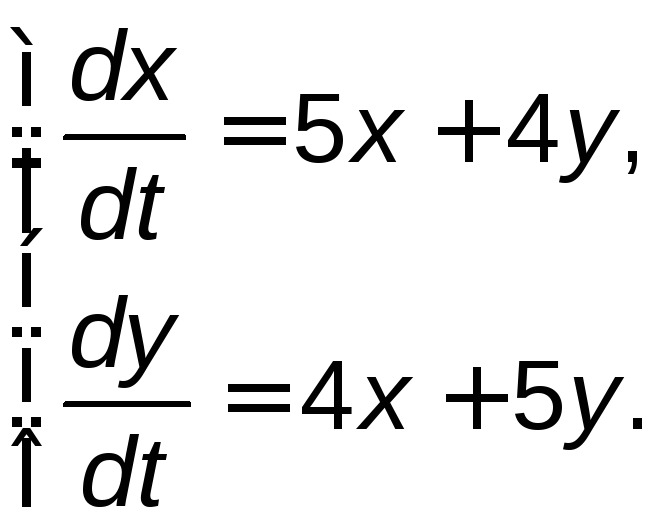
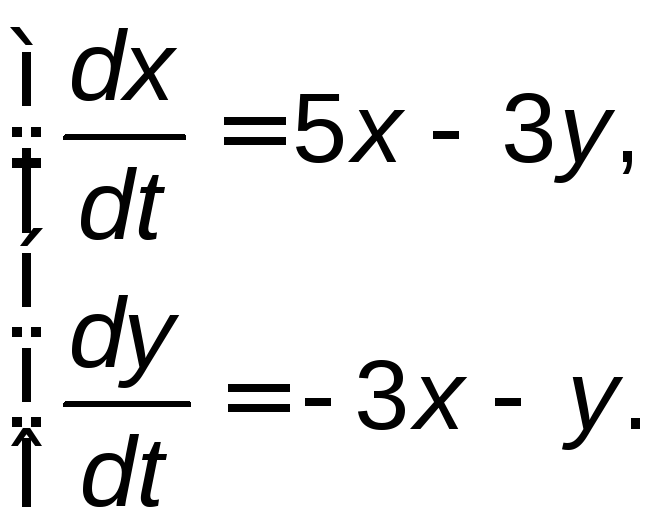
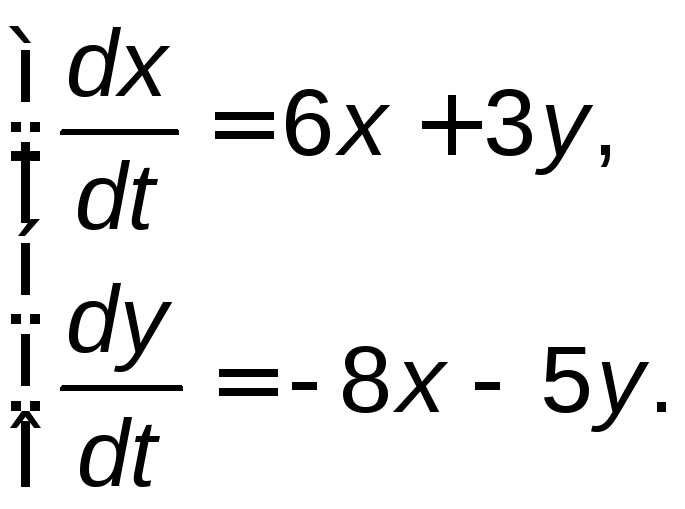
 ,
,
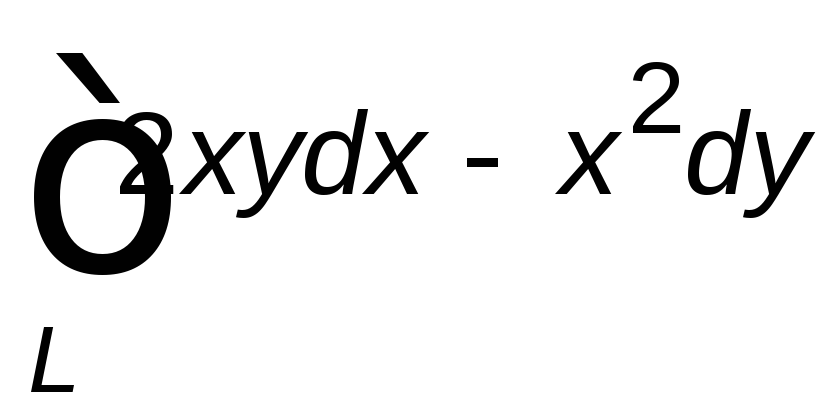 ,
,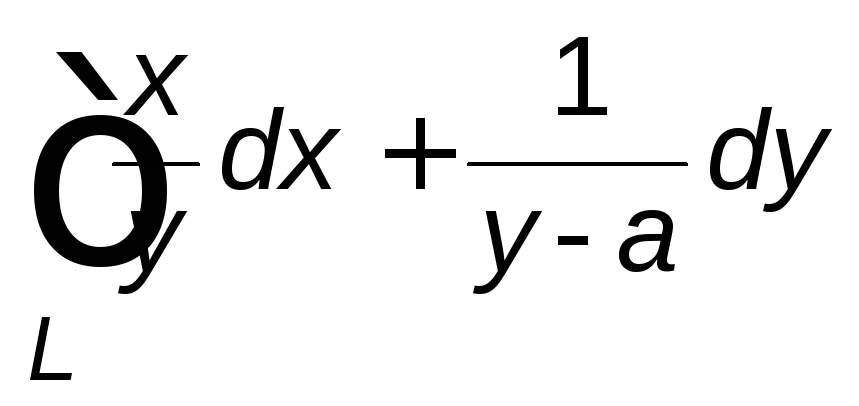 ,
,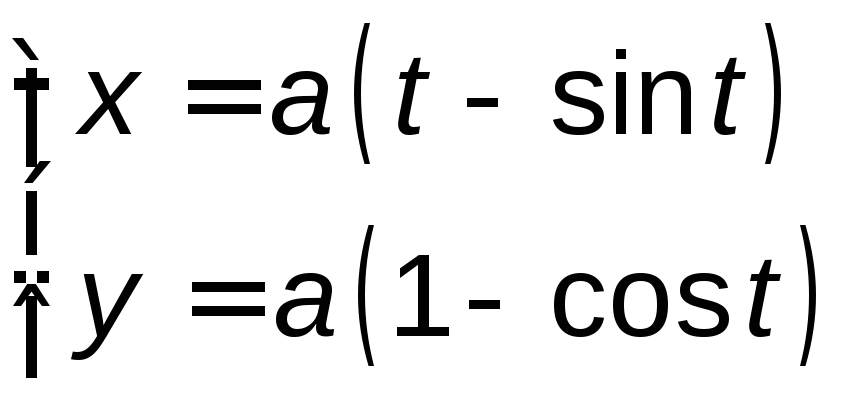 ,
при
,
при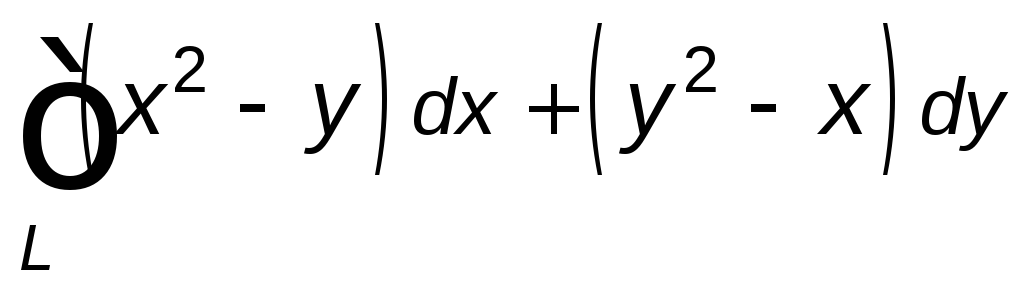 ,
,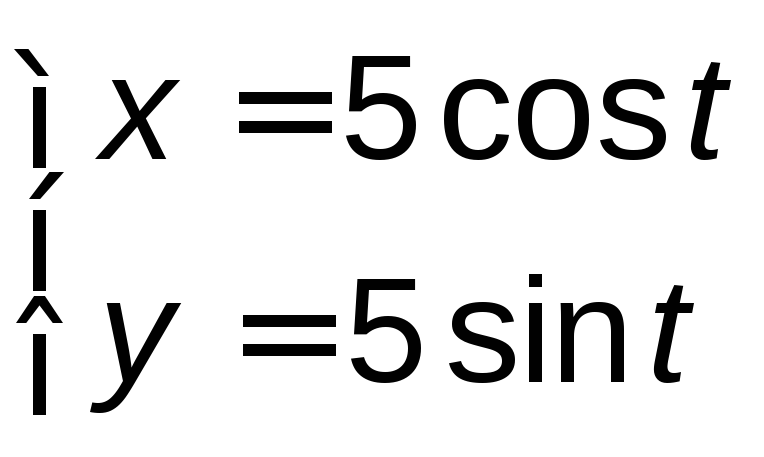 ,
от точки
,
от точки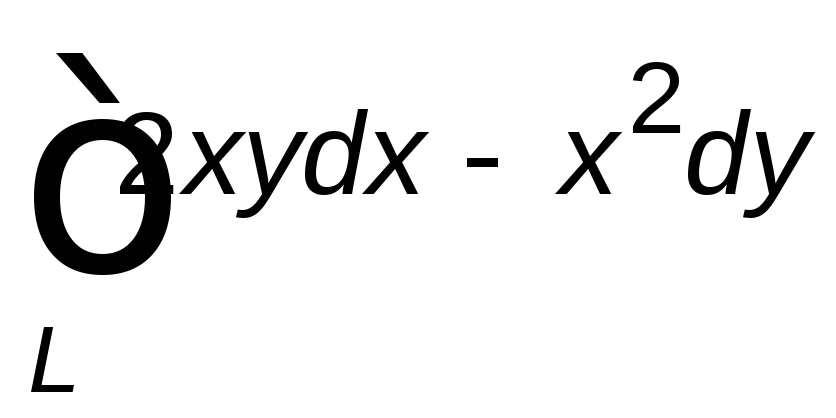 ,
,
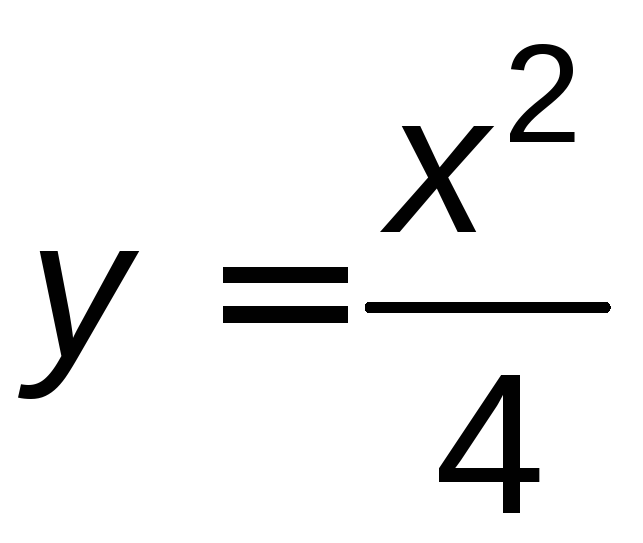 от точки
от точки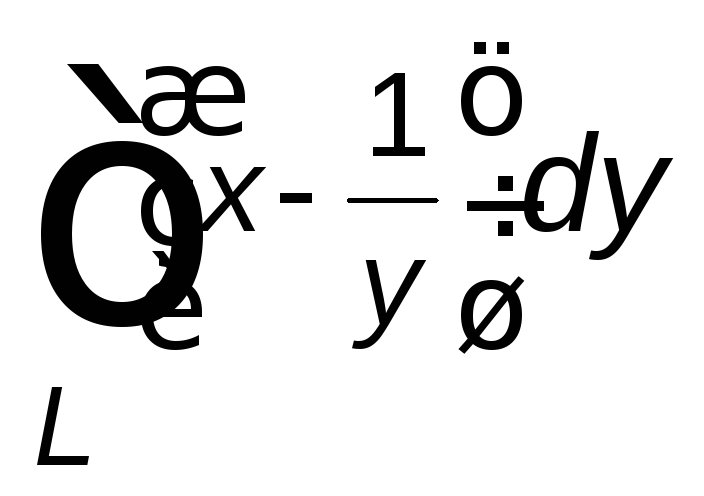 ,
,
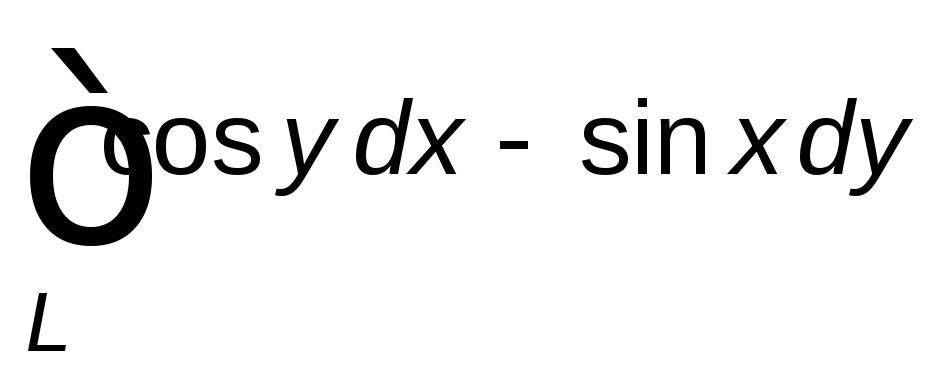 ,
,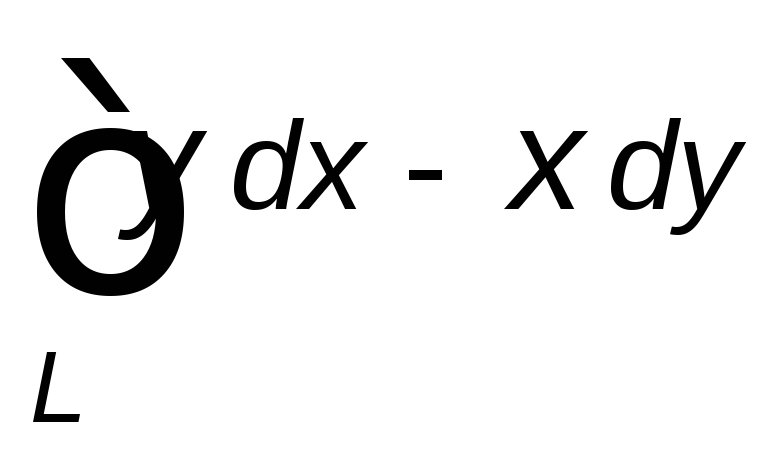 ,
,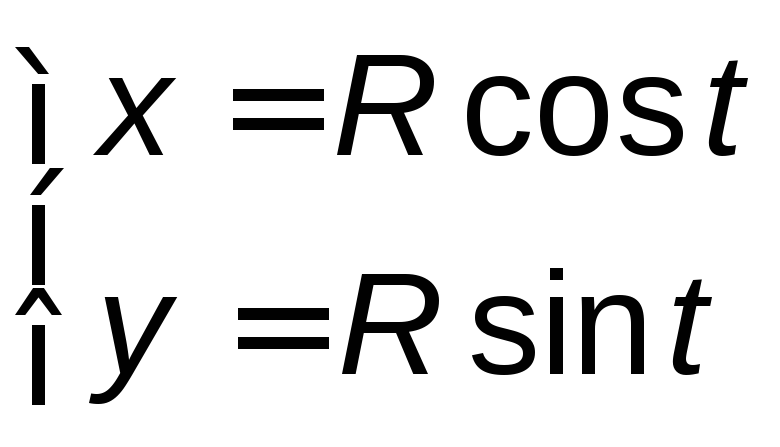 ,
лежащая в первом квадранте и «пробегаемая»
против хода часовой стрелки.
,
лежащая в первом квадранте и «пробегаемая»
против хода часовой стрелки. ,
,
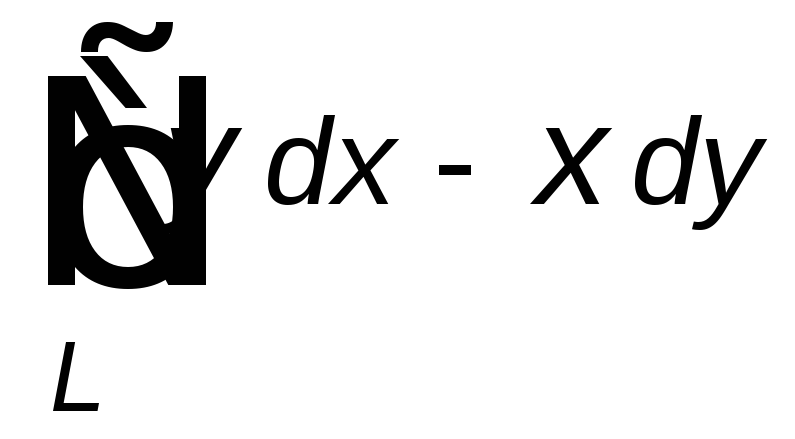 ,
,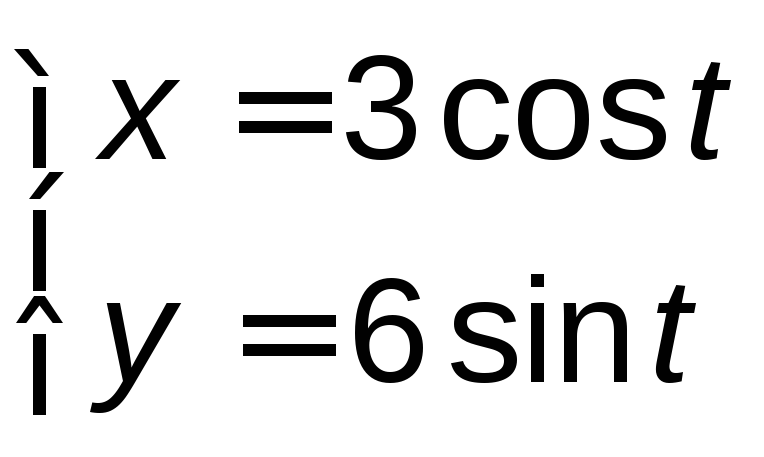 ,
«пробегаемая» против хода часовой
стрелки.
,
«пробегаемая» против хода часовой
стрелки.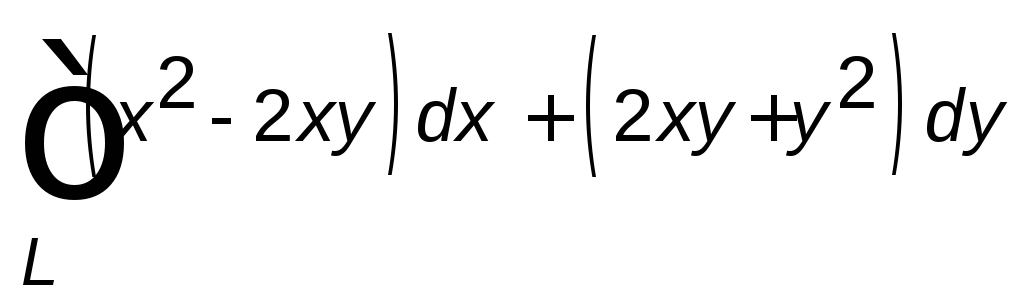 ,
,
 ,
,
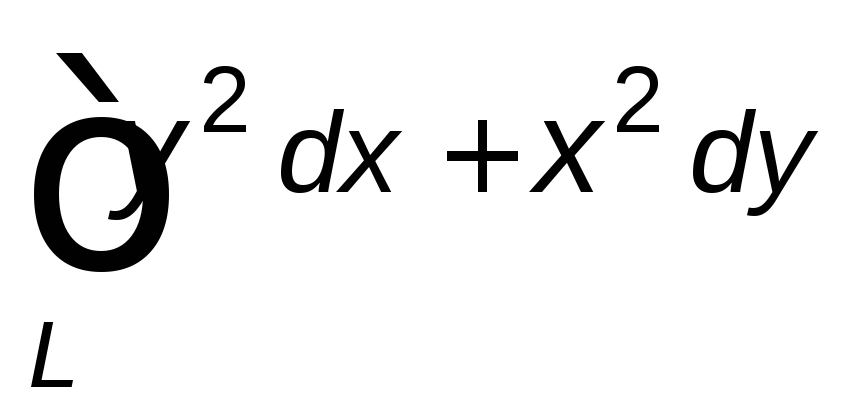 ,
,
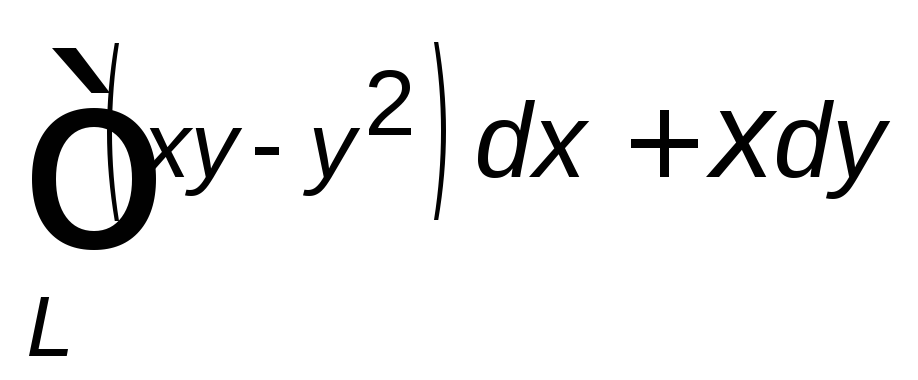 ,
,
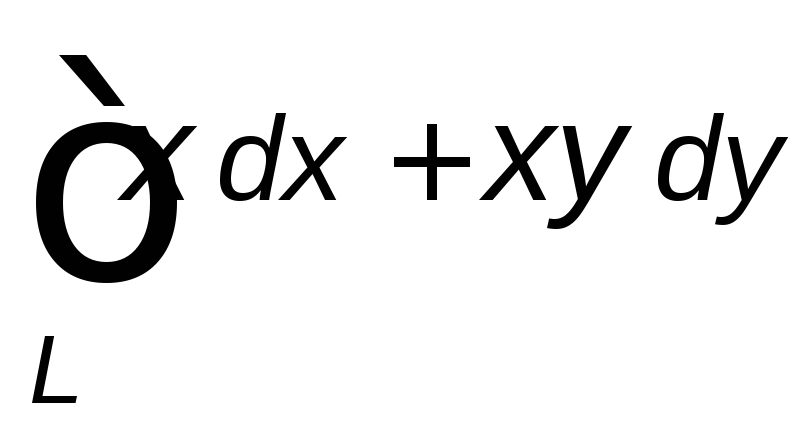 ,
,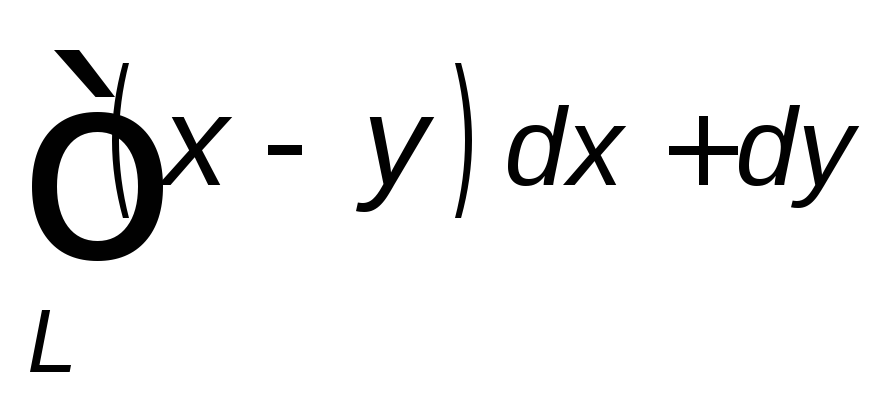 ,
, ,
,
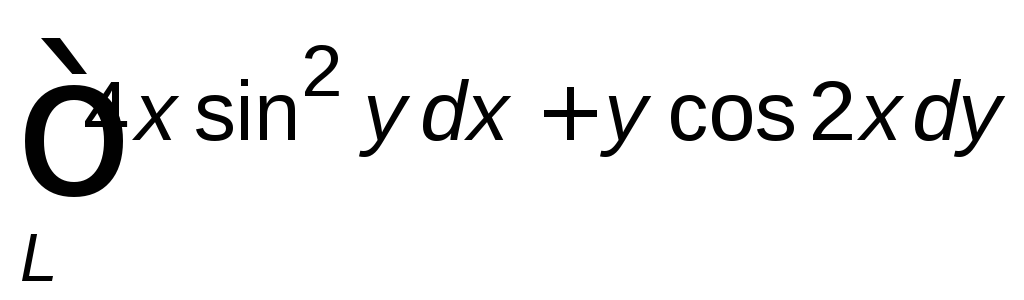 ,
,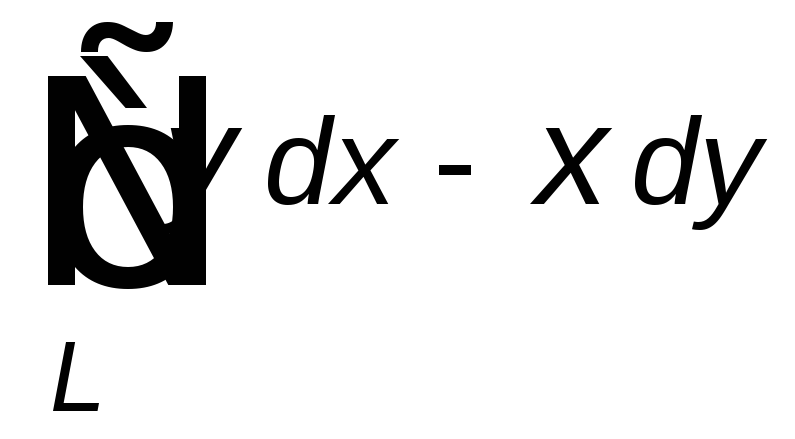 ,
,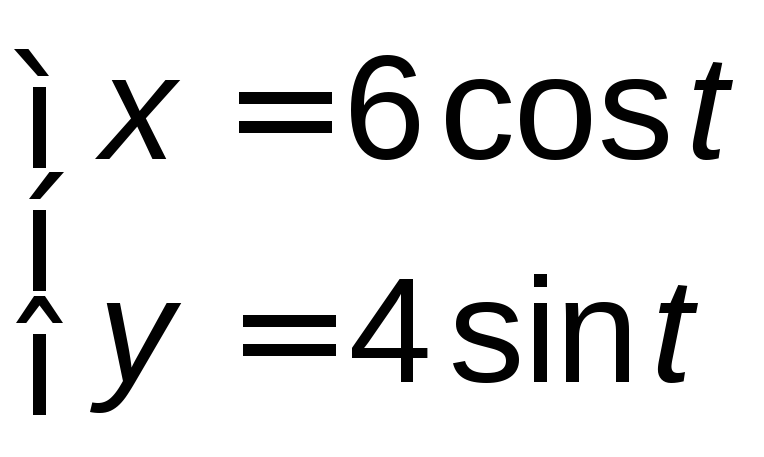 при положительном направлении обхода
контура.
при положительном направлении обхода
контура.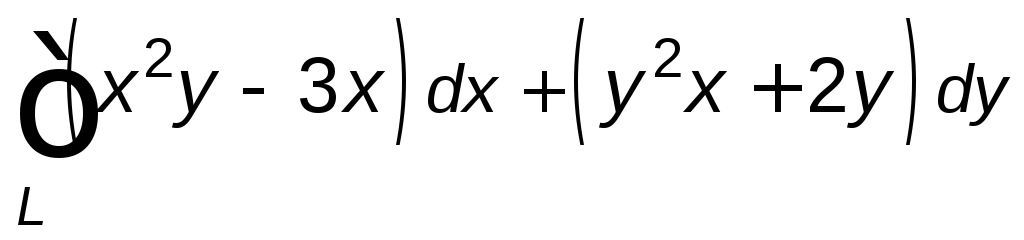 ,
,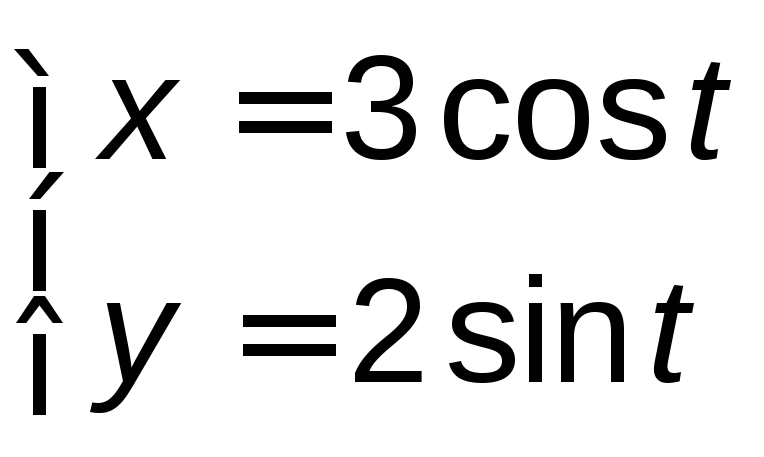 ,
,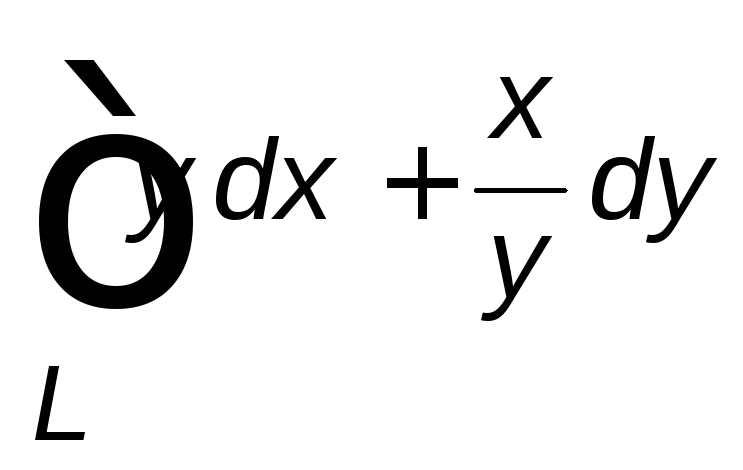 ,
,
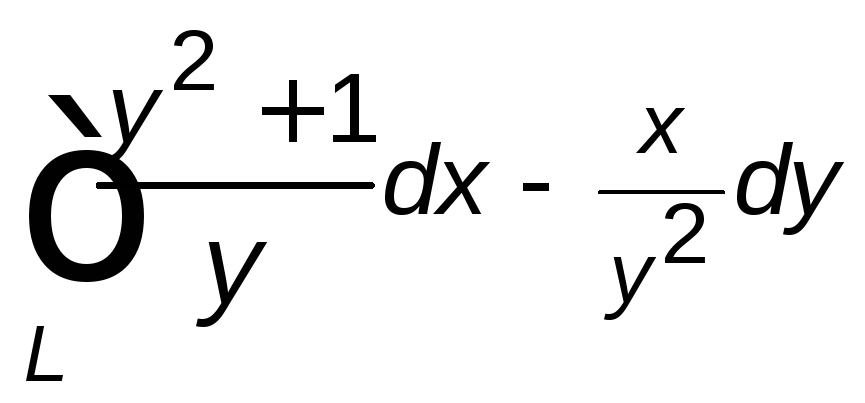 ,
,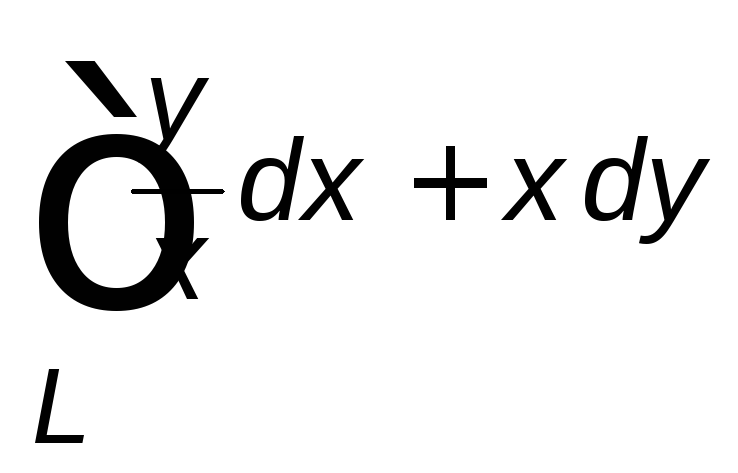 ,
,
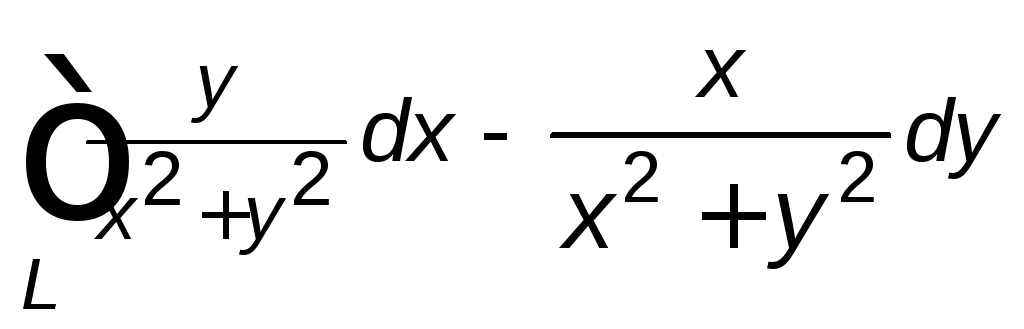 ,
,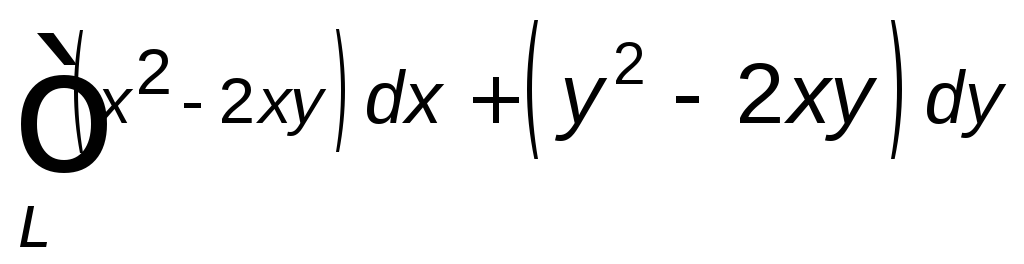 ,
,
 ,
,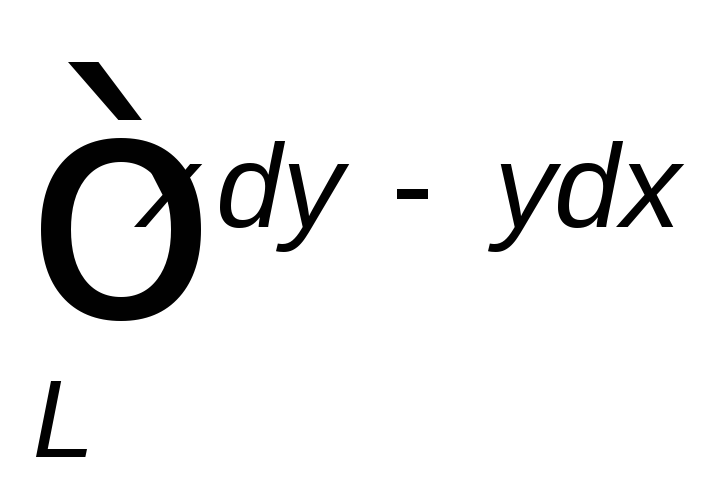 ,
,
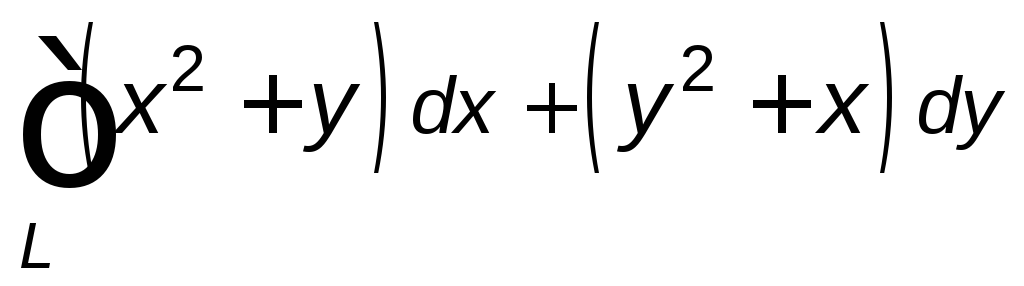 ,
, ,
от точки
,
от точки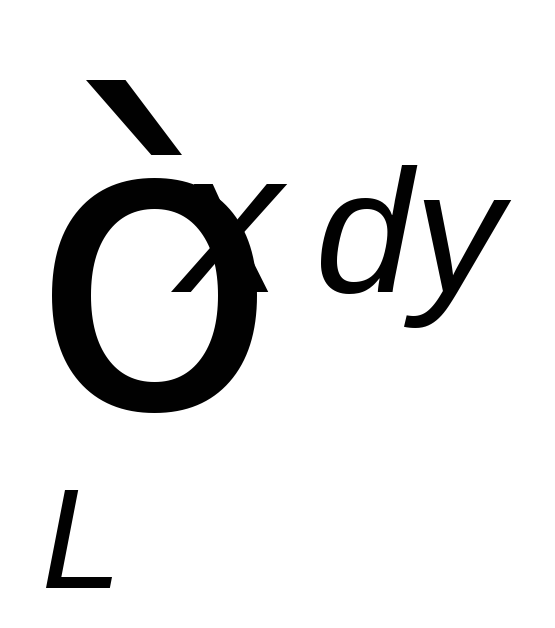 ,
,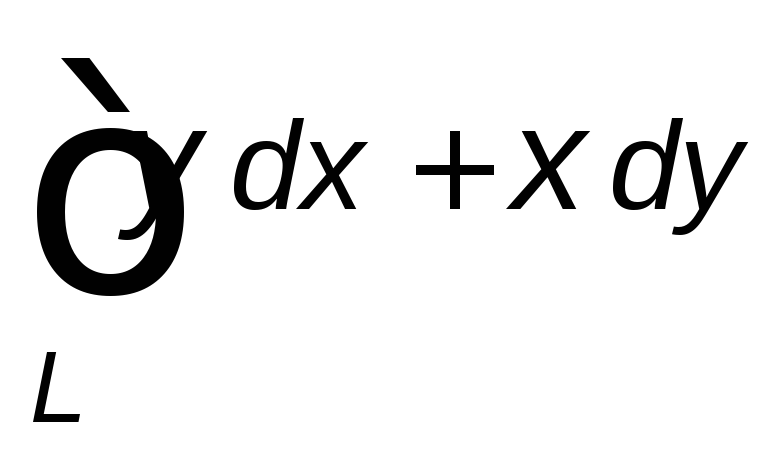 ,
где
,
где
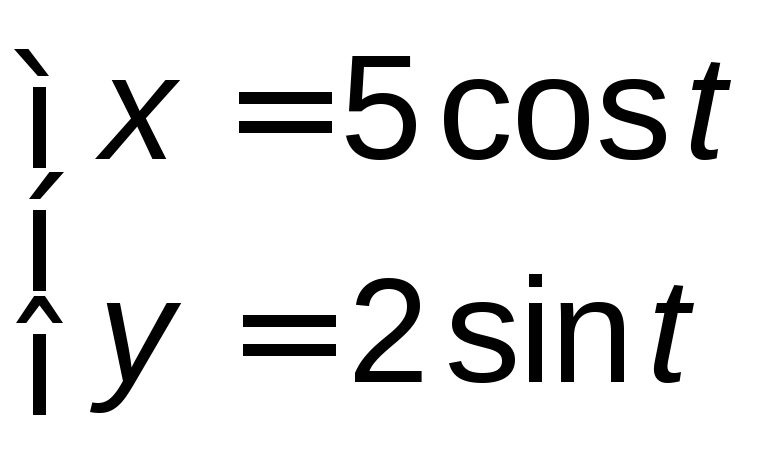 ,
«пробегаемая» по ходу часовой стрелки.
,
«пробегаемая» по ходу часовой стрелки.