
dln001
.pdfбольше ребер, совпадающих с ребрами TK: Повторяя описанную процедуру для TK è T 0 ; затем для TK è T 00
S S и т. д., получаем конечную последовательность кратчайших остовов, сходящуюся к TK:
Формализованная запись алгоритма. Введем следующие обозначения:
1; 2; : : : ; n числовые метки вершин графа; i счетчик ребер графа;
k счетчик ребер остова;
E список ребер графа, упорядоченных по длине. Каж-
дая строка списка состоит из пары ei;1 è ei;2; являющихся числовыми метками концов i -го ребра;
t номер фрагмента остова;
S список принадлежности вершин графа фрагментам
остова. Значение sj равно номеру фрагмента, которому на текущей итерации принадлежит вершина j: Первоначально все элементы списка равны нулю. По завершении работы алгоритма все элементы S равны единице. Для рассмотренного выше примера динамика изменения списка отражена в табл. 3.4. На итерациях 4; 7; 9; 12 14 состояние списка не меняет ся, так как соответствующие ребра не могут быть включены в остов.
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.4 |
Итерация |
s1 |
s2 |
s3 |
s4 |
s5 |
s6 |
s7 |
s8 |
s9 |
s10 |
остоваФрагменты |
(ребро) |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
T1:=f1; 5g |
2 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
T1:=T1 + f4; 5g |
3 |
1 |
2 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
T2:=f2; 3g |
5 |
1 |
2 |
2 |
1 |
1 |
0 |
0 |
0 |
3 |
3 |
T3:=f9; 10g |
6 |
1 |
2 |
2 |
1 |
1 |
0 |
0 |
1 |
3 |
3 |
T1:=T1 + f5; 8g |
8 |
1 |
2 |
2 |
1 |
1 |
3 |
0 |
1 |
3 |
3 |
T3:=T3 + f6; 10g |
10 |
1 |
2 |
2 |
1 |
1 |
3 |
2 |
1 |
1 |
1 |
T2:=T2 + f3; 7g |
11 |
1 |
2 |
2 |
1 |
1 |
1 |
2 |
1 |
1 |
1 |
T1:=T1 + T3; Tn3 |
15 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
T1:=T1 + T2; Tn2 |
61
С использованием введенных обозначений запись алгорит- |
||||||||||||||||||||||||||
ма принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
begin |
|
|
|
|
|
|
{ Ê Ð À Ñ Ê À Ë } |
|
|
|||||||||||||||||
i := 1; t := 1; k := 1; { Формировать первый фрагмент остова } |
||||||||||||||||||||||||||
se1;1 := t; se1;2 := t; |
|
|
|
{ на основе кратчайшего ребра графа } |
||||||||||||||||||||||
output(i); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ и напечатать номер ребра. } |
|||||||||
while (k<(n¡1)) & (i<m) do |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
:= i+1; |
|
|
|
|
|
|
|
|
|
{ Перейти к следующему ребру. } |
|||||||||||||||
8 ifi |
(sei;1 =0) & (sei;2 =0) |
|
|
|
{ Если ребро не имеет общих } |
|||||||||||||||||||||
> |
|
|
|
|
|
k := k+1; |
|
{ вершин ни с одним из фрагментов, } |
||||||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
{ включить ребро в остов, } |
||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
t := t+1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ создав } |
|||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
> |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> then |
|
|
:= t; |
|
|
|
|
:= t; |
|
|
|
|
|
{ новый фрагмент, } |
||||||||||||
> |
|
|
|
|
|
s |
|
|
s |
|
|
|
|
|
|
|
|
|
||||||||
> |
|
|
|
> |
ei;2 |
|
|
|
|
|
ei;1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
< output |
(i); |
|
|
|
|
|
|
|
{ и напечатать номер ребра. } |
|||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> else |
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ Если ребро имеет общую } |
||||||||||
> if |
(s |
: |
|
|
|
|
|
|
=0) |
|
|
|
|
|
||||||||||||
> |
|
|
=0) & (s |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
> |
|
|
ei;1 |
|
|
|
|
|
ei;2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
{ вершину с одним из фрагментов, то } |
||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
> |
|
|
|
|
|
k := k+1; |
|
|
|
|
|
|
|
|
{ включить ребро в остов, } |
|||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
ss |
|
:= se |
|
|
; |
|
|
{ присоединив его к фрагменту, } |
||||||||||||
> |
|
|
|
|
|
i;1 |
i;2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
> then |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
> |
|
|
|
( output |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
> |
|
|
|
(i); |
|
|
|
|
|
|
|
|
{ и напечатать номер ребра. } |
|||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> else |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> if |
(sei;1 =0) & (ssi;2 =0) |
|
|
|
|
|
{ Если ребро имеет общую } |
|||||||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
> |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
{ вершину с одним из фрагментов, то } |
||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
k := k+1; |
|
|
|
|
|
|
|
|
{ включить ребро в остов, } |
|||||||||||
|
|
|
|
|
sei;2 |
:= sei;1 ; |
|
|
{ присоединив его к фрагменту, } |
|||||||||||||||||
> then |
( output |
|
|
|
|
|
|
|
|
|
|
{ и напечатать номер ребра. } |
||||||||||||||
> |
|
|
|
(i); |
|
|
|
|
|
|
|
|
||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> else |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> if |
(s |
|
=0) & (s |
|
=0) & (s |
ei;1 |
=s |
|
) { Если концы ребра } |
|||||||||||||||||
> |
|
|
ei;1 |
|
|
|
|
|
ei;2 |
|
|
|
|
|
|
|
|
ei;2 |
|
|
|
|||||
> |
|
|
|
|
6 |
|
|
|
|
|
6 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
{ принадлежат разным фрагментам, } |
|||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
k := k+1; |
|
|
|
|
|
|
|
|
{ включить ребро в остов, } |
|||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
for |
j := 1 |
to |
n |
do |
|
|
|
|
{ объединив фрагменты } |
|||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
if |
|
sj=max(se |
|
|
; se |
|
|
) |
|
{ под меньшим } |
||||||||||
> |
|
|
|
|
|
|
|
|
|
i;1 |
i;2 |
|
|
|
||||||||||||
> then |
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
> |
|
|
then |
|
sj := min(sei;1 ; sei;2 ); |
{ номером, } |
||||||||||||||||
> |
|
|
|
> |
|
|
|
|
|
|
|
|
||||||||||||||
> |
|
|
|
< |
½ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
output |
(i); |
|
|
|
|
|
|
|
{ и напечатать номер ребра. } |
|||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
> else |
>{ Концы ребра принадлежат одному фрагменту } |
|||||||||||||||||||||||||
> |
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ Не включать ребро в остов. } |
||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
> |
|
|
|
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
if k>= (n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
¡ |
|
'Получено кратчайшее остовное дерево.' |
) |
||||||||||||||||||||
then output |
||||||||||||||||||||||||||
: |
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
else output ('Получен кратчайший остовный лес.' ) |
|
|||||||||||||||||||||||||
end. |
|
|
|
|
|
{ Ê Ð À Ñ Ê À Ë } |
|
|
||||||||||||||||||
62
Оценим трудоемкость приведенного варианта реализации алгоритма Краскала применительно к (n; m) -графу.
В худшем случае (самое длинное ребро принадлежит крат- чайшему остову) внешний цикл перебора ребер графа должен повториться m¡1 раз. Кроме того, в тех случаях, когда включение ребра приводит к объединению двух фрагментов будущего остова, должна быть выполнена процедура объединения множеств их вершин. Число повторений соответствующего цикла равно n: Учитывая все это, можно утверждать,
что трудоемкость алгоритма не хуже чем O(mn): Это весьма завышенная оценка, поскольку далеко не всегда ребро с максимальным весом входит в остов, и совсем не обязательно, что включение очередного ребра должно приводить к слиянию некоторой пары фрагментов.
В заключение отметим, что алгоритм предполагает упорядоченность списка ребер, а это, в свою очередь, требует выполнения еще порядка O(m log2 m) операций. При достаточ- но большом m именно эта составляющая процесса получения кратчайшего остова может оказаться основной в общем балансе трудоемкости.
3.4.2. Алгоритм Прима
Описание алгоритма. В отличие от алгоритма Краскала, алгоритм Прима обеспечивает построение остова графа G(V; E); заданного списком ребер, путем наращивания един-
ственного древовидного фрагмента T (V T; ET ); который вна- чале вообще не имеет ребер и состоит из одной произвольно выбранной вершины графа. На каждой итерации к фрагменту добавляется самое короткое ребро из числа ребер, у которых одна из концовых вершин vi уже включена в строя- щийся остов, а другая vj åùå íåò, ò. å. ETk:=ETk¡1+fvi; vjg è
V Tk:=V Tk¡1+vj; ãäå vi2V Tk¡1; vj62V Tk¡1; à ci;j минимально.
Процесс заканчивается после присоединения к T n¡1 ребер. Таким образом, при выполнении алгоритма формируется последовательность деревьев: T0; T1; : : : ; Tn¡1; ãäå T0=hfvg; ;i; à Tn¡1 кратчайший остов. Если список упорядочен по воз-
63
растанию весов ребер, то включению в остов на очередной итерации подлежит первое от начала списка ребро fvi; vjg; отвечающее указанному выше условию.
Построение остова для графа, изображенного на рис. 3.10, иллюстрирует табл. 3.5, аналогичная табл. 3.3.
|
|
|
|
|
|
|
|
|
Таблица 3.5 |
|||
e |
a |
b |
lab |
Ti |
|
|
|
|
V Ti |
i |
||
|
|
|
|
T0=hfv1g; ;i |
|
|
fv1g |
|
|
|
||
1 |
v1 |
v5 |
2 |
T1 := T0 + fv1; v5g |
fv1; v5g |
|
|
1 |
||||
2 |
v4 |
v5 |
3 |
T2 := T1 + fv4; v5g |
fv1; v4; v5g |
|
2 |
|||||
3 |
v2 |
v3 |
5 |
T8 := T7 + |
f |
v2 |
; v3 |
g |
fv1; v2; v3; v4; v5; |
8 |
||
|
|
|
|
|
|
|
v6; v8; v9; v10 |
g |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
v1 |
v4 |
7 |
|
|
|
|
|
|
|
|
|
5 |
v9 |
v10 |
8 |
T6 := T5 + fv9; v10g |
fv1; v4; v5; v6; v8; v9; v10g |
6 |
||||||
6 |
v5 |
v8 |
10 |
T3 := T2 + fv5; v8g |
fv1; v4; v5; v8g |
|
3 |
|||||
7 |
v4 |
v8 |
13 |
|
|
|
|
|
|
|
|
|
8 |
v6 |
v10 |
14 |
T5 := T4 + fv6; v10g |
fv1; v4; v5; v6; v8; v10g |
5 |
||||||
9 |
v6 |
v9 |
14 |
|
|
|
|
|
|
|
|
|
10 |
v3 |
v7 |
17 |
T9 := T8 + |
f |
v3 |
; v7 |
g |
fv1; v2; v3; v4; v5; |
9 |
||
|
|
|
|
|
|
|
v6; v7; v8; v9; v10 |
g |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
v5 |
v6 |
20 |
T4 := T3 + fv5; v6g |
fv1; v4; v5; v6; v8g |
4 |
||||||
12 |
v2 |
v7 |
22 |
|
|
|
|
|
|
|
|
|
13 |
v8 |
v9 |
23 |
|
|
|
|
|
|
|
|
|
14 |
v4 |
v9 |
23 |
|
|
|
|
|
|
|
|
|
15 |
v6 |
v3 |
25 |
T7 := T6 + fv3; v6g; |
fv1; v3; v4; v5; v6; v8; v10g |
7 |
||||||
: : : |
: : : |
: : : |
: : : |
: : : |
|
|
|
|
: : : |
|
|
|
Здесь содержимое столбца Ti показывает, как растет единственный древовидный фрагмент формируемого остова, столбец V Ti отражает рост множества вершин, принадлежащих этому фрагменту, а номер итерации, на которой ребро вклю- чается в остов, указан в столбце i .
Пусть начальный фрагмент состоит из вершины v1: Анализ первого ребра списка показывает, что оно отвечает условию включения в остов. Полученное дерево имеет две вершины v1 è v5: Проверяя второе ребро, убеждаемся, что его также следует включить в остов. Новый фрагмент содержит
64
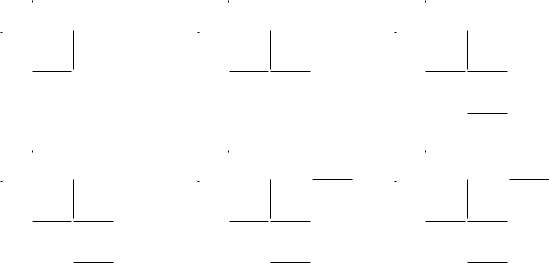
уже три вершины V T2=fv1; v4; v5g: Третье ребро пока пропускаем, так как ни v2 íè v3 не принадлежат V T2: То же самое можно сказать и о пятом ребре. Оба конца четвертого ребра, наоборот, принадлежат V T2; значит, его включение приведет к появлению цикла, что недопустимо. И только шестое ребро отвечает условию на включение. Таким образом, после третьей итерации получаем дерево T3; состоящее из трех ребер,
ò. å. ET3=ffv1; v5g; fv4; v5g; fv5; v8gg: На четвертой итерации к |
||||||||||||||||||||||||||||||
дереву добавляется одиннадцатое ребро, на пятой восьмое |
||||||||||||||||||||||||||||||
и т. д. Построение остова завершается на девятой итерации |
||||||||||||||||||||||||||||||
присоединением десятого ребра. |
На рис. 3.13 представлены |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
vr1 |
|
vr2 |
vr3 |
5 |
|
|
vr1 |
|
|
vr2 |
vr3 |
6 |
|
|
|
vr1 |
|
|
vr2 |
|
vr3 |
||
|
|
ÀT |
|
|
|
|
ÀT |
5 |
|
|
|
|
ÀT |
6 |
|
|
|
|
|
|
||||||||||
|
v4 |
r |
3 |
vr5 |
|
rv6 rv7 |
v4 |
r |
|
vr5 |
|
rv6 rv7 |
v4 |
r |
|
vr5 |
|
rv6 rv7 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
vr8 |
|
|
vr9 |
|
vr10 |
|
|
vr8 |
|
vr9 |
|
|
vr10 |
|
|
vr8 |
|
vr9 |
|
|
vr10 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
v |
|
v |
v |
|
|
|
v |
|
|
v |
v |
|
|
|
|
v |
|
|
v |
|
v |
|
|
|
7 |
|
|
|
|
|
r1 |
|
r2 r3 |
8 |
|
|
r1 |
|
|
r2 |
r3 |
9 |
|
|
|
r1 |
|
|
r2 |
|
r3 |
|
|
|
|
|
ÀT7 |
|
|
|
|
ÀT8 |
|
|
|
|
ÀT9 |
|
|
|
|
|
|
||||||||||||
|
v4 |
r |
|
|
|
vr5 |
|
rv6 |
rv7 |
v4 |
r |
|
vr5 |
|
|
rv6 |
rv7 |
v4 |
r |
|
vr5 |
|
|
rv6 |
|
rv7 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
vr8 |
|
|
vr9 |
|
vr10 |
|
|
vr8 |
|
vr9 |
|
|
vr10 |
|
|
vr8 |
|
vr9 |
|
|
vr10 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
S |
список принадлежности вершин графа формируе- |
||||||||||||||
|
|
мому фрагменту остова. Если к текущей итерации |
|
|||||||||||||
|
|
вершина |
j |
уже включена в остов, то sj=1; èíà- |
||||||||||||
|
|
÷å sj=:0 Первоначально все элементы списка равны |
||||||||||||||
|
|
нулю, кроме элемента, соответствующего начальной |
||||||||||||||
|
|
вершине. По завершении работы алгоритма все эле- |
||||||||||||||
|
|
менты S равны единице. Для рассмотренного вы- |
||||||||||||||
|
|
ше примера динамика изменения списка отражена |
||||||||||||||
|
|
â òàáë. 3.6. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.6 |
|
|
Итерация |
s1 |
s2 |
s3 |
s4 |
s5 |
s6 |
|
s7 |
s8 |
s9 |
s10 |
остоваФрагменты |
|
||
|
(ребро) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
T0=hfv1g; ;i |
|
|
|
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
T1:=T0 + f1; 5g |
|
|
|
2 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
0 |
T2:=T1 + f4; 5g |
|
|
|
3 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
T3:=T2 + f5; 8g |
|
|
|
4 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
T4:=T3 + f5; 6g |
|
|
|
5 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
T5:=T4 + f6; 9g |
|
|
|
6 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
T6:=T5 + f3; 6g |
|
|
|
7 |
|
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
T7:=T6 + f3; 2g |
|
|
|
8 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
T8:=T7 + f2; 3g |
|
|
|
9 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
T9:=T8 + f3; 7g |
|
С использованием введенных обозначений запись алгорит- |
||||||||||||||||
ма принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
|||||
begin |
|
|
|
{ Ï Ð È Ì } |
{ Инициализация списка S } |
|||||||||||
for k := 1 to n do sk := 0; |
|
|
|
|||||||||||||
s1 := 1; |
|
|
|
{ Начать построение остова с вершины v1 } |
||||||||||||
for k := 1 to n¡1 do |
|
|
|
{ Цикл формирования остова } |
||||||||||||
8 |
i := 1; |
sei;1 =sei;2 do |
i := i+1; { Поиск включаемого ребра. } |
|||||||||||||
while |
||||||||||||||||
|
{Ребро найдено, включить его в остов } |
|||||||||||||||
> sei;1 :=1; |
sei;2 :=1; |
|
|
|
|
|
{ и напечатать номер. } |
|||||||||
< output |
(i); |
|
|
|
|
|
|
|
|
|||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
end. |
{ Ï Ð È Ì } |
Оценивая, как и ранее, по максимуму трудоемкость этого варианта алгоритма Прима, убеждаемся, что ее порядок равен O(nm) без учета трудоемкости сортировки списка ребер.
66
Рассмотрим еще один вариант реализации алгоритма, основанный на технике пометок вершин, не требующий предварительной сортировки ребер и использующий матрицу весов C: Покажем эту технику на примере графа, изображенного на рис. 3.10. Матрица весов этого графа имеет вид:
|
v3 |
2 |
v1 v2 v3 v4 |
v5 |
v6 v7 v8 v9 v10 |
|
|||||||||
|
|
15 |
|
1 |
|
251 |
17 |
1 1 1 |
3 |
|
|||||
|
v1 |
|
1 34 1 7 |
2 |
38 1 1 1 1 |
|
|
||||||||
|
v2 |
6 |
34 |
|
5 |
|
30 |
|
22 |
|
|
|
7 |
|
|
|
v4 |
17 |
1 11 11 13 |
1 1 131 231 11 |
|
||||||||||
C = |
v |
|
6 |
|
221 |
1 |
1 |
1 |
|
1 |
|
1 1 |
7 |
: |
|
|
|
6 |
2 |
17 |
|
1 1 1 |
|
35 |
7 |
|
|||||
|
v5 |
6 |
30 |
|
3 |
|
20 |
|
10 |
|
|
7 |
|
||
|
|
7 |
6 |
1 |
|
|
131 101 1 1 1 231 |
|
7 |
|
|||||
|
v8 |
6 |
|
25 |
|
7 |
|
||||||||
|
v6 |
6 |
38 |
|
|
20 |
|
|
|
14 14 |
7 |
|
|||
|
v10 |
6 |
1 |
1 1 |
|
|
14 35 |
1 |
8 |
1 |
7 |
|
|||
|
|
|
6 |
1 |
1 |
1 1 |
|
7 |
|
||||||
|
v9 |
4 |
1 |
1 1 |
14 |
|
1 |
|
1 |
5 |
|
||||
|
6 |
1 |
1 1 |
23 |
1 |
1 |
23 |
1 |
8 |
7 |
|
||||
|
|
|
6 |
|
|
|
|
7 |
|
||||||
Процесс получения остова отображен в табл. 3.7. Столбцы таблицы содержат числовые пометки (временные и постоянные), присваиваемые вершинам при выполнении алгоритма.
|
|
|
|
|
|
|
|
|
Таблица 3.7 |
||
Итера- |
v1 |
v2 |
v3 |
v4 |
v5 |
v6 |
v7 |
v8 |
v9 |
v10 |
p |
öèè |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
34 |
1 |
7 |
2 |
38 |
1 |
1 |
1 |
1 |
v1 |
2 |
|
30 |
1 |
3 |
|
20 |
1 |
10 |
1 |
1 |
v5 |
3 |
|
30 |
1 |
|
|
20 |
1 |
10 |
23 |
1 |
v4 |
4 |
|
30 |
1 |
|
|
20 |
1 |
|
23 |
1 |
v8 |
5 |
|
30 |
25 |
|
|
|
1 |
|
14 |
14 |
v6 |
6 |
|
30 |
25 |
|
|
|
1 |
|
|
8 |
v9 |
7 |
|
30 |
25 |
|
|
|
35 |
|
|
|
v10 |
8 |
|
5 |
|
|
|
|
17 |
|
|
|
v3 |
9 |
|
|
|
|
|
|
17 |
|
|
|
v2 |
pred |
|
6v1 |
6v1 |
6v1 |
v1 |
6v1 |
6v1 |
6v1 |
6v1 |
6v1 |
|
|
6v5 |
v6 |
v5 |
|
v5 |
6v10 |
v5 |
6v4 |
6v6 |
|
|
|
|
v3 |
|
|
|
|
v3 |
|
v6 |
v9 |
|
Значение пометки любой вершины vi; еще не включенной в остов, равно длине ребра, связывающего vi с ближайшей вершиной, уже вошедшей в остов. На каждой итерации в остов
67
включается вершина с минимальной временной пометкой, которая в дальнейшем уже не меняется (в таблице выделена шрифтом). Сама вершина считается постоянно помеченной и фиксируется в столбце p таблицы. После этого производится пересчет временных пометок всех вершин, соседних с последней постоянно помеченной вершиной, по формуле:
l(vi) = min[l(vi); cp;i];
ãäå l(vi) пометка вершины vi; p последняя постоянно помеченная вершина. Если l(vi) меняет значение (уменьшается), следует скорректировать содержимое строки pred â
столбце vi; заменив прежнее значение на значение p:
Пусть T0 состоит из единственной вершины v1: Рассматривая на первой итерации v1 как последню постоянно поме- ченную, заносим ее в столбец p первой строки. Используя
матрицу C; присваиваем всем остальным вершинам времен-
ные пометки l(vi)=c1;i: Говорят, что вершины получили свои пометки из v1: Фиксируем это в последней строке таблицы строке "вершин-предшественниц", обозначенной как pred: Затем отыскиваем минимальную временную пометку. В
нашем примере это пометка вершины v5; равная 2. Далее счи- таем найденную пометку постоянной, а вершину v5 постоянно помеченной, записываем ее в столбец p и включаем в форми-
руемый остов ребро fv5; v1g: Отметим, что вес включаемого ребра равен значению найденной пометки.
На следующей итерации пересчитываем временные пометки по формуле l(vi)= min[l(vi); c5;i]: При этом, если значение
пометки l(vi) меняется (уменьшается), корректируем и значе- ние в последней строке столбца vi; заменяя его текущим зна- чением p=v5: Поскольку изменяются l(v2); l(v4); l(v6) è l(v8); следует скорректировать содержимое 2, 4, 6 и 8 столбцов последней строки, заменив его на v5: Вновь отыскиваем минимальную временную пометку. Теперь это l(v4)=3; которая становится постоянной. Соответственно последней постоянно помеченной вершиной p становится v4; а в остов включается ребро
68
На третьей итерации после пересчета временных пометок, причем изменяется только пометка l(v9); минимальной оказывается пометка вершины v8; и в остов включается ребро fv8; v5g: Вторая вершина реберной пары берется из последней строки восьмого столбца.
На четвертой итерации (значения всех пометок сохраняются) минимальной оказывается пометка l(v6)=20; на пятой (изменяются l(v3) è l(v9) ) минимальна l(v9)=14 и т. д. Процесс завершается на девятой итерации после того, как все вершины получают постоянные пометки (см. табл. 3.6).
В итоге получаем список ребер, образующих кратчайший
остов: fv2; v3g; fv3; v6g; fv4; v5g; fv5; v1g;fv6; v5g;fv7; v3g;fv8; v5g;
fv9; v6g;fv10; v9g: Первая вершина пары берется из заголовка столбца, а вторая из последней строки того же столбца. Результат полностью соответствует остову на рис. 3.13(9). Длина найденного остова равна сумме всех постоянных пометок, которые, как легко проверить, равны весам ребер, вошедших в остов.
Строка вершин-предшественниц pred может быть сформирована и после того, как все вершины получат постоянные пометки. Для этого достаточно в каждом столбце таблицы найти самую верхнюю строчку с минимальной пометкой. Зна- чение predi содержится в столбце p этой строки.
В заключение отметим, что трудоемкость рассмотренного варианта реализации алгоритма Прима имеет порядок O(n2):
Действительно, число итераций внешнего цикла равно n¡1 причем на каждой итерации следует обработать строку матрицы C:
69
4. Пути и маршруты в графах
Существует большое разнообразие задач, связанных с путями и маршрутами в графе, начиная от стандартных задач на существование, пересчет и перечисление и кончая задача- ми поиска путей, отвечающих определенным требованиям. Такими требованиями могут быть: требования максимальности (минимальности) длины, пропускной способности или надежности пути; требования к множеству вершин (ребер), принадлежащих (не принадлежащих) пути, и т. п. При этом сами графы могут иметь различные свойства, например, быть или не быть ориентированными, циклическими, взвешенными и т. д. Наконец, один и тот же граф может быть описан по-разному. Поэтому даже одна и та же задача для различных по своим характеристикам и способу описания графов может решаться по-разному.
4.1. Существование путей
Эта задача эквивалентна задаче на достижимость в орграфе, решение которой рассмотрено в разд. 2. Действительно, матрица достижимости полностью определяет наличие или отсутствие пути для любой упорядоченной пары вершин. Поэтому ограничимся примером.
На рис. 4.1 изображены граф G и его матрица достижимости R , полученная одним из ранее рссмотренных способов.
|
|
|
d |
|
|
|
|
a b c d e |
|
||||
G |
@I |
@ |
|
|
R = c 2 |
3: |
|||||||
|
|
1 |
1 |
1 |
1 |
1 |
|||||||
|
|
6 |
|
|
a |
|
1 |
1 |
1 |
1 |
1 |
|
|
|
a |
r |
@ |
c |
|
|
|||||||
|
|
b |
b |
|
1 |
1 |
1 |
1 |
1 |
|
|||
|
- @R |
|
|
|
|||||||||
|
r |
@ |
r |
r |
d |
6 |
1 |
1 |
1 |
1 |
1 |
7 |
|
|
|
|
@? |
|
|||||||||
|
|
|
e |
|
|
e |
6 |
1 |
1 |
1 |
1 |
1 |
7 |
|
|
|
r |
|
|
|
4 |
|
|
|
|
|
5 |
Ðèñ. 4.1
Простая проверка убеждает, что для любой пары вершин в графе имеется хотя бы один путь. Именно это и следует из приведенной матрицы, поскольку все ее элементы равны 1.
70
