
§1.Постановка задачи
В
классе скалярных кусочно-непрерывных
управляющих воздействий u(t),
определенных на заданном временном
промежутке T= ,
рассмотрим следующую квазилинейную
задачу терминального управления:
,
рассмотрим следующую квазилинейную
задачу терминального управления:
J(u)= x(t*)→max,
x(t*)→max,
 ,
x(
,
x( )=
)= ,
(1.1)
,
(1.1)
 ,
Hx(t*)+µh(x(t*))=g,
,
Hx(t*)+µh(x(t*))=g,
где
µ-малый положительный параметр,
x-n-вектор,g-m
вектор (m<n).
Остальные элементы задачи имеют
соответствующее размеры, при этом A(t),
b(t),

Предполагается также, что rank H=m.
Результаты,
которые будут получены в дальнейшем,
справедливы и для отрицательных значений
µ, если только они достаточно малы по
модулю. Поэтому будем считать областью
изменения малого параметра некоторую
окрестность нуля
 .
.
При некоторых достаточно общих предположениях оптимальное управление в задаче является релейным и сохраняет при этом структуру решения базовой задачи
 ,
x(
,
x( )=
)= ,
,
 ,
(1.2)
,
(1.2)
Hx(t*)=g,
J(u)= x(t*)→max,
x(t*)→max,
которая
формально получается из исходной при
µ=0. Далее будет разработан и обоснован
алгоритм, позволяющий для заданного
натурального числа s, ,
построить релейное асимптотически
субоптимальное управление s-го
порядка в рассмотренной задаче. Точки
переключения этого асимптотического
приближения представляют собой полиномы
Тейлора s-ой
степени точек переключения оптимального
управления, которые являются функциями
малого параметра, причем функциями из
класса Сp.
Кроме того, будет показано, как можно
использовать построенные асимптотические
приближения для точного решения задачи
(1.1) при данном значении малого параметра.
,
построить релейное асимптотически
субоптимальное управление s-го
порядка в рассмотренной задаче. Точки
переключения этого асимптотического
приближения представляют собой полиномы
Тейлора s-ой
степени точек переключения оптимального
управления, которые являются функциями
малого параметра, причем функциями из
класса Сp.
Кроме того, будет показано, как можно
использовать построенные асимптотические
приближения для точного решения задачи
(1.1) при данном значении малого параметра.
§2. Базовая задача
Первый этап алгоритма асимптотического решения задачи (1.1) состоит в нахождении оптимального управления в задаче (1.2). Причем заметим, что это задача в отличие от исходной является линейной.
Предположение
1.1.
В задаче (1.2) существует оптимальное
управление u0(t),
t ,
которое является нормальным.
,
которое является нормальным.
При
этом предположении сопряженная переменная
 0(t),
0(t), соответствущая
в силу принципа максимума оптимальному
управлению, является решение начальной
задачи
соответствущая
в силу принципа максимума оптимальному
управлению, является решение начальной
задачи
 =
=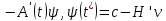 0,
0,
где
 0
–m-вектор
множителей Лагранжа. Согласно принципу
максимума
0
–m-вектор
множителей Лагранжа. Согласно принципу
максимума
 ,
t
,
t Заметим,
что коуправление представило также в
виде
Заметим,
что коуправление представило также в
виде
 t
t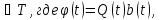
 ,
а
,
а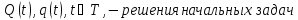

Оптимальную
траекторию, порожденную управление
 через
через
 .
.
Предположение
1.2.
Коуправление
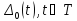 ,
имеет конечное число нулей
,
имеет конечное число нулей
 01,…,t0t,
занумерованных в порядке возрастания,
при этом выполнены условия
01,…,t0t,
занумерованных в порядке возрастания,
при этом выполнены условия
 0(t0j)
0(t0j) rank(
rank( t0j),
t0j),
 =m.
=m.
Тогда,
как следует из (1.3), оптимальное управление
является релейным:
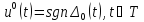 ,
а моменты
,
а моменты
 01,…,t0l
и только они будут его точками
переключения. Заметим также, что при
сделанном предположении
01,…,t0l
и только они будут его точками
переключения. Заметим также, что при
сделанном предположении
 .
.
После
решения базовой задачи введем в
рассмотрение числа
 0,
0, 1,…,
1,…, l:
l: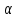 0=
0= k=(-1)k
k=(-1)k 0,
0, .
.
§3.Основная теорема
Прежде чем продолжить изложение алгоритма построения асимптотически субоптимальных управлений в задаче (1.1), докажем теорему, которая устанавливает структуру и асимптотические свойства решения этой задачи. Доказательство будет конструктивным, и поэтому предопределит дальнейшие вычисления. Оно основано на следующих соображениях.
Правдоподобной выглядит гипотеза о том, что при сделанных предположениях оптимальное управление в задаче (1.1) с достаточно малым по модулю µ является релейным и сохраняет структуру решения базовой задачи, т.е. имеет вид
 1(µ),…,
1(µ),…, l(µ)),
l(µ)),
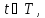 (1.4)
(1.4)
где
 1,…,
1,…, l
)=
l
)= (1.5)
(1.5)

Для
того, чтобы доступное управление вида
(1.4) было оптимальным в задаче (1.1), прежде
всего необходимо, чтобы оно было
допустимым. Это будет иметь место тогда
и только тогда, когда моменты tj(µ),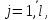 удовлетворяют системе уравнений
удовлетворяют системе уравнений
Hx (1.6)
(1.6)
где
x ,
, ,-траектория
квазилинейной системы, порожденная
управлением (1.5).
,-траектория
квазилинейной системы, порожденная
управлением (1.5).
Далее,
для оптимальности управления (1.4)
необходимо, чтобы оно удовлетворяло
принципу максимума, что будет иметь
место только тогда , когда точки
переключения tj(µ), являются
нулями коуправления. Таким образом,
если допустить, что оптимальное управление
является нормальным, и
являются
нулями коуправления. Таким образом,
если допустить, что оптимальное управление
является нормальным, и
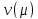 –соответствующий ему m-вектор
множителей Лагранжа, то этот вектор
вместе с моментом tj(µ),
–соответствующий ему m-вектор
множителей Лагранжа, то этот вектор
вместе с моментом tj(µ), должен
удовлетворять системе уравнений
должен
удовлетворять системе уравнений
 ,
, (1.7)
(1.7)
где
 ,
,
 *)=c-
*)=c- .
(1.8)
.
(1.8)
Приведенные соображения лежат в основе доказательства теоремы, на которую опирается алгоритм асимптотического решения задачи (1.1).
Теорема.
При выполнении предложений 1.1, 1.2 в задаче
(1.1) с достаточно малым (по модулю) µ
существует единственное оптимальное
управление u0(t,µ), нормальным.Точки переключения tj(µ),
нормальным.Точки переключения tj(µ), этого
управления и соответствующий ему в силу
принципа максимума m-вектора
множителей Лагранжа
этого
управления и соответствующий ему в силу
принципа максимума m-вектора
множителей Лагранжа
 удовлетворяют системе уравнений (1.6),
(1.7), причем tj(µ)
удовлетворяют системе уравнений (1.6),
(1.7), причем tj(µ) ,
tj(0)=t0j,
,
tj(0)=t0j, ,
,
 .
.
Доказательство. Прежде всего, убедимся, что система уравнений (1.6), (1.7) имеет решение. Для этого воспользуемся теоремой о неявной функции.
Введем
в рассмотрении векторы y=( y0=(
y0=( что
позволяет записать систему (1.6), (1.7) в
виде
что
позволяет записать систему (1.6), (1.7) в
виде
R(y,µ)=0, (1.9)
где
R(y,µ)=
Вектор-функция
R(y,µ)
определена в области

где

 -некоторые
достаточно малые положительные числа.
При сделанных предположениях о гладкости
функции, формирующих задачу (1.1), R(y,µ)
принадлежит классу
-некоторые
достаточно малые положительные числа.
При сделанных предположениях о гладкости
функции, формирующих задачу (1.1), R(y,µ)
принадлежит классу
 .
В этом можно убедиться с помощью теоремы
о дифференцируемости решений обыкновенных
дифференциальных уравнений по начальных
данных и параметрам, последовательно
применяя ее на промежутках постоянства
управления (1.5) к прямой и сопряженной
(1.8) системы.
.
В этом можно убедиться с помощью теоремы
о дифференцируемости решений обыкновенных
дифференциальных уравнений по начальных
данных и параметрам, последовательно
применяя ее на промежутках постоянства
управления (1.5) к прямой и сопряженной
(1.8) системы.
Заметим, что
u(t,t01,…,t0l)=u0(t), x(t,t01,…,t0l,0)=x0(t),
 .
.
Тогда


Это означает, что R(y0,0)=0.
Матрица Якоби системы (1.9), при вычислении которой удобно пользоваться формулой Коши, имеет вид
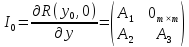 ,
(1.10)
,
(1.10)
где

 )-(
m
)-(
m матрица,
матрица,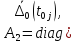
 )
-диагональная матрица l-го
порядка,
)
-диагональная матрица l-го
порядка, -( l
-( l матрица.
В силу предположения 1.2 матрица (1.10)
будет невырожденной.
матрица.
В силу предположения 1.2 матрица (1.10)
будет невырожденной.
Итак,
для системы (1.9) или, что то же самое,
(1.6), (1.7) выполнены все условия теоремы
о неявной функции. Согласно этой теоремы,
в некоторой окрестности нуля
 однозначно определены функции
однозначно определены функции
 ,
, ,
,
 ,удовлетворяющее
(1.6) ,(1.7) и условиям , tj(0)=t0j,
,удовлетворяющее
(1.6) ,(1.7) и условиям , tj(0)=t0j,
 .
Другими словами, при достаточно малом
µ в задаче (1.1) существуют допустимое
управление
.
Другими словами, при достаточно малом
µ в задаче (1.1) существуют допустимое
управление
 вида
(1.4) и вектор Лагранжа
вида
(1.4) и вектор Лагранжа
 (
( (t,
(t, )
являются нулями функции
)
являются нулями функции
 (t,
(t, )=
)= (t,
(t, )b(t),
)b(t),
 построенной по решению
построенной по решению
 (t,
(t, ),
),
 ,
сопряженной системы
,
сопряженной системы
 =
=
 )=c
)=c (
( ),
),
где (t,
(t, T,
T, траектория
прямой системы, порожденная управлением
траектория
прямой системы, порожденная управлением
 (t,
(t, t
t T.
T.
Опираясь
на предположение 1.2, с помощью теоремы
о неявной функции (используется
утверждение об однозначной разрешимости
уравнений) нетрудно доказать, что при
достаточно малом
 функция
функция
 (t,
(t, ,
t
,
t T,
обращается в нуль только в точках
переключения управления (1.4), при этом
T,
обращается в нуль только в точках
переключения управления (1.4), при этом
 (t,
(t, (t,
(t, T,
что эквивалентно
T,
что эквивалентно
 (t,
(t, )b(t)
)b(t) (t,
(t, (t,
(t, )b(t)u,
t
)b(t)u,
t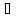 T.
(8.11)
T.
(8.11)
Таким
образом, управление (1.4) является
нормальной экстремалью Понтрягина с
m-вектором
множителей Лагранжа
 (
(
Покажем,
что экстремаль
 (t,
(t,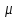 ),
t
),
t T,
будет оптимальным управлением, если
T,
будет оптимальным управлением, если
 мало. Предположим противное, тогда
существует такая последовательность
мало. Предположим противное, тогда
существует такая последовательность
 0,
что управление
0,
что управление
 (t,
(t, t
t T,
k=1,2,…,
не является оптимальным в задаче(1.1) с
T,
k=1,2,…,
не является оптимальным в задаче(1.1) с
 .
С помощью леммы Гронуолла нетрудно
доказать, что при достаточно малом
.
С помощью леммы Гронуолла нетрудно
доказать, что при достаточно малом
 допустимые траектории прямой динамической
системы в задаче (1.1) равномерно
ограничены. Кроме того, эта система
линейна по управлению, а множество
значений управляющих воздействий
представляет собой отрезок [-1,1], т.е.
выпуклый компакт. Тогда , если в задаче
(1.1) существует допустимое управление,
то существует и оптимальное (в классе
измеримых функций). Решение задачи
(1.1) с
допустимые траектории прямой динамической
системы в задаче (1.1) равномерно
ограничены. Кроме того, эта система
линейна по управлению, а множество
значений управляющих воздействий
представляет собой отрезок [-1,1], т.е.
выпуклый компакт. Тогда , если в задаче
(1.1) существует допустимое управление,
то существует и оптимальное (в классе
измеримых функций). Решение задачи
(1.1) с
 =
= k
обозначим через
k
обозначим через
 (t,
(t,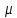 k),
t
k),
t
 ,
и пусть
,
и пусть
 (t,
(t,
 k),
t
k),
t T,
- соответствующая оптимальная траектория.
По предположению
T,
- соответствующая оптимальная траектория.
По предположению
 Jk=
J(
Jk=
J( (
( ,
,
 k
))- J(
k
))- J( (
( ,
,
 k))
> 0, k = 1,2, … .
(1.12)
k))
> 0, k = 1,2, … .
(1.12)
Это приращение критерия качества модно представить в виде
 (t,
(t,
 k)b(t)
k)b(t) k)
dt +O(
k)
dt +O(
 k)+
k)+
 k
k
 (
( )dt,k=1,2,
…, ( 1.13)
)dt,k=1,2,
…, ( 1.13)
где
 u
(t,
u
(t,
 k)=
k)= (t,
(t,
 k)-
k)-
 (t,
(t,
 k),
k),
 x(t,
x(t,
 k)
=
k)
=
 (t,
(t,
 k)
-
k)
-
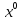 (t,
(t,
 k),
t
k),
t
 .
.
В силу(1.11) первый интеграл в правой части равенства (1.13) при достаточно больших k неположителен. Отсюда и из (1.12) следует

 )b(t)
)b(t) (
(
 )dt=
0,
)dt=
0,
что,
в свою очередь, влечёт за собой сходимость
последовательности функций
 )b(t)
)b(t)
 ,
t
,
t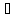 T,
по мере к нулю. В дальнейшем сводимость
по мере будем обозначать символом
T,
по мере к нулю. В дальнейшем сводимость
по мере будем обозначать символом ⇒.
Поскольку
⇒.
Поскольку
 )
=
)
= (
( )b(t),
t
)b(t),
t T
, равномерно сходится к коуправлению
T
, равномерно сходится к коуправлению
 (t),
(t),
 ,
базовой задачи, которое обращается в
нуль лишь в конечном числе точек, то
,
базовой задачи, которое обращается в
нуль лишь в конечном числе точек, то

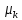 )
) .
Отсюда и из того, что
.
Отсюда и из того, что (
(
 )
) (t),
следует u(
(t),
следует u(
 )
)
 (t).По
теореме Рисса из любой последовательности
измеримых функций, сходящейся по мере,
можно выбрать подпоследовательность,
сходящуюся почти всюду. Чтобы не
усложнять обозначений, будем считать,
что сама последовательность
(t).По
теореме Рисса из любой последовательности
измеримых функций, сходящейся по мере,
можно выбрать подпоследовательность,
сходящуюся почти всюду. Чтобы не
усложнять обозначений, будем считать,
что сама последовательность
 (
(
 ),
),
 ,сходится
почти всюду к
,сходится
почти всюду к
 (t),
t
(t),
t T.Тогда
T.Тогда
 (
(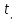
 )
→
)
→
 (t)
равномерно на T.
(t)
равномерно на T.
Поскольку
управление
 (
(
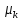 ),
t
),
t T,
k
= 1,2, … , является оптимальным, то для
него выполняется принцип максимума,
т.е. существует такой нулевой вектор
Лангранжа
T,
k
= 1,2, … , является оптимальным, то для
него выполняется принцип максимума,
т.е. существует такой нулевой вектор
Лангранжа
 (
(

 что почти всюду на T
что почти всюду на T
 (t,
(t, )b(t)
)b(t) (t,
(t,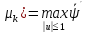 (t,
(t, )b(t)u,
k = 1,2, … , (1.14)
)b(t)u,
k = 1,2, … , (1.14)
где
 (t,
(t, ),
t
),
t T,-решение
сопряженной системы
T,-решение
сопряженной системы
 =
=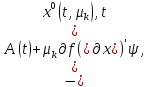
 )=
)= c
c
 (
(
Так
как векторы Лагранжа определяются с
точностью до положительного множителя,
то без ограничения общности можно
считать, что
 =
=
 ,
k
= 1,2, …, где
,
k
= 1,2, …, где
 = (1,
= (1,
 ).
В этом случае из последовательности
векторов
).
В этом случае из последовательности
векторов
 (
(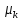 )
можно выбрать сходящуюся последовательность.
Чтобы не усложнять обозначений, будем
считать, что сама последовательность
является сходящейся. Обозначим её предел
через
)
можно выбрать сходящуюся последовательность.
Чтобы не усложнять обозначений, будем
считать, что сама последовательность
является сходящейся. Обозначим её предел
через
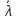 = (
= ( ,
,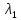 ,…,
,…, ).
).
Понятно,
что
 =
=
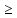 0. Тогда последовательность функций
0. Тогда последовательность функций
 (t,
(t,
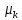 ),
t
),
t T,
будет равномерно сходиться к решению
T,
будет равномерно сходиться к решению
 (t),
t
(t),
t T,
начальной задачи
T,
начальной задачи
 =
=
 (t)
(t) ,
,
 (
( )
=
)
=
 c
c
 ,
,
 =
(
=
( …,
…, ).
).
Переходя
к пределу в (1.14) при
 всюду
на T
всюду
на T
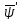 (t)b(t)
(t)b(t) (t)
=
(t)
=
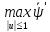 (t)b(t)u. (1.15)
(t)b(t)u. (1.15)
Поскольку
моменты
 являются точками переключения управления
являются точками переключения управления
 (t),
t
(t),
t
 ,
то из (1.15) следует
,
то из (1.15) следует
 (
(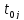 )b(
)b( )
=
)
=
 (
( )
-
)
-
 (
( )
= 0, j =
)
= 0, j =
 .
.
Так как наряду с этим
 (
( =
=
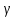 (
( )
-
)
-
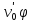 (
( ),
j
=
),
j
=
 ,
,
то
при предположении 1.2 векторы
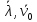 будут коллинеарны. Отсюда с учётом
равенства норм этих векторов получаем
будут коллинеарны. Отсюда с учётом
равенства норм этих векторов получаем
 ,
и соответственно
,
и соответственно
 ,
, .
Итак,
.
Итак,
 (t,
(t,
 )
) ,
,
 (t,
(t,
 )b(t)
)b(t) равномерно на Т. Используя этот факт,
соотношения (1.14) и предположение 1.2,
нетрудно доказать, что при достаточно
большом k
управление
равномерно на Т. Используя этот факт,
соотношения (1.14) и предположение 1.2,
нетрудно доказать, что при достаточно
большом k
управление
 ,
,
 , почти всюду имеет вид (1.5), где
, почти всюду имеет вид (1.5), где
 )
, где
)
, где
 )
)
 , тогда в силу однозначной разрешимости
системы (1.9) в окрестности точки (
, тогда в силу однозначной разрешимости
системы (1.9) в окрестности точки (
 )
)
управление
 ,
,
 , почти всюду совпадает с
, почти всюду совпадает с
 ,
,
 если к
достаточно велико, и как следствие
J(
если к
достаточно велико, и как следствие
J(
 . Полученное противоречие доказывает
оптимальность
. Полученное противоречие доказывает
оптимальность
 ,
,
 для достаточно малых
для достаточно малых
 .
.
Единственность оптимального управления доказывается аналогично, только неравенство (1.12) заменяется на равенство.
