17

Белорусский государственный университет

Физический факультет

Методические указания

к лабораторной работе

«Теплопроводность газов»

Утверждены на заседании

кафедры общей физики

« » 2002г.

Протокол № .

Минск 2002

Автор-составитель:

Солодухин И.А. – доцент

Задание: Экспериментально исследовать явление теплопроводности газов.

Оборудование и принадлежности: Установка для исследования явления теплопроводности газов.

Описание экспериментальной установки

Для исследования явления теплопроводности газов в работе выбран метод, позволяющий рассмотреть одномерный случай распространения тепла в газах. Для этого используется установка (рис.1), основным рабочим элементом которой является плоский нагреватель (рис.2).

Рис.1. Внешний вид установки для исследования теплопроводности газов.

Нагреватель 1 в установке представляет собой металлическую пластину, вмонтированную в корпус из теплоизолирующего материала. Нижняя холодная пластина 2 приведена в тепловой контакт с массивной дюралевой плитой 3, что обеспечивает хороший теплообмен с окружающей средой и позволяет поддерживать пластину 2 практически при постоянной комнатной температуре.

Пространство между пластинами для уменьшения теплообмена между исследуемым воздухом и окружающей средой изолировано боковыми стенками из пенопласта 4.

Для измерения температуры используются три термопары 5: одна вмонтирована в верхнюю пластину (нагреватель), другая – в нижнюю, а третья закреплена на конце тонкого вертикального стержня, расположенного между верхней и°нижней пластинами. Последняя термопара служит для измерения температуры воздуха и может перемещаться вверх и вниз. Каждая термопара подключена к датчику температуры.

На передней панели установки расположены: тумблер включения-выключения аппарата “сеть“, тумблер включения нагрева верхней пластины “нагрев“, тумблер переключения автоматического (“АВТ“) и ручного (“РУЧН“) режимов работы нагревателя, регулятор высоты средней термопары “высота“ и соответствующий ему индикатор, регулятор силы тока, протекающего через нагреватель, “ток нагрева“ и

Рис.2. Структурная схема установки для исследования теплопроводности газов

соответствующий ему индикатор, блок регистрации температур 6. В блок 6 входят индикатор значений температур 7, индикатор номеров каналов регистрации температур 8, кнопка 9 для автоматического переключения каналов, кнопка 10 для р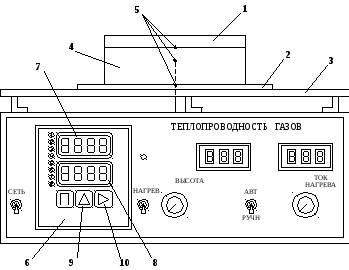учного переключения каналов. В данной установке рабочими являются третий, четвертый и пятый каналы: на пятом канале регистрируется температура нагревателя, на четвертом – температура воздуха между пластинами, на третьем – температура нижней (холодной) пластины.

Общее уравнение переноса

При нарушениях равновесия в средах возникают потоки тепла, либо массы, либо импульса и т.п. В связи с этим, соответствующие процессы носят название явлений переноса. Явления переноса представляют собой необратимые процессы.

Введем некоторую скалярную величину , которая характеризует некоторое молекулярное свойство, отнесенное к одной молекуле. Этим свойством может быть энергия, импульс, концентрация, электрический заряд и т.д.

Известно, что градиентом какой-либо величины (скалярной) , зависящей от координат, называется вектор, характеризующий быстроту изменения этой величины в пространстве. Этот вектор направлен в сторону наиболее быстрого возрастания и численно равен быстроте этого возрастания.

Если в равновесном состоянии величина постоянна по объему, то при наличии градиента , имеет место движение этой величины в направлении его уменьшения.

Для удобства расчетов предположим, что в неограниченной среде перенос количества происходит в одном направлении, вдоль которого направим ось . То есть, пусть ось направлена вдоль градиента . Выделим в среде площадку , перпендикулярную к оси (рис.1).

Рис.3. К выводу общего уравнения переноса

Площадку пересекают молекулы, пришедшие со всевозможных направлений и пересекающие ее в направлении отрицательных значений оси . Число молекул в объеме равно , где – концентрация молекул вещества. Частица движется со средней скоростью и, следовательно, проходит среднюю длину свободного пробега за время 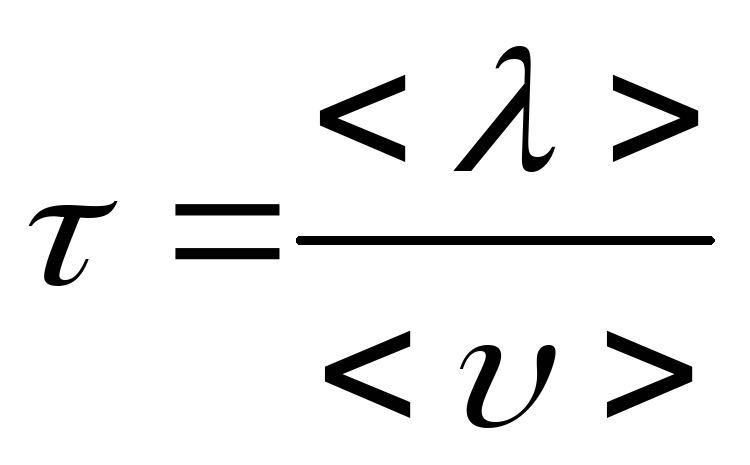. Поэтому средняя частота столкновений (среднее число столкновений за одну секунду) равна 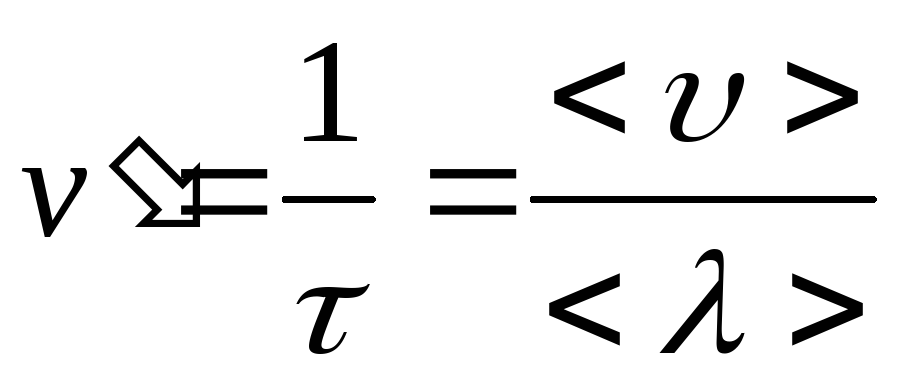. В течение времени число молекул из данного объема в результате столкновений летят изотропно по всевозможным направлениям, в том числе и в направлении площадки , которая видна из элемента объема под углом . Число молекул, пересекших площадку и на пути от элемента объема не испытавших ни одного последующего столкновения, равно:

, (1)

где – множитель, который учитывает выбывание молекул из пучка из-за столкновений с другими молекулами;

–множитель, который определяет число молекул, приходящихся на данный телесный угол;

–расстояние от объема до центра площадки .

Поток числа молекул, пересекающих поверхность в единицу времени, равен:

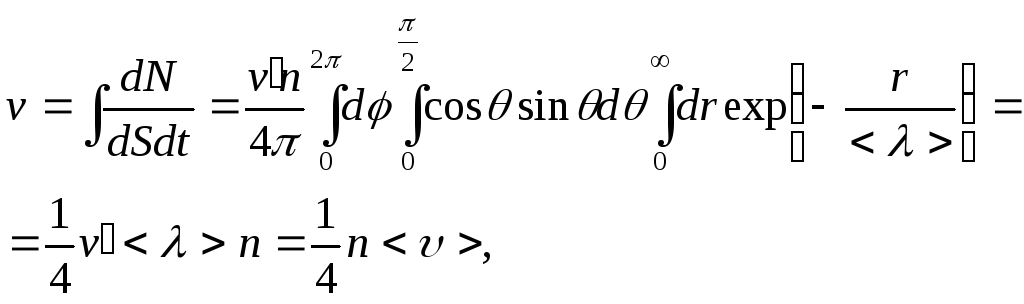(2)

где – концентрация молекул вещества,

–средняя скорость молекул вещества,

–среднее число столкновений в секунду,

–средняя длина свободного пробега.

Теперь вычислим среднее расстояние вдоль оси , которое проходят молекулы, пересекающие площадку после последнего столкновения. Из теории вероятности известно, что среднее значение непрерывно изменяющейся величины равно

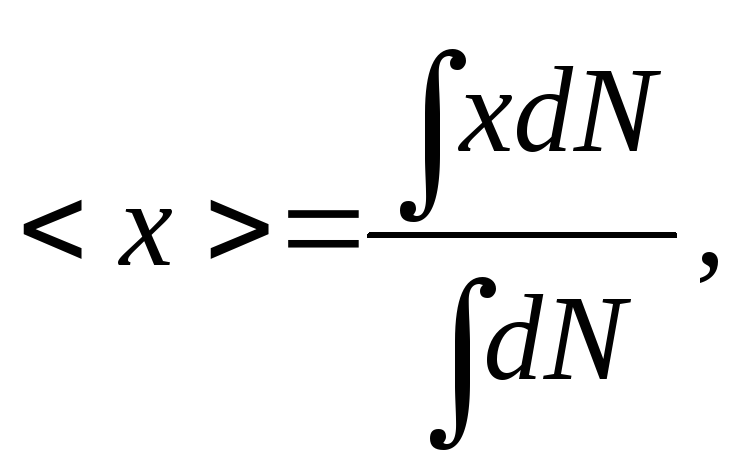(3)

где дается формулой (1). В результате интегрирования (3) выражение для среднего расстояния, пробегаемого молекулами, пересекающими площадку (рис.1) после последнего столкновения примет вид:

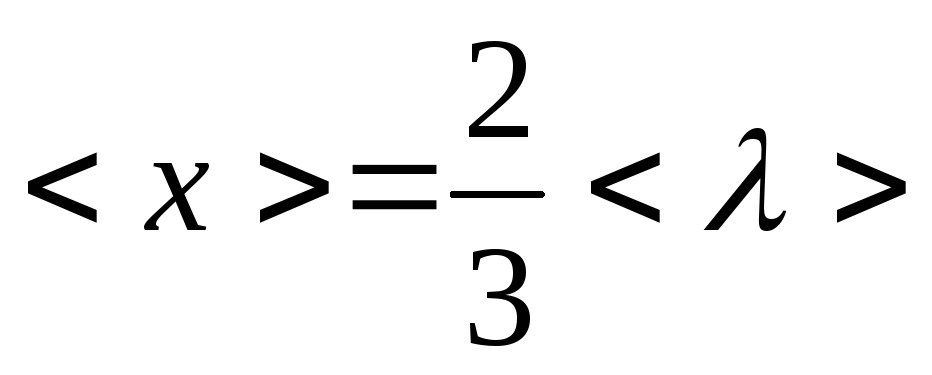, (4)

где – средняя длина свободного пробега молекулы.

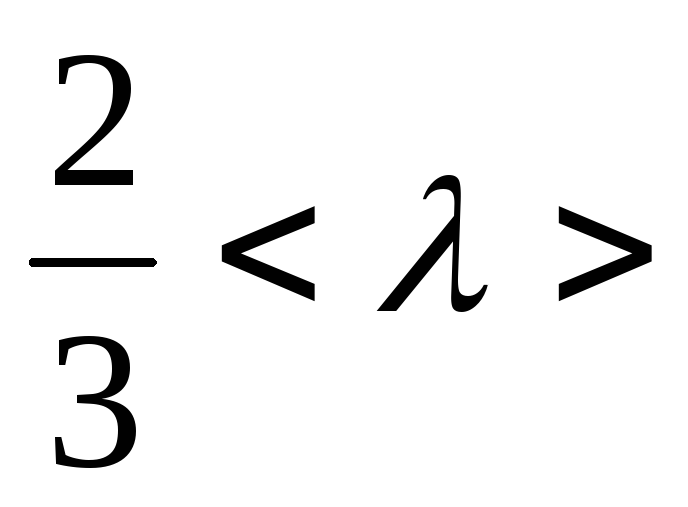Запишем на расстоянии от площадки с учетом того, что эта величина в большинстве случаев достаточно мала и ограничившись первым членом разложения в ряд Тейлора в точке :

. (5)

Поток числа молекул в направлении оси , согласно формуле (2) равен . Следовательно, поток сквозь площадку в направлении отрицательных значений оси равен

, (6)

а в направлении положительных значений оси дается выражением

, (7)

Следовательно, суммарный поток в положительном направлении оси в точке имеет вид

, (8)

где – концентрация молекул вещества,

–средняя скорость молекул вещества,

–средняя длина свободного пробега молекулы,

–частная производная величины по .

Уравнение (8) является основным уравнением процессов переноса количества .

Здесь использован символ частной производной, поскольку величина зависит и от времени и от координаты .

Выражение (8) можно легко обобщить на случай трехмерного пространства:

, (9)

где , (10)

где – единичные векторы, направленные по осям прямоугольной системы координат;

–единичный вектор, направленный по нормали в сторону возрастания .