
- •3 Время регулирования, перерегулирования и колебательность
- •4 Выбор частоты среза и наклона жлачх в области частоты среза
- •5 Высокочастотный участок лачх – влияние на переходные процессы и качество системы
- •6 Вычисление основных показателей качества по распределению корней
- •7 Вычисление статической ошибки
- •9 Зависимость показателей качества от расположения корней характеристического уравнения на комплексной плоскости
- •10 Квадратичная интегральная оценка
- •11 Метод гармонической линеаризации
- •13 Метод фазовой плоскости
- •14 Методы исследования нелинейных систем
- •15 Модальное управление
- •16 Нелинейные системы
- •17 Низкочастотный участок лачх – влияние на переходные процессы и качество системы
- •V порядок астатизма
- •18 19 20
16 Нелинейные системы
Нелинейной называется такая САУ, у которой зависимость между входными и выходными переменными одного или нескольких элементов описывается нелинейными уравнениями.
Все реальные элементы и системы, строго говоря нелинейны, и к понятию линейной системы приходят путем линеаризации. Но на практике встречаются такие нелинейные элементы, к которым операция линеаризации по малому отклонению не применима. Такие нелинейности называют существенными.
Прежде всего, к нелинейным дифференциальным уравнениям не применим принцип суперпозиции. Нелинейные дифференциальные уравнения не имеют каких — либо общих методик решения. Для исследования нелинейных дифференциальных уравнений нельзя использовать аппарат преобразований Лапласа и Фурье.
Судить об устойчивости решений нелинейных дифференциальных уравнений на основании теорем Ляпунова, по дифференциальным уравнениям линеаризованных систем, можно только при малых отклонениях от установившегося движения, т е. можно судить только об устойчивости в малом. Между тем, нелинейная система, устойчивая в малом, может быть неустойчивой при больших отклонениях. Различают, кроме устойчивости в малом, следующие виды устойчивости нелинейных систем.Система называется устойчивой в большом, если она устойчива при больших конечных по величине отклонениях. Система называется устойчивой в целом, если она устойчива при любых, не ограниченных по величине, начальных отклонениях. Если система асимптотически устойчива в целом, то ее называют абсолютно устойчивой.
Особенностью нелинейных систем является возникновение в них, при некоторых начальных условиях, гармонических колебаний с определенной амплитудой и частотой, так называемых предельных циклов. Если предельный цикл устойчив, т.е. к нему сходятся все траектории сверху и снизу в определенном диапазоне начальных условий, то он называется автоколебаниями. Амплитуда и частота автоколебаний зависят только от параметров системы.
17 Низкочастотный участок лачх – влияние на переходные процессы и качество системы
Низкочастотная
часть ЛАЧХ желаемой системы влияет на
статику системы, т.е. она определяется
требуемой точностью работы системы, а,
следовательно, коэффициентом усиления
системы и порядком ее астатизма.
Низкочастотный участок желаемой ЛАЧХ
проводят, как правило, с наклоном
 дб/дек
и если исходная система отвечает
требованиям задания по точности, то
низкочастотный участок желаемой ЛАЧХ
оставляют совпадающим с низкочастотным
участком исходной ЛАЧХ.
дб/дек
и если исходная система отвечает
требованиям задания по точности, то
низкочастотный участок желаемой ЛАЧХ
оставляют совпадающим с низкочастотным
участком исходной ЛАЧХ.
V порядок астатизма
18 19 20
Прежде всего, выбираем типовую ВЧХ замкнутой САУ, отвечающую требуемым показателям качества. На рис. 9 изображена типовая трапецеидальная ВЧХ, которую можно реализовать, используя корректирующее звено наиболее простой структуры.

Рис. 9. Типовая трапецеидальная ВЧХ замкнутой системы.
Типовая ВЧХ описывается следующими параметрами:
 —коэффициент
наклона;
—коэффициент
наклона;
 —дополнительный
коэффициент наклона;
—дополнительный
коэффициент наклона;
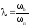 —коэффициент
формы;
—коэффициент
формы;
 —интервал
положительности.
—интервал
положительности.
Pmax и Pmin—максимальное и минимальное значения ВЧХ.
Из
рассмотрения заранее построенных кривых
переходных процессов для различных
коэффициентов
 ,
, 1
и λ было
установлено, что лучшие переходные
процессы соответствуют ВЧХ с коэффициентами
1
и λ было
установлено, что лучшие переходные
процессы соответствуют ВЧХ с коэффициентами
 ≤ 0,8,
≤ 0,8, 1
≥ 0,4, λ ≥0,5.
Величина перерегулирования σmax
в этом случае определяется в основном
значением Pmax.
Для связи параметров переходного
процесса (tр
– времени регулирования и σ –
перерегулирования) с параметрами ВЧХ
замкнутой САУ (Pmax
– максимальным значением и ωп
– частотой положительности) существуют
специальные номограммы перевода (рис.
10).
1
≥ 0,4, λ ≥0,5.
Величина перерегулирования σmax
в этом случае определяется в основном
значением Pmax.
Для связи параметров переходного
процесса (tр
– времени регулирования и σ –
перерегулирования) с параметрами ВЧХ
замкнутой САУ (Pmax
– максимальным значением и ωп
– частотой положительности) существуют
специальные номограммы перевода (рис.
10).

Рис.
10. Графики зависимости времени
регулирования tр
и
перерегулирования σ от максимального
значения Pmax
ВЧХ при
 ≤ 0,8,
≤ 0,8, 1
≥
0,4, λ ≥0,5.
1
≥
0,4, λ ≥0,5.
Отрицательная часть ВЧХ влияет на перерегулирование, увеличивая его на величину:
 .(4.1)
.(4.1)
Увеличение перерегулирования можно учесть, положив (при этом кривые с индексами Pmin и Pmax на рис. 11 будут располагаться симметрично):
 .(4.2)
.(4.2)
Затем по Pmax по рис. 9 определяем зависимость между tр и ωп. По заданному tр определяем ωп.
После нахождения основных величин для типовой ВЧХ – ωп, Pmax и Pmin – можно переходить к формированию желаемой ЛАЧХ.
Очевидно, что
Pmin ≤ P(ω) ≤ Pmax.(4.3)
С помощью номограммы перевода ЛАФХ разомкнутой САУ в ВЧХ замкнутой САУ (рис. 11) можно определить требование к желаемой ЛАЧХ.
Последнее условие эквивалентно требованию, чтобы ЛАФХ не заходила в запретную область, ограниченную кривыми с индексами Pmin и Pmax. Можно заменить это условие более жестким, но и более простым: АФХ не должна заходить в прямоугольник, охватывающий две эти кривые. Чтобы ЛАФХ не попадала внутрь указанного прямоугольника, одновременно должны выполняться условия в определенном интервале частот:

L2 ≤ Lж(ω) ≤ L1
φж(ω) > φ1,(4.4)
где
φ1 – вертикаль прямоугольника, охватывающего кривые с индексами Pmin и Pmax на рис. 10;
L1 и L2 – соответственно верхняя и нижняя горизонталь прямоугольника;

Рис. 11. Номограмма для перевода логарифмической АФХ разомкнутой системы в ВЧХ замкнутой системы
