2 Образец выполнения контрольной работы

Задание 1

Дана система линейных алгебраических уравнений (СЛАУ)

Требуется:

1) Решить слау по формулам Крамера;

2) Записать слау в матричной форме и решить ее матричным способом;

3) Решить слау методом Гаусса.

Решение

1. Решим систему по формулам Крамера:

,

где главный определитель системы, составленный из коэффициентов при неизвестных;

определитель системы, полученный путем замены -го столбца главного определителя системы столбцом свободных членов.

Таким образом, , , .

2 Решим СЛАУ матричным способом.

Обозначим:

; ; .

Тогда данную систему можно записать в виде откуда (обратная матрица по отношению к матрице ₎.

Найдем по следующей формуле:

,

где − алгебраические дополнения к соответствующим элементам матрицы А: , (миноры, соответствующие элементам матрицы А).

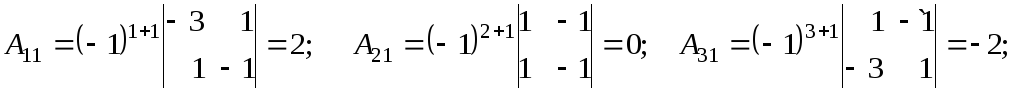
Обратная матрица имеет вид:

.

Тогда.

Итак, решение системы:

3 Решим СЛАУ методом Гаусса.

С помощью элементарных преобразований строк расширенную матрицу системы приведем к следующему виду:

Так как , то система совместна и имеет решение. Полученной матрице соответствует система

которая эквивалентна исходной. Из данной системы следует, что

Ответ:

Задание 2

Даны вершины треугольника АВС: А(-2; -2), В(1; 7), С(11; 3). Найти:

1) уравнение стороны АВ;

2) уравнение высоты СН и ее длину;

3) уравнение медианы АМ и ее длину;

4) точку N пересечения медианы АМ и высоты СН;

5) уравнение прямой, проходящей через вершину С параллельно стороне АВ;

6) внутренний угол при вершине А.

Решение

1 Уравнение прямой, проходящей через две точки , имеет вид:

Тогда - уравнение прямой (стороны) АВ.

2 Уравнение высоты СН получим, воспользовавшись уравнением прямой, проходящей через точку параллельно вектору

.

Так как , то нормальный вектор является направляющим для прямой СН, т.е. Следовательно, уравнение стороны СН.

Длину высоты СН найдем как расстояние от точки С до прямой АВ, используя формулу

где уравнение данной прямой;

координаты данной точки.

Имеем:

3 Так как АМ – медиана, то точка М – середина отрезка ВС. Координаты середины отрезка находим по формулам:

Тогда

Уравнение прямой АМ:

Длину медианы АМ найдем как расстояние между двумя точками, используя формулу

где

Имеем

4 Найдем точку N пересечения медианы АМ и высоты СН, решив систему:

Тогда и N=

5 Так как прямая, проходящая через точку С параллельно прямой АВ, имеет тот же нормальный вектор, что и прямая АВ, т.е. то уравнение прямой СЕ запишем, используя уравнение прямой, проходящей через точку перпендикулярно нормальному вектору

Следовательно, уравнение стороны АВ.

6 Для нахождения внутреннего угла А воспользуемся формулой

Так как , то

Следовательно,

Ответ: 1) АС: 2) СН:

3) АМ: 4) N 5) СЕ:

6)

Задание 3

Найти пределы функций:

а) б) ; в) ;

г) .

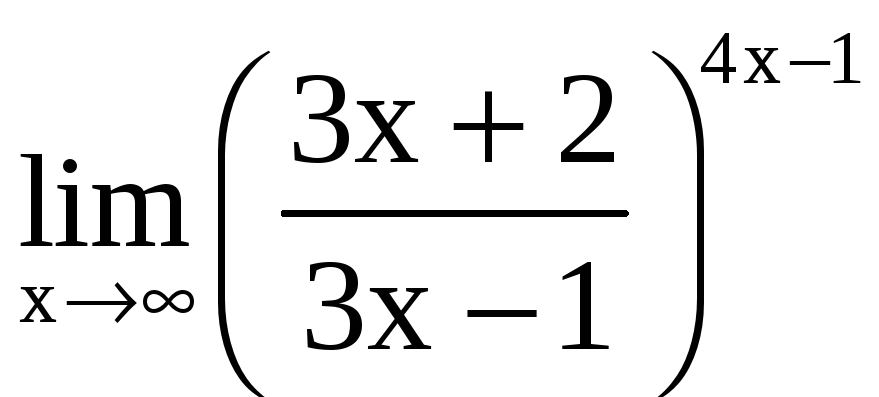Решение

а)

б)

в)

=;

г)

Ответ: а) ; б) 3; в) ; г) .

Задание 4

Найти:

а) производную и дифференциал функции в точке ; б) при помощи логарифмического дифференцирования производную функции ;

в) производную функции , заданной неявно уравнением .

Решение

а) Принимая за u и применяя формулу , имеем . При получаем .

Дифференциал функции находим по формуле . Тогда , ;

б) Логарифмируя обе части исходного равенства, получаем

или .

Дифференцируя полученное соотношение по , имеем

Отсюда

;

в) дифференцируя заданное соотношение, рассматривая как функцию от , получаем

.

Решаем полученное уравнение относительно :

.

Ответ: а) , ; б) ;

в) .

Заданиие 5

Исследовать методами дифференциального исчисления функцию и построить ее график.

Решение

Для исследования функции и построения ее графика применяется следующая схема:

1. найти область определения функции;

2. определить точки разрыва функции и выяснить их характер;

3. исследовать функцию на четность и нечетность, периодичность;

4. найти точки пересечения графика функции с осями координат;

5. найти асимптоты графика функции;

6. найти промежутки возрастания и убывания, точки экстремума;

7. найти интервалы выпуклости и вогнутости, точки перегиба;

8. для уточнения графика найти дополнительные точки;

9. по результатам исследования построить график функции.

Применим вышеуказанную схему для исследования данной функции:

1) область определения функции ;

2) функция не определена в точке . Следовательно, есть точка разрыва функции. Исследуем характер точки разрыва, для чего найдем односторонние пределы функции в этой точке:

.

Следовательно, точка разрыва второго рода;

3) функция не является ни четной, ни нечетной, так как

;

4) найдем точки пересечения с осью Ох, решив уравнение :

.

Точка – точка пересечения графика с осью Ох.

Точки пересечения с осью Оy найдем, положив : . Точка (0; –1) – точка пересечения графика с осью Оу;

5) так как точка – точка разрыва второго рода, то прямая – вертикальная асимптота.

Найдем наклонные асимптоты вида , где

, .

Тогда

Следовательно, – горизонтальная асимптота;

6) определим промежутки возрастания, убывания функции и точки экстремума, для чего найдем критические точки первого рода:

Так как при , следовательно является критической (стационарной) точкой. Других критических точек нет, так как точка , в которой функция имеет бесконечную производную, не принадлежит .

Полученные данные занесем в таблицу 7.

Таблица 7

x		0		1
		0	+		
y	Убывает		Возрастает	Не существует	Убывает

Функция убывает на интервалах и возрастает на интервале . Следовательно, точка есть точка минимума;

7) определим промежутки выпуклости, вогнутости и точки перегиба, для чего найдем критические точки второго рода:

при , следовательно является критической точкой. Других критических точек нет, так как точка , в которой функция имеет бесконечную вторую производную, не принадлежит . Полученные данные занесем в таблицу 8.

Таблица 8

x				1
		0	+		+
y	Выпукла		Вогнута	Не существует	Вогнута

Функция выпукла на интервале и вогнута на интервалах . Точка есть точка перегиба графика функции;

8) для уточнения графика найдем дополнительные точки:

;

9) по полученным данным строим график функции (рисунок 1).

Рисунок 1 – График функции

Задание 6

a), б) Найти неопределенный интеграл;

в) вычислить определенный интеграл.

Решение

а) ;

б) воспользуемся формулой интегрирования по частям .

в)

.

Ответ: а) ; б); в) .

Задание 7

Дана функция , точки и . Найти:

1) частные производные и полный дифференциал данной функции;

2) производную функции в точке по направлению вектора и градиент функции в точке

Решение

1. Найдем частные производные данной функции:

Полный дифференциал функции находится по формуле

Тогда .

2. Производная функции в точке по направлению вектора вычисляется по формуле

где , направляющие косинусы вектора

Если то

Тогда

Следовательно,

3 Градиент функции () вычисляется по формуле

Тогда

Вопросы к экзамену

1 Матрицы. Примеры специальных матриц. Арифметические операции над матрицами. Транспонирование матриц.

2 Элементарные преобразования строк (столбцов) матрицы. Ранг матрицы. Вычисление ранга матрицы с помощью элементарных преобразований.

3 Определители 2-го и 3-го порядка, их свойства.

4 Миноры и алгебраические дополнения. Вычисление определителей по строке (столбцу).

5 Обратная матрица. Построение обратной матрицы. Матричный способ решения СЛАУ.

6 Решения СЛАУ с помощью формул Крамера.

7 Решения СЛАУ методом Гаусса.

8 Теорема Кронекера-Капелли. Базисные решения СЛАУ. Однородные СЛАУ.

9 Векторы. Линейные операции над векторами. Коллинеарность, компланарность векторов. Проекция вектора на ось. Угол между векторами.

10 Линейная зависимость и независимость векторов и линейная комбинация. Базис. Разложение вектора по базису.

11 Декартова прямоугольная система координат. Разложение вектора в ортонормированном базисе. Длина вектора. Направляющие косинусы.

12 Скалярное произведение двух векторов, его свойства. Скалярное произведение векторов, заданных в координатной форме.

13 Различные виды уравнений прямой на плоскости.

14 Условия параллельности и перпендикулярности прямых на плоскости. Угол между двумя прямыми. Расстояние от точки до прямой.

15 Прямая в пространстве. Канонические и параметрические уравнения прямой.

16 Общее уравнение плоскости. Уравнение плоскости в отрезках. Условия параллельности и перпендикулярности двух плоскостей. Угол между двумя плоскостями.

17 Условия параллельности и перпендикулярности прямой и плоскости. Расстояние от точки до плоскости. Угол между прямой и плоскостью.

18 Числовая последовательность и ее предел. Основные свойства сходящихся последовательностей.

19 Предел функции. Замечательные пределы.

20 Бесконечно малые (б.м.ф.) и бесконечно большие функции (б.б.ф). Свойства б.м.ф. и б.б.ф. Эквивалентные б.м.ф. и их применение при вычислении пределов.

21 Непрерывность функции в точке. Классификация точек разрыва.

22 Производная функции одной переменной, ее смысл в различных задачах физики, геометрии, экономики.

23 Дифференцируемость функции в точке. Дифференциал функции одной переменной. Геометрический смысл дифференциала.

24 Таблица производных основных элементарных функций. Основные правила дифференцирования.

25 Производные высших порядков.

26 Экстремумы функции одной переменной. Необходимое условие экстремума.

27 Достаточные условия экстремума функции одной переменной.

28 Выпуклость, вогнутость графика функции. Точки перегиба графика функции.

29 Асимптоты графика функции. Схема исследования функции и построение графика.

30 Первообразная и неопределенный интеграл. Свойства неопределенного интеграла.

31 Таблица основных неопределенных интегралов.

32 Интегрирование методом замены переменной и по частям.

33 Определение определенного интеграла, его основные свойства.

34 Формула Ньютона-Лейбница.

35 Вычисление определенного интеграла методом замены переменной и по частям.

36 Несобственные интегралы.

37 Приложения определенного интеграла в экономических задачах.

38 Приближенное интегрирование (формула прямоугольников, трапеций, Симпсона).

39 Определение функции нескольких переменных (ФНП). Геометрическое изображение функции двух переменных. Линии уровня.

40 Частные производные ФНП. Дифференцируемость ФНП в точке. Дифференциал ФНП.

41 Производная по направлению. Градиент функции.

42 Частные производные и дифференциалы высших порядков ФНП.

43 Экстремум функции нескольких перемененных. Необходимое и достаточные условия существования экстремума.

44 Условный экстремум ФНП. Метод множителей Лагранжа.

45 Метод наименьших квадратов. Случай линейной зависимости.

Список литературы

1. Жевняк, Р. М. Высшая математика: Основы аналитической геометрии и линейной алгебры. Введение в анализ. Дифференциальное исчисление функции одной переменной / Р. М. Жевняк, А. А. Карпук. – Минск: Выш.шк.,1992. – 384 c.

2. Гусак, А. А. Справочник по высшей математике / А. А. Гусак, Г. М. Гусак. – Минск: Навука i тэхнiка, 1991. – 479 c.

3. Белько, И. В. Высшая математика для экономистов. Экспресс-курс / И. В. Белько, К. К. Кузьмич.– М.: Новое знание, 2002. –144 с.

4. Унсович, А. Н. Краткий курс высшей математики для экономистов / А. Н. Унсович.– Барановичи: БНИП, 2000. – 531 с.

5 Минюк С. А. Высшая математика для экономистов / С. А. Минюк, С. А. Самаль, Л. И. Шевченко. – Минск: Элайда, 2003. – Т.1. – 525 c.