-
Оценки математического ожидания и дисперсии случайной величины х.
Для математического ожидания
выборочное среднее находим по формуле:
Для дисперсии
находим
исправленную дисперсию:
Дисперсию рассчитываем по формуле
-
Доверительные интервалы для математического ожидания и дисперсии соответствующей заданной доверительной вероятности (1-)=0,95.
Доверительная вероятность (1-)=0,95, тогда по таблице значений функции Лапласа находим =1,96, следовательно, доверительные интервалы будут иметь вид:
-для математического ожидания:
M1<MX<M2
М1=0,81; М2=1,03
0,81<MX<1,03
-для дисперсии:
D1<DX<D2
D1=0,79; D2=1,38
0,79<DX<1,38
-
Вероятность попадания случайной величины х в заданный интервал [0,7, 1).
Находим точечную
оценку вероятности попадания случайной
величины Х в интервал [0,7, 1)
=
[0,58, 0,83). Так как в этот интервал попало
m =51 экспериментальных
значений, то искомая оценка будет равна:
-
Доверительный интервал для
(x)=0,1,
соответствующий заданной доверительной
вероятности (1-)
= 0,9.
Доверительная вероятность (1-)=0,9, тогда по таблице значений функции Лапласа находим =1,65. Для вероятности Р=0,1 доверительный интервал имеет вид:
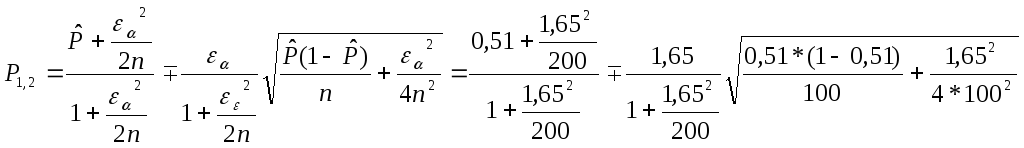
P1=0,43; P2=0,60
-
Построение гистограммы и эмпирической функции распределения случайной величины х.
Для построения гистограммы Г(х) заключаем все экспериментальные данные в интервал (700,1360)и разбиваем его на 12 равных разрядов каждый длиной в 55.
|
Разряд (Хi-1,Xi) |
ni |
Частота попадания случайной величины Х в разряд (Хi-1,Xi) |
Значение гистограммы Г(х) |
|
(700, 755) |
1 |
0,01 |
0,00018 |
|
(755,810) |
2 |
0,02 |
0,00036 |
|
(810,865) |
3 |
0,03 |
0,00055 |
|
(865,920) |
14 |
0,14 |
0,00255 |
|
(920,975) |
19 |
0,19 |
0,00345 |
|
(975,1030) |
22 |
0,22 |
0,00400 |
|
(1030,1085) |
17 |
0,17 |
0,00309 |
|
(1085,1140) |
16 |
0,16 |
0,00291 |
|
(1140,1195) |
3 |
0,03 |
0,00055 |
|
(1195,1250) |
1 |
0,01 |
0,00018 |
|
(1250,1305) |
1 |
0,01 |
0,00018 |
|
(1305,1360) |
1 |
0,01 |
0,00018 |
Таблица 1
значение гистограммы Г(x) (Таблица 1):
,
где
- число экспериментальных точек, попавших
в этот разряд
,
а
- его длина. (Рис.1)
частоты попадания экспериментальных точек в разряды гистограммы:
Соответствующую эмпирическую функцию рассчитываем по формуле:
;
где
- число экспериментальных точек, лежащих
левее х. (Рис.3)
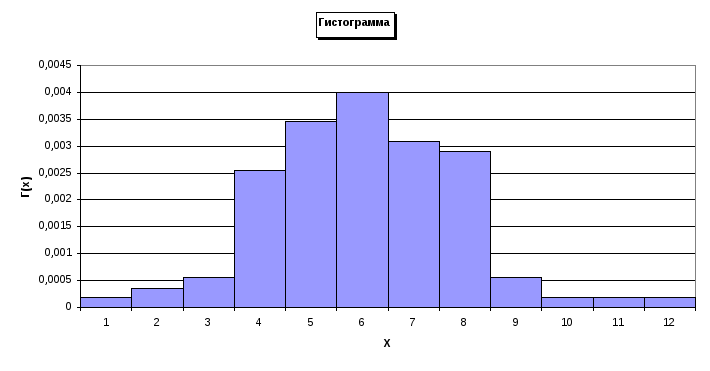Рис
1
-
Найти и построить доверительные области для плотности распределения f(X) и функции распределения f(X), соответствующие заданной доверительной вероятности
f(x) 1-=0,95
F(x) 1-=0,8.
а) На каждом
разряде
находим доверительную область
для
вероятности
попадания исходной величины X
в этот разряд. Вычисляем по формуле
(пункт 4.) с заменой величины
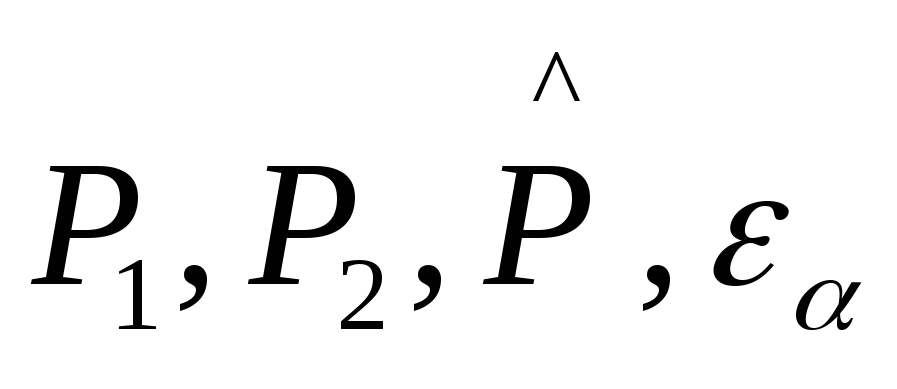соответственно на
.
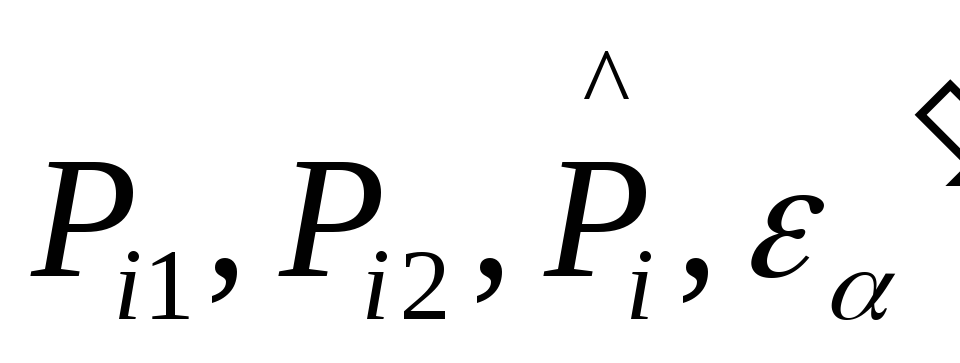В данном случае общее число разрядов r
= 12 плюс 2 полу бесконечных разряда , r
= 14. Выбираем доверительную вероятность
(1-
),
равную 0,95 , из условия:
и,
используя таблицу значений функции
Лапласа, находим
=
2,915.
i = 1...r
плотность
на
i-ом разряде;
доверительные
границы для плотности
,
которая находится по формуле:
,
;
длина разряда (Таблица 2),(Рис 2).
б) Графической оценкой функции распределения F(x) является эмпирическая функция распределения:
,
где
- число экспериментальных точек, лежащих
левее x.
По таблице
распределения величины
(распределение Колмогорова) находим ее
величину, соответствующую коэффициенту
доверия (1-) = 0,8. Она
равна
=1,07.
Затем рассчитываем доверительную
область для функции распределения F(x):
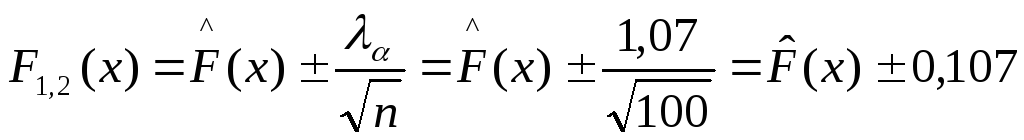(Рис.3).
-
разряд
доверительные границы для плотности распределения f(x)
0
0
0,00148
0
0
0,00148
(700, 755)
0,00002
0,00181
(755,810)
0,00006
0,00212
(810,865)
0,00012
0,00240
(865,920)
0,00127
0,00510
(920,975)
0,00193
0,00618
(975,1030)
0,0235
0,00681
(1030,1085)
0,00166
0,00575
(1085,1140)
0,00153
0,00554
(1140,1195)
0,00012
0,00240
(1195,1250)
0,00002
0,00181
(1250,1305)
0,00002
0,00181
(1305,1360)
0,00002
0,00181
0
0
0,00148
0
0
0,00148
Таблица 2
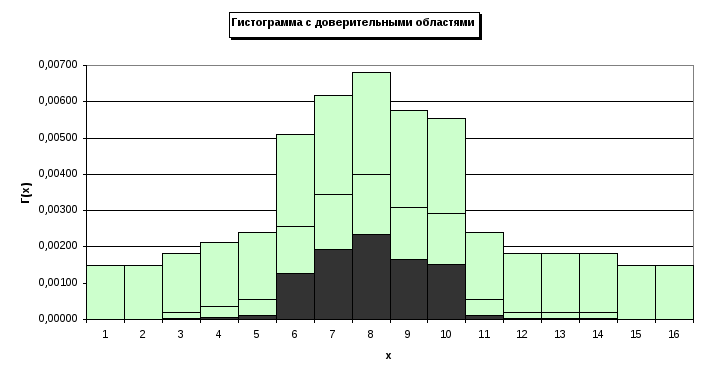
Рис.2
Рис.3