
2.2. Методологические и методические основы прогнозирования
Для изучения любой дисциплины необходимо знать ее методологию. Методология научного экономического предвидения включает совокупность принципов, методов и показателей, применяемых в процессе прогнозирования и планирования.
Принцип прогнозирования характеризует основное исходное положение или идею теории. К основным принципам прогнозирования относятся: системность, согласованность, вариантность, непрерывность, верифицируемость, т. е. определение достоверности, и эффективность.
Системность в прогнозировании означает требование взаимоувязанности и соподчиненности объекта, фона и элементов прогнозирования. Согласованность в прогнозировании означает необходимость согласования поисковых и нормативных прогнозов различной природы (признаков) и различного срока упреждения времени. Вариантность в прогнозировании означает требование разработки вариантов прогнозов, исходя из вариантов прогнозного фона. Принцип непрерывности заставляет производить корректировку прогноза по мере поступления новой информации об объекте прогнозирования. Верифицируемость означает потребность в достоверности, точности и обоснованности прогноза. Эффективность (или рентабельность) прогнозирования определяет необходимость превышения экономического эффекта от использования прогноза над затратами по его разработке.
Основные исходные положения теории прогнозирования не исчерпываются указанными принципами. Определенные требования предъявляются и к разработке отдельных элементов прогноза. Так, один из элементов прогнозирования — анализ — должен проводиться с учетом таких принципов, как природная специфичность, оптимизация описания объекта прогнозирования, аналогичность и др.
В прогнозировании большое значение имеет выбранный метод, а также прием. Прием прогнозирования - это одна или несколько математических или логических операций, направленных на получение конкретного результата при прогнозировании. В качестве примеров таких приемов можно назвать сглаживание или выравнивание динамического ряда, расчет средневзвешенного значения величин. Метод прогнозирования — это способ исследования объекта прогнозирования, направленный на разработку прогноза. Совокупность специальных правил, приемов и методов составляет методику прогнозирования.
К наиболее распространенным методам прогнозирования относятся: экстраполяция, нормативные расчеты, в том числе интерполяция, экспертные оценки, аналогия, математическое моделирование.
Экстраполяция — это метод, при котором прогнозируемые показатели рассчитываются как продолжение динамического ряда на будущее по выявленной закономерности развития. По сути, экстраполяция является переносом закономерностей и тенденций прошлого на будущее на основе взаимосвязей показателей одного ряда. Метод позволяет найти уровень ряда за его пределами, в будущем. Экстраполяция эффективна для краткосрочных прогнозов, если данные динамического ряда выражены ярко и устойчиво.
Рассмотрим несложные примеры экстраполяции в экономическом прогнозировании.
Пример1. Составить прогноз продажи хлебобулочных изделий в магазине на 11-й день его работы. Известно, что за прошедшие 10 дней работы объем продажи хлебобулочных изделий в магазине составил (в тоннах), табл. 1.
Таблица 1
Объем продаж хлебобулочных изделий за один день работы магазина
|
1-й день |
2-й день |
3-й день |
4-й день |
5-й день |
6-й день |
7-й день |
8-й день |
9-й день |
10-й день |
|
2,5 |
2,8 |
2,0 |
2,4 |
2,3 |
2,9 |
2,7 |
2,2 |
2,3 |
2,8 |
Расчет. Учитывая определенную стабильность потребления товара, составим прогноз продажи на основе его среднего объема реализации за день, т. е. по формуле средней арифметической:
Q= Q1+Q2+Q3+...Qn (1)
п
где Q1.2.3...n — объем продажи хлебобулочных изделий за каждый день работы, т; п — число дней периода. Тогда Q = (2,5 + 2,8 + 2,0 + 2,4 + 2,3 + 2,9 + 2,7 + 2,2 + 2,3 + + 2,8): 10 = = 2,49 т (или около 2,5 т в день).
Таким образом, экстраполяция продажи хлебобулочных изделий в магазине показала, что на 11-й день работы, равно как и на 12-й и 13-й дни работы, продажа товара может составить 2,5 т. Можно рассчитать среднюю ошибку прогноза по формуле:
 (2)
(2)
где μ - средняя ошибка; σ - дисперсия, определяемая по формуле
 (3)
(3)
Средняя ошибка прогноза составит 0,026 т
Вывод. Прогноз ежедневной продажи составляет 2,5 т и при неизменности формирующих спрос данных может иметь отклонение ±0,081т.
Понятно, что такой прогноз будет справедлив, если в ближайшем будущем не закроется на ремонт соседняя булочная или не будет введен в эксплуатацию недалеко от магазина новый многоквартирный дом.
Пример 2. Составить прогноз объема платных услуг в фирме на 2007 и 2001 гг. Известно, что в 2000 г. объем платных услуг в фирме составлял 207 денежных единиц (д. ед.), а в 2006 г. — 228 д. ед. в сопоставимых ценах. Сложившиеся условия работы фирмы существенно не изменятся.
Расчет. Для определения прогноза методом экстраполяции по сложившемуся приросту объема услуг надо определить его среднегодовой рост за прошедшие годы и экстраполировать на будущие периоды. Рассчитаем среднегодовой темп роста (коэффициент) по формуле:
 ,
(4)
,
(4)
где
 – среднегодовой
темп роста;
– среднегодовой
темп роста;
n — число периодов динамического ряда;
уn — объем платных услуг в отчетном году, д. ед.;
y0— объем платных услуг в базисном году, д. ед.
Среднегодовой темп роста спроса на платные услуги фирмы составит:

 или 102,44%
или 102,44%
Соответственно прогноз объема услуг составит: на 2007 г. 228 х 1,0244 = 233,6 д. ед.; на 2008 г. 233,6 х 1,0244 = 239,3 д. ед.
Вывод. Прогноз объема услуг в фирме составит: на 2007 г – 233,6 д. ед., на 2008г - 239,3 д. ед.
Приведенные примеры использования метода экстраполяции в прогнозировании далеко не исчерпывают его обширные возможности. Если предполагается сохранение прошлых и настоящих тенденций развития на будущее, то говорят о формальной экстраполяции. Если же фактическое развитие увязывается с гипотезами о динамике процесса развития с учетом физической и логической сущности, то говорят о прогнозной экстраполяции. Прогнозная экстраполяция может быть в виде тренда, огибающих кривых, корреляционных и регрессионных зависимостей, может быть основана на факторном анализе и др. Экстраполяция сложного порядка может перерасти в моделирование.
Для такого вида экстраполяции, как тренд, характерно нахождение плавной линии, отражающей закономерности развития во времени. Тренд обычно применяется как основная составляющая прогнозируемого временного ряда, на которую накладываются другие составляющие, например сезонные колебания. Экстраполяция на основе тренда включает:
-
сбор информации эмпирического ряда показателя за прошлые периоды;
-
выбор оптимального вида функции, описывающей указанный ряд с учетом его сглаживания и выравнивания;
-
расчет параметров выбранной экстраполяционной функции;
-
расчет прогноза на будущее по выбранной функции.
Экстраполяция на основе тренда показана в примере 3.
Пример 3. Составить прогноз спроса на кожаную обувь на 2007г., используя метод экстраполяции динамического (временного) ряда.
Известны данные о продаже населению товара за последние 5 лет (в денежных единицах):
2001г.- 179,3
2002г.- 193,3
2003г.- 206,0
2004г.- 216,9
2005г.- 226,6
Расчет. Построим график продажи кожаной обуви в регионе за последние 5 лет (рис. 2).
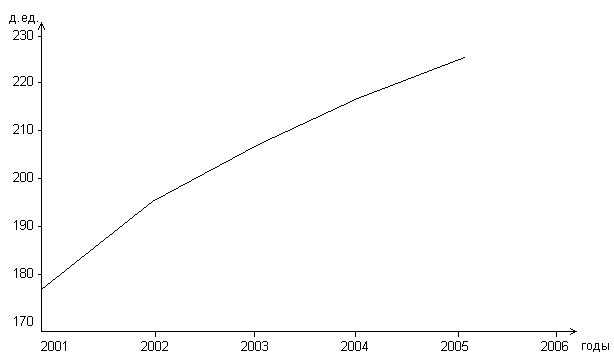
Рис.2. Динамика товарооборота кожаной обуви в регионе за 5 лет
Линия объема продаж обуви по годам близка к линейной зависимости, которая выражается формулой (5), т.е. выглядит как:
y=a+bx; (5)
где: y – объем товарооборота (спрос);
х – годы;
а – параметр, характеризующий влияние основных факторов на продажу кожаной обуви (цены, денежных доходов населения, товарного обеспечения и др.);
b – параметр, характеризующий влияние вспомогательных факторов на продажу кожаной обуви (погоды, моды, сезонности, режима работы предприятий торговли и др.).
Для нахождения параметров необходимо решить систему уравнений способом наименьших квадратов;
Σy=an+bΣx (6)
Σxy=aΣx+bΣx2
Для этого необходимо провести дополнительные расчеты, которые приведены в таб. 2
Таблица 2
Данные о продаже кожаной обуви в регионе для нахождения параметров прямой спроса
|
Годы x |
спрос y |
xy |
x2 |
|
1 2 3 4 5 |
179,3 193,3 206,0 216,9 226,6 |
179,3 286,6 618,0 867,6 1133,0 |
1 4 9 16 25 |
|
Итого 15 |
1022,1 |
3184,5 |
53 |
Тогда система уравнений будет иметь вид:
1022,1=5а+15в
3184,5=15а+55в
а=168,96 в=11,82
y=168,96+11,82х
По найденному уравнению можно провести расчеты тренда, т.е. определить выровненные значения спроса за прошлые годы и рассчитать прогноз на будущее. Так, для прогноза на 7-й год необходимо в полученное уравнение подставить очередной год-7:
y=168,96+11,82*7=251,7 д.ед.
Вывод. Спрос на кожаную обувь в 2007г. может составить 251,7 д.ед. (в ценах 2005 г.)
При нормативном методе прогнозирования определяются пути и сроки достижения возможных состояний явления, принимаемых в качестве цели. Речь идет о прогнозировании достижения желательных состояний явления на основе заранее заданных норм, идеалов, стимулов и целей. Такой прогноз отвечает на вопрос: какими путями можно достичь желаемого?
Нормативный метод чаще применяется для программных или целевых прогнозов. Используются как количественное выражение норматива, так и определенная шкала возможностей оценочной функции.
В случае использования количественного выражения, например физиологических и рациональных норм потребления отдельных продовольственных и непродовольственных товаров, разработанных специалистами для различных групп населения, можно определить уровень потребления этих товаров на годы, предшествующие достижению указанной нормы. Такие расчеты называют интерполяцией. Интерполяция — это способ вычисления показателей, недостающих в динамическом ряду явления, на основе установленной взаимосвязи. Принимая фактическое значение показателя и значение его нормативов за крайние члены динамического ряда, можно определить величины значений внутри этого ряда. Поэтому интерполяцию считают нормативным методом. Ранее приведенная формула (4), используемая в экстраполяции, может применяться в интерполяции, где уп будет характеризовать уже не фактические данные, а норматив показателя.
В случае использования в нормативном методе шкалы (поля, спектра) возможностей оценочной функции, т. е. функции распределения предпочтительности, указывают примерно следующую градацию: нежелательно — менее желательно — более желательно — наиболее желательно — оптимально (норматив).
Нормативный метод прогнозирования помогает выработать рекомендации по повышению уровня объективности, следовательно, эффективности решений.
Метод экспертных оценок используется преимущественно в долгосрочных прогнозах. Прогнозирование осуществляется на основе суждения эксперта (группы экспертов) относительно поставленной задачи. Экспертом выступает квалифицированный специалист по конкретной проблеме, который может сделать достоверный вывод об объекте прогнозирования. Метод экспертных оценок чаще используется в тех случаях, когда трудно количественно оценить прогнозный фон, и специалисты делают это на основе своего понимания вопроса. По существу мнение специалиста — это результат мысленного анализа и обобщения процессов, относящихся к прошлому, настоящему и будущему, на основании собственного опыта, квалификации и интуиции. Метод экспертных оценок имеет несколько видов: индивидуальная экспертная оценка; коллективная экспертная оценка; метод психоинтеллектуальной генерации идей; аналитический метод; метод интервью; метод экспертных комиссий; дельфийский метод; метод коллективной генерации идей; метод управляемой генерации идей; синоптический метод и др.
Метод аналогии предполагает перенос знаний об одном предмете (явлении) на другой. Такой перенос верен с определенной долей вероятности, так как сходство между явлениями редко бывает полным.
Различают аналогию историческую и математическую. Метод исторической аналогии основан на установлении и использовании аналогии объекта прогнозирования с одинаковыми по природе объектами, которые опережают прогнозируемые в своем развитии. Примером могут служить прогнозы экономического развития страны, переходящей в конце XX в. на рыночную модель экономики, построенные с учетом аналогии развития стран, имеющих длительную историю рыночных отношений. Метод математической аналогии основан на установлении аналогии математических описаний процессов развития различных по природе объектов с последующим использованием более изученного и более точного математического описания одного из них для разработки прогнозов другого. Этот метод используется в экономико-математическом моделировании и при экспериментальном подходе к изучению экономики, когда знание о признаках одного предмета возникает на основании его сходства с другими предметами. Например, после исследования определенной модели можно сделать вывод, хотя и не окончательный, о системе. Моделирование и эксперимент обязательно используют метод аналогии.
Моделирование, пожалуй, самый сложный метод прогнозирования. Математическое моделирование означает описание экономического явления посредством математических формул, уравнений и неравенств. Математической аппарат должен достаточно точно отражать прогнозный фон, хотя полностью отразить всю глубину и сложность прогнозируемого объекта довольно трудно. Термин "модель" образован от латинского слова modelus, что означает "мера". Поэтому моделирование правильнее было бы считать не методом прогнозирования, а методом изучения аналогичного явления на модели.
В широком смысле моделями называются заместители объекта исследования, находящиеся с ним в таком сходстве, которое позволяет получить новое знание об объекте. Модель следует рассматривать как математическое описание объекта. В этом случае модель определяется как явление (предмет, установка), которое находится в некотором соответствии с изучаемым объектом и может его замещать в процессе исследования, представляя информацию об объекте.
При более узком понимании модели она рассматривается как объект прогнозирования, ее исследование позволяет получить информацию о возможных состояниях объекта в будущем и путях достижения этих состояний. В этом случае целью прогнозной модели является получение информации не об объекте вообще, а только о его будущих состояниях. Тогда при построении модели бывает невозможно провести прямую проверку ее соответствия объекту, так как модель представляет собой только его будущее состояние, а сам объект в настоящее время может отсутствовать или иметь иное существование.
Модели могут быть материальными и идеальными.
В экономике используются идеальные модели. Наиболее совершенной идеальной моделью количественного описания социально-экономического (экономического) явления является математическая модель, использующая числа, формулы, уравнения, алгоритмы, или графическое представление.
С помощью экономических моделей определяют:
-
зависимость между различными экономическими показателями;
-
различного рода ограничения, накладываемые на показатели;
♦ критерии, позволяющие оптимизировать процесс.
Содержательное описание объекта может быть представлено в виде его формализованной схемы, которая указывает, какие параметры и исходную информацию нужно собрать, чтобы вычислить искомые величины. Математическая модель в отличие от формализованной схемы содержит конкретные числовые данные, характеризующие объект. Разработка математической модели во многом зависит от представления прогнозиста о сущности моделируемого процесса. На основе своих представлений он выдвигает рабочую гипотезу, с помощью которой создается аналитическая запись модели в виде формул, уравнений и неравенств. В результате решения системы уравнений получают конкретные параметры функции, которыми описывается изменение искомых переменных величин во времени.
В экономическом прогнозировании различают: макромоделирование, т. е. укрупненное моделирование показателей экономики страны в целом, и микромоделирование, т. е. построение моделей для отдельного объекта (фирмы).
Макромоделирование осуществляется в основном на уровне государства; проводить его могут различные учреждения, в том числе научные. Между уровнями макро- и микро- может находиться еще один уровень — мезоуровень, характеризующий моделирование экономических процессов региона, отрасли.
Из существующего множества моделей в экономике активно используются: прогностические, плановые и производственные модели.
Прогностические и плановые модели позволяют оптимизировать разрабатываемые экономические показатели для достижения выбранных целей деятельности. Эти модели призваны обеспечить количественную оценку различных вариантов экономического показателя в соответствии с заложенным в модель критерием оптимальности. Производственные модели предназначены для управления производством фирмы или отрасли, в том числе экономическими средствами.
Возможности использования экономико-математического моделирования весьма широки — от анализа до выработки управленческого решения, включая вопросы прогнозирования развития хозяйственных процессов. Однако нельзя переоценивать значение моделирования. Обычно моделирование рекомендуется использовать как "консультирующее средство", но окончательное решение всегда должно оставаться за специалистом. Это диктуется чрезвычайной сложностью живой социально-экономической среды. Указанная особенность приобретает важное значение в прогнозировании, когда прогноз используется в качестве основы для дальнейшего процесса — планирования.
При построении моделей соблюдаются определенные правила их испытания и проверки. При этом необходимо обнаружить и устранить недостатки, среди которых наиболее типичные:
-
включение в модель несущественных переменных величин;
-
невключение в модель существенных переменных величин;
-
недостаточно точная оценка параметров модели;
-
неправильное определение функциональной зависимости принятого критерия от управляемых и неуправляемых переменных.
Чтобы построить более точную и подробную модель, необходимо ее усложнить, что не всегда компенсируется возросшими трудностями расчетов. Существует и другая крайность: при упрощении модели возможно снижение ее достоверности. Эти два полюса должны учитываться прогнозистом при использовании метода моделирования.
Методы прогнозирования не исчерпываются указанными. В специальной литературе можно найти описание иных методов:
-
морфологический анализ;
-
прогнозный сценарий;
-
прогнозный граф и "дерево целей";
-
корреляционный и регрессионный анализ;
-
метод группового учета аргументов;
-
факторный анализ;
-
теория распознавания образов;
-
вариационные исчисления;
-
спектральный анализ и др.
Таким образом, существуют различные типовые методы прогнозирования. Задача прогнозиста — выбрать такой метод, который в наибольшей мере соответствовал бы задачам и принципам прогнозирования данного явления (объекта). При соответствии методов прогнозирования заданным принципам можно говорить о создании прогнозируемой системы объекта.
