
Вопросы для самоконтроля знаний
-
Как вводится система координат на прямой?
-
Как вводится прямоугольная система координат на плоскости?
-
Что называется координатами точки в прямоугольной системе координат на плоскости?
-
Как вводится прямоугольная система координат в пространстве?
-
Что называется координатами точки в прямоугольной системе координат в пространстве?
-
По какой формуле вычисляется расстояние между двумя точками на плоскости и в пространстве?
-
Какие величины называются скалярными, а какие
 векторными?
векторными? -
Что называется вектором?
-
Какие векторы называются коллинеарными?
-
Какие векторы называются равными?
-
Какие векторы называются противоположными?
-
Какие векторы называются компланарными?
-
Что называется проекцией вектора на ось?
-
Что называется координатами вектора?
-
Как определяются координаты вектора, если известны координаты точки его начала и точки его конца?
-
Если известны координаты вектора, то чему равна его длина?
-
Какие операции над векторами называются линейными?
-
Что является необходимым и достаточным условием коллинеарности двух векторов?
-
Как определяется скалярное произведение двух векторов?
-
Что является необходимым и достаточным условием ортогональности двух векторов?
Задания для самостоятельной работы
-
Даны векторы
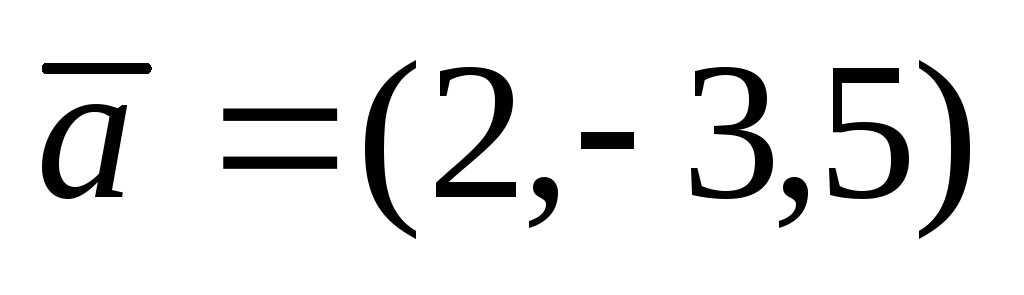 ,
,
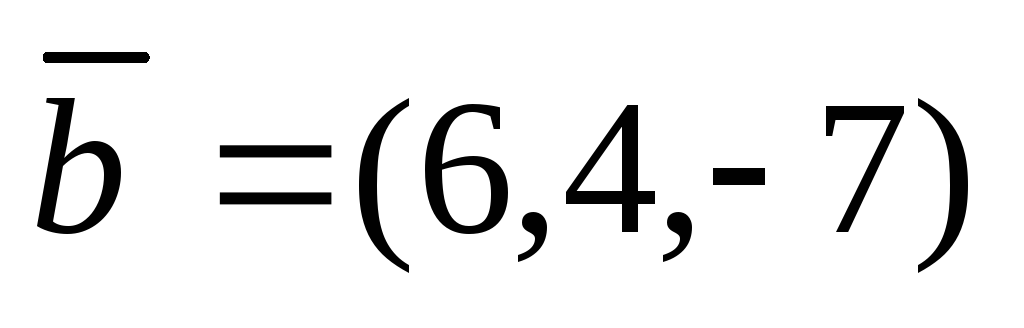 ,
,
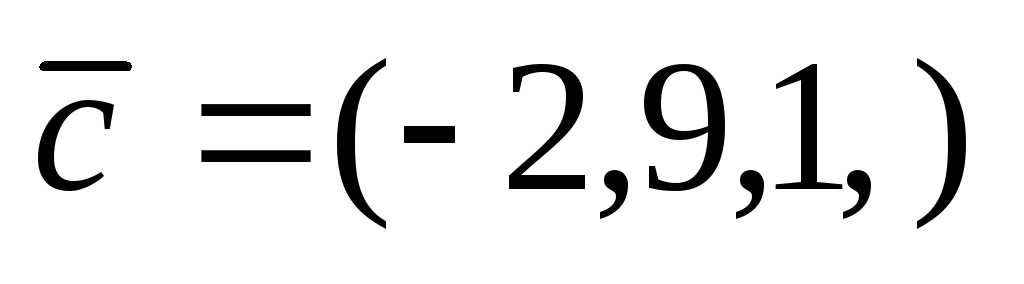 .
Найти векторы
.
Найти векторы
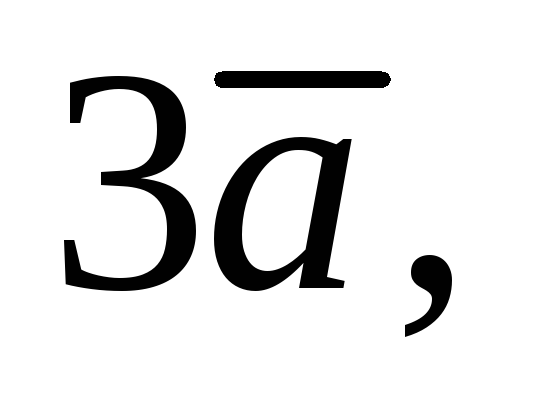
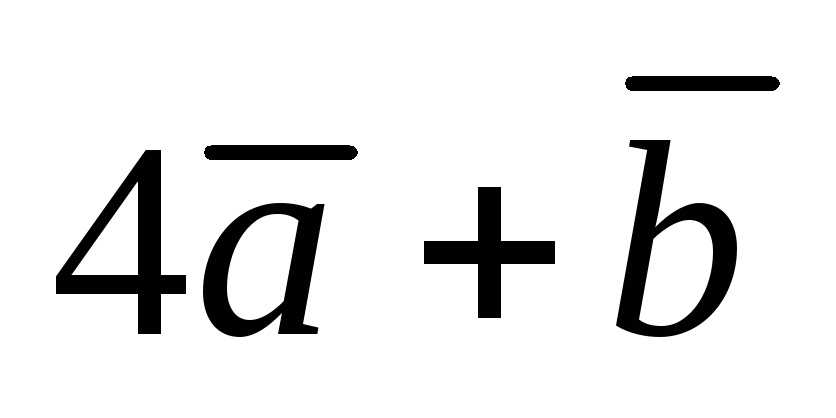 ,
,
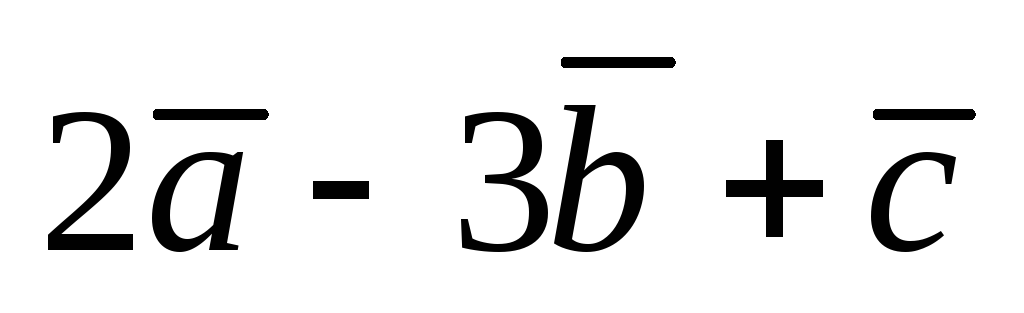 .
.
-
Даны векторы
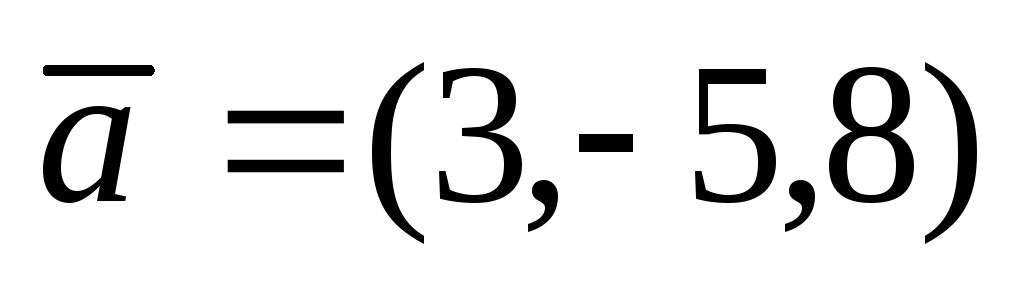 ,
,
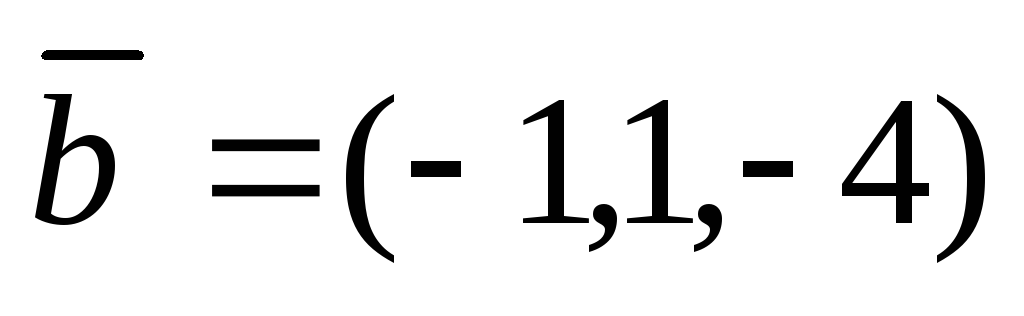 .
Найти длины векторов
.
Найти длины векторов
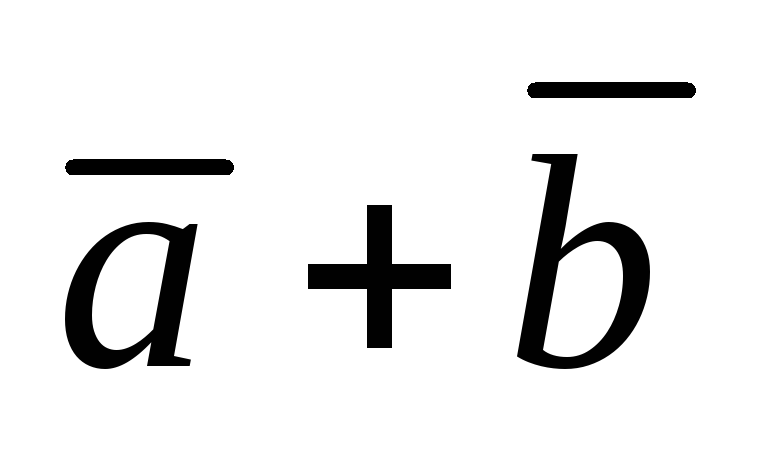 и
и
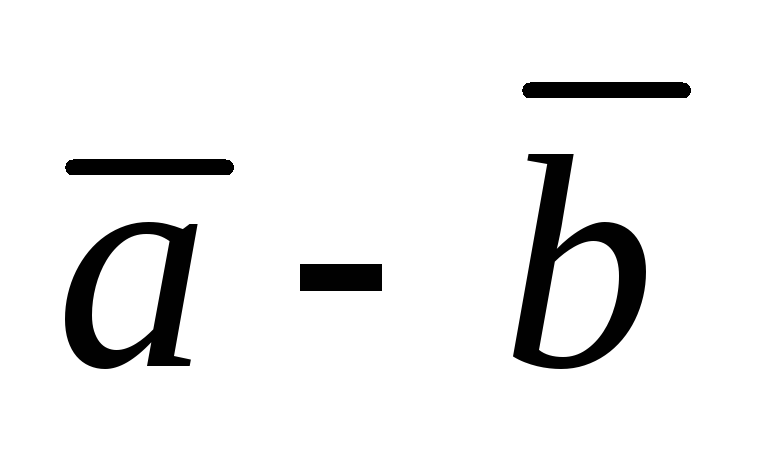 .
. -
Даны вершины треугольника
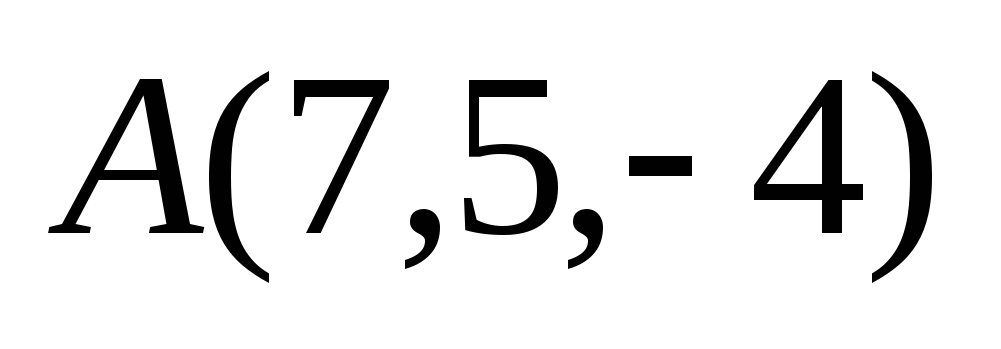 ,
,
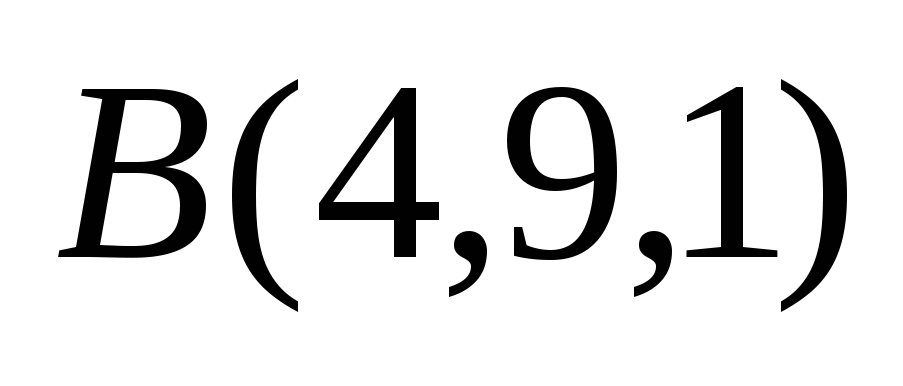 ,
,
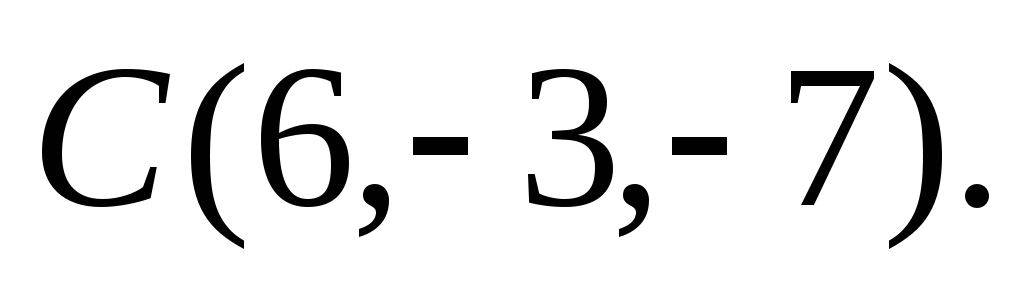 Найти длину медианы, проведённой из
вершины А,
и периметр треугольника.
Найти длину медианы, проведённой из
вершины А,
и периметр треугольника. -
Точки
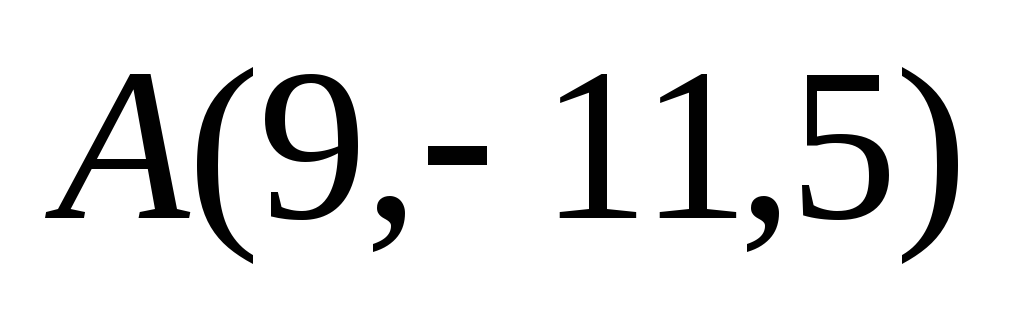 ,
,
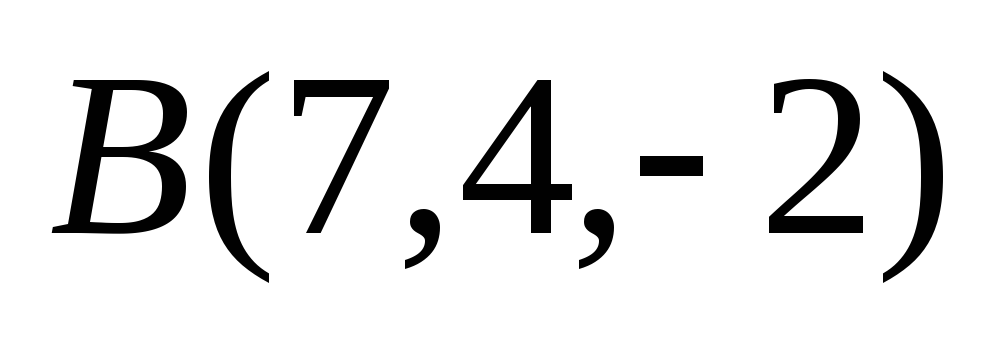 ,
,
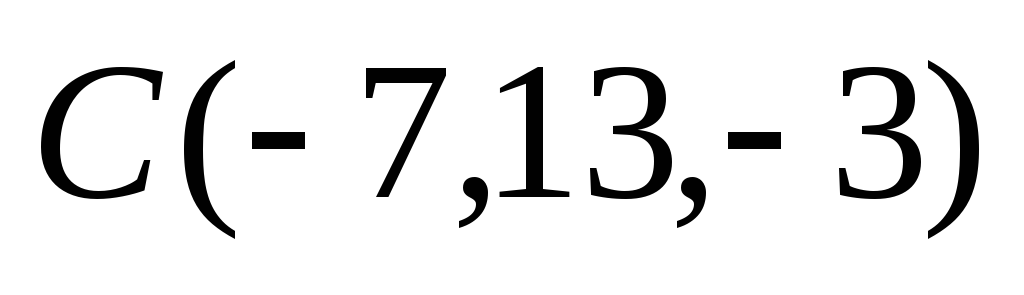 являются последовательными вершинами
ромба. Найти четвёртую вершину, вычислить
периметр ромба и длины его диагоналей.
являются последовательными вершинами
ромба. Найти четвёртую вершину, вычислить
периметр ромба и длины его диагоналей. -
Вычислить скалярное произведение векторов
 и
и
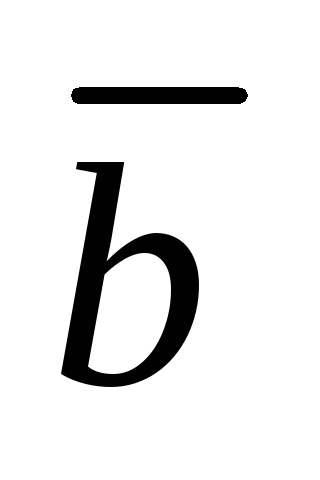 ,
если
,
если
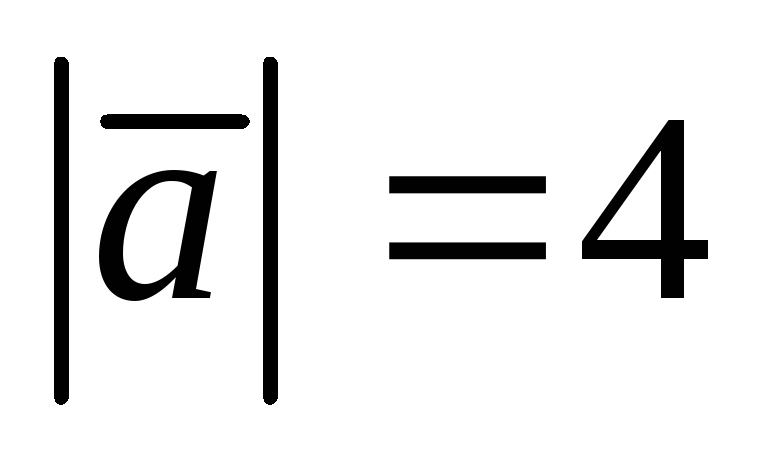 ,
,
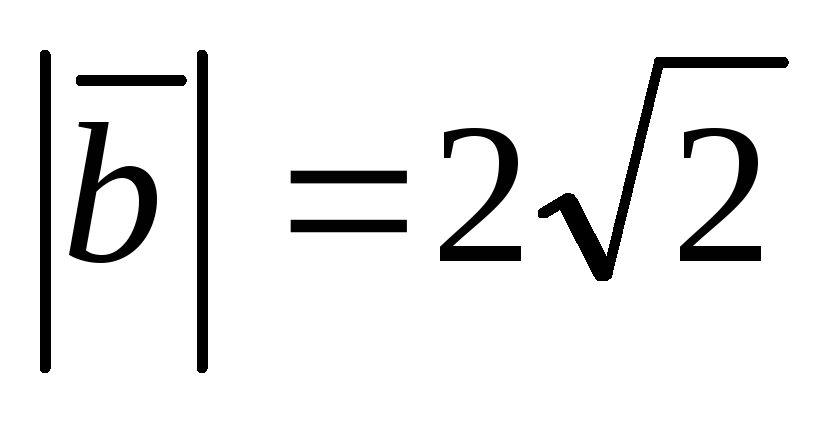 ,
,
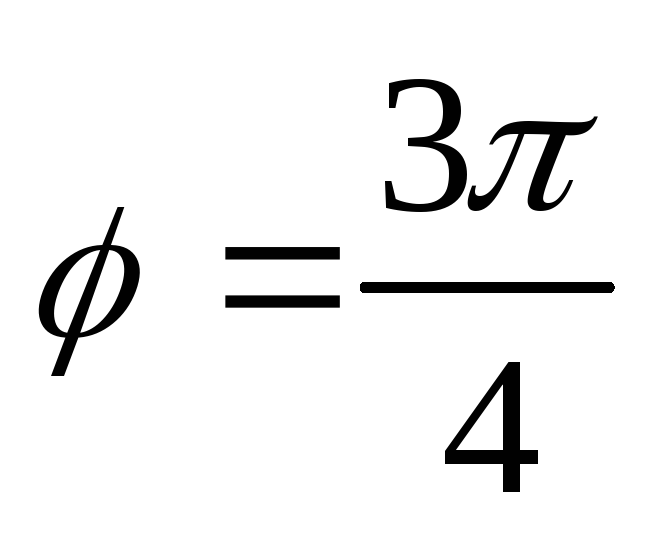 .
.
-
Вычислить скалярное произведение векторов
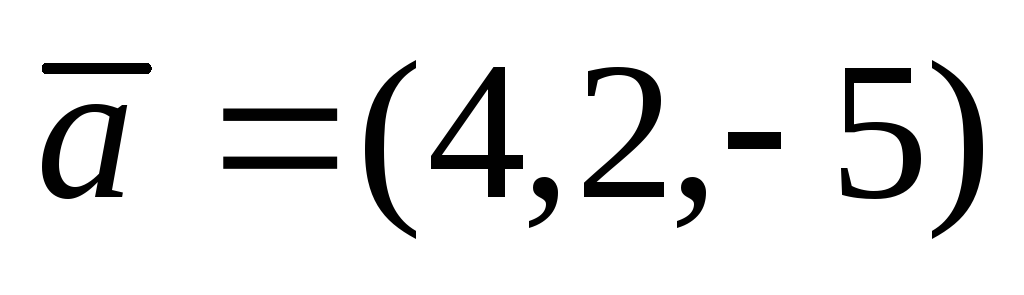 и
и
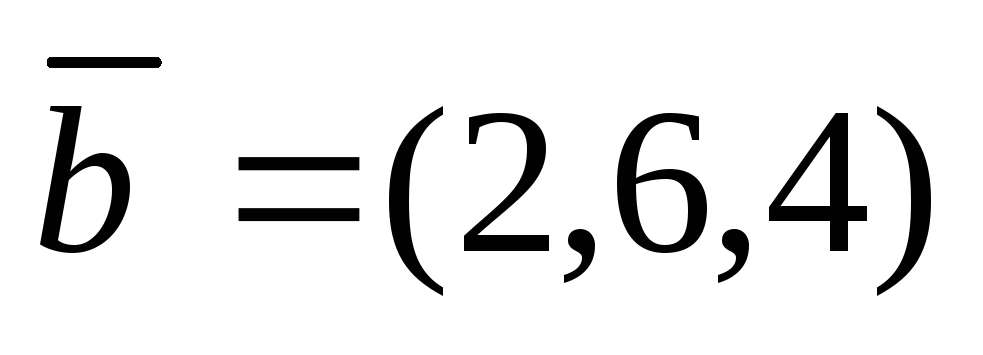 .
. -
Найти угол между векторами
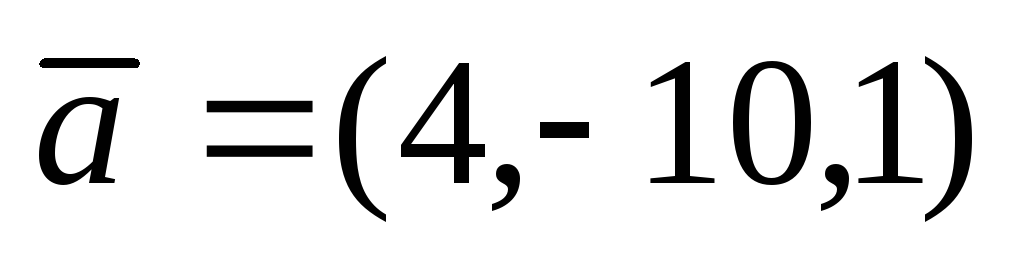 и
и
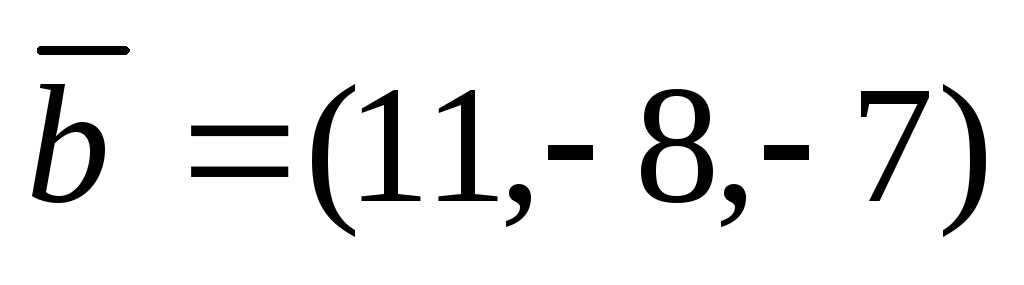 .
. -
Дан треугольник с вершинами
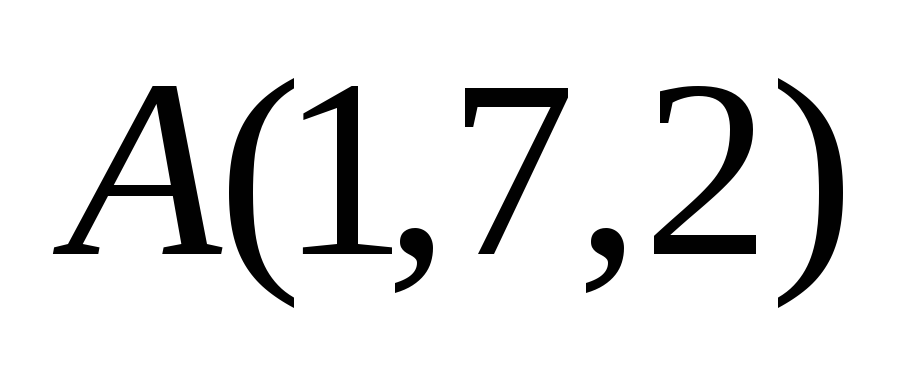 ,
,
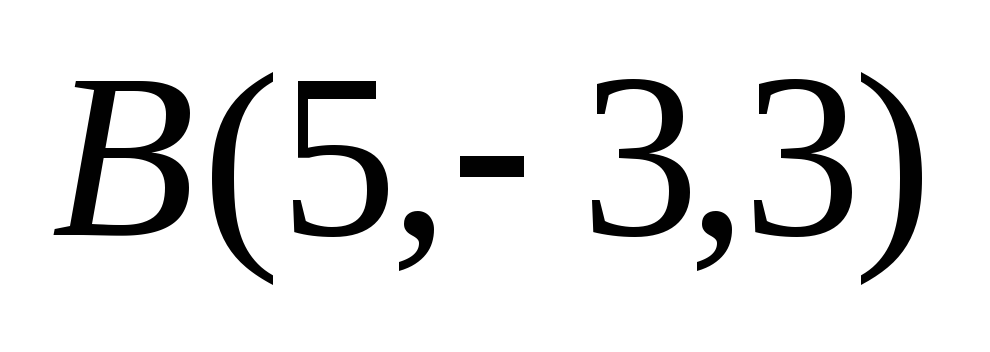 ,
,
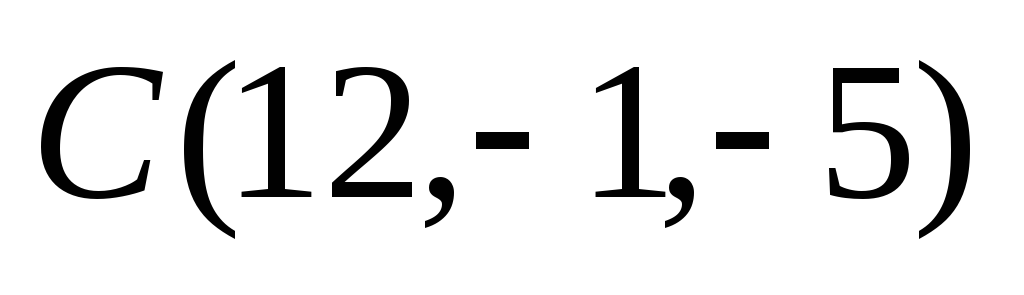 .
Найти внутренние углы этого треугольника.
.
Найти внутренние углы этого треугольника. -
Вычислить проекцию вектора
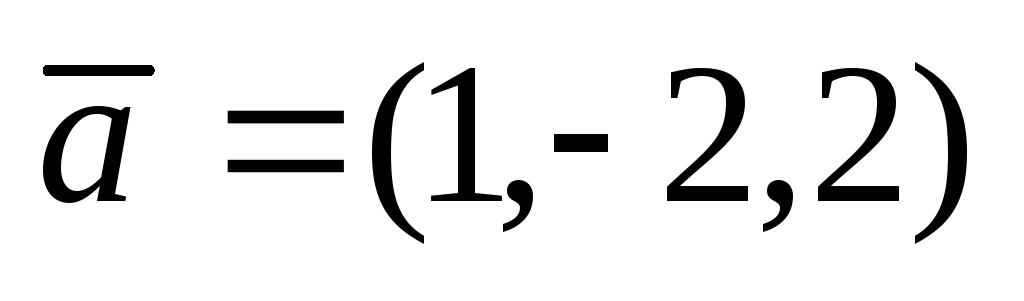 на вектор
на вектор
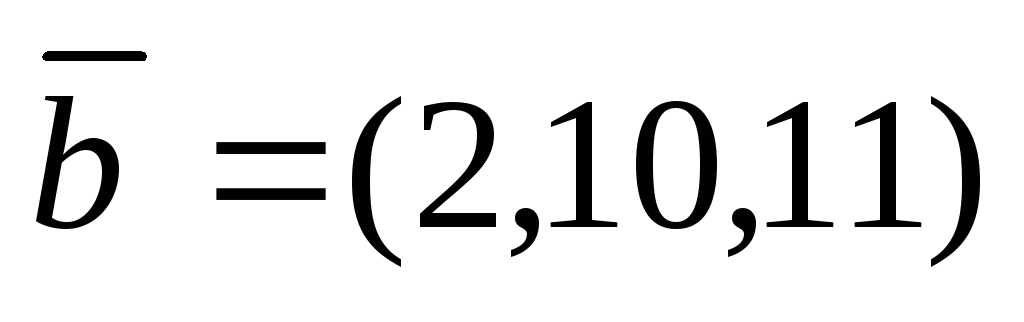 .
. -
Даны векторы
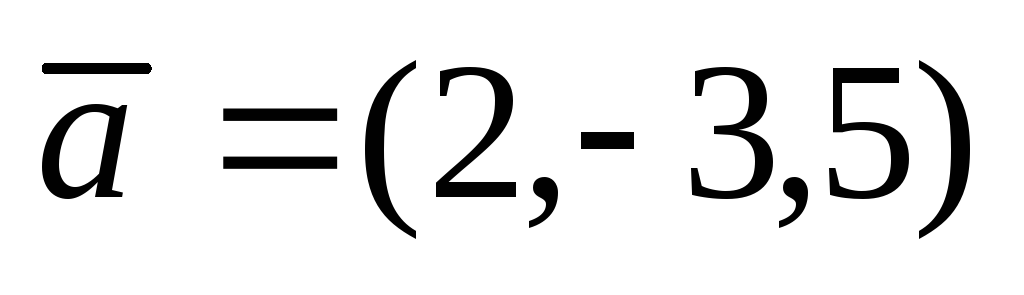 и
и
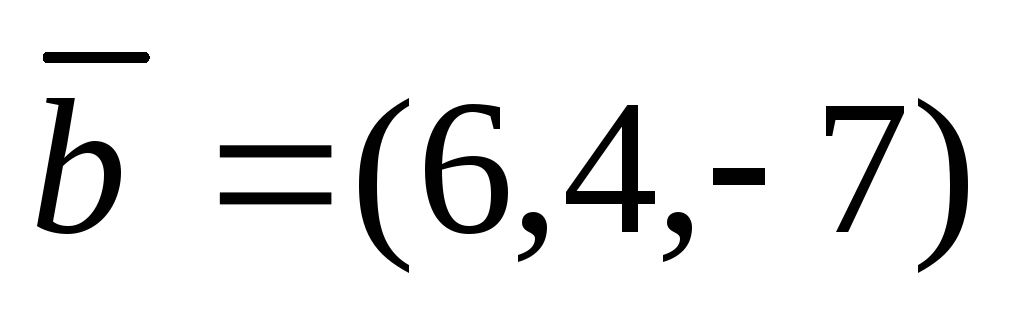 . Найти проекцию вектора
. Найти проекцию вектора
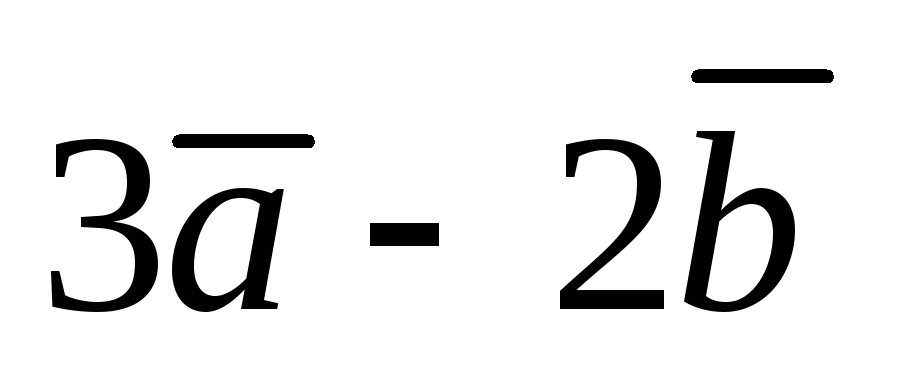 на вектор
на вектор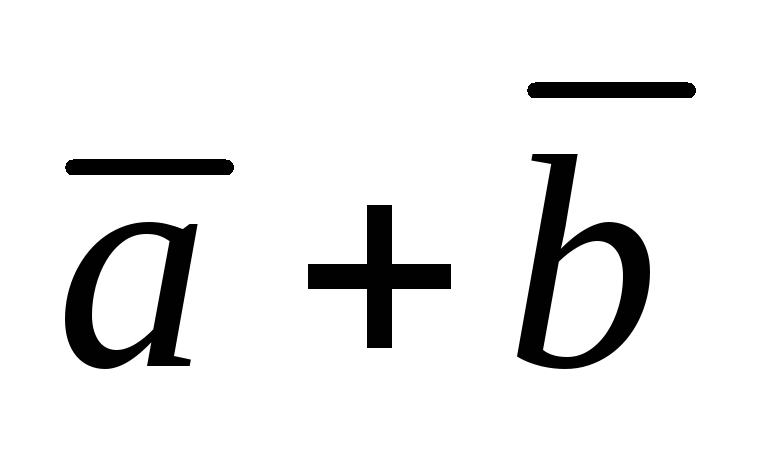 .
.
-
Найти угол между векторами
 ,
,
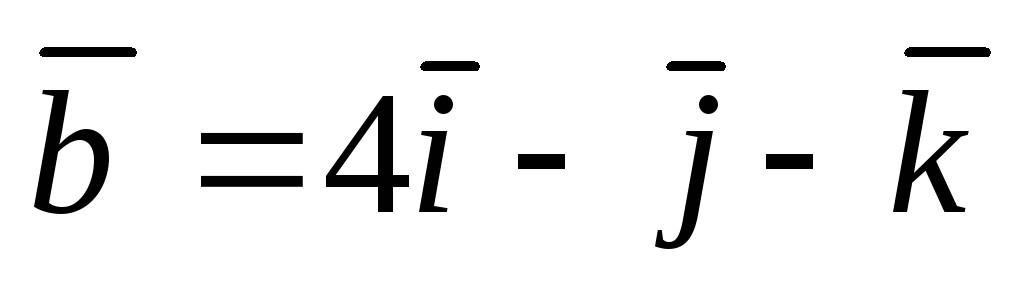 .
.
-
Найти, при каком значении m векторы
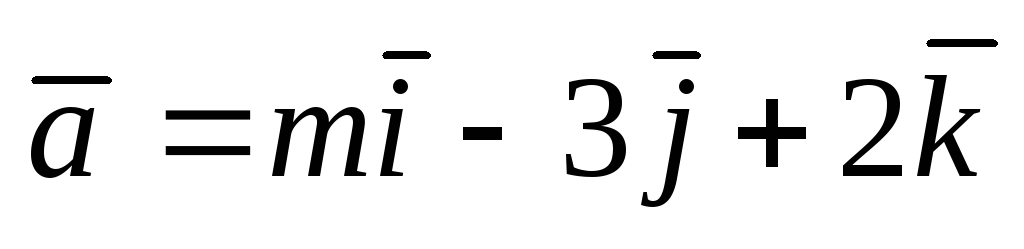 и
и
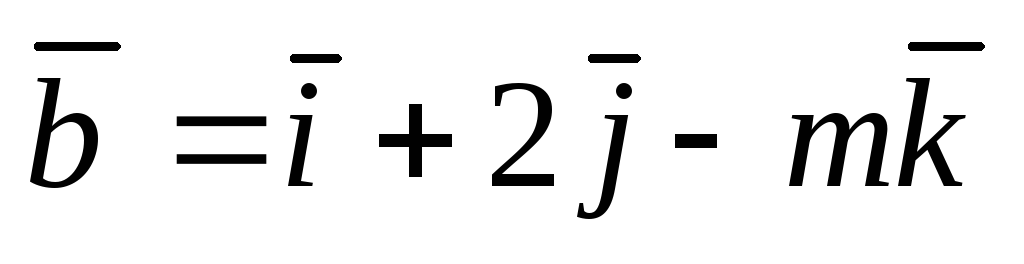 будут взаимно перпендикулярными.
будут взаимно перпендикулярными. -
Найти проекцию вектора
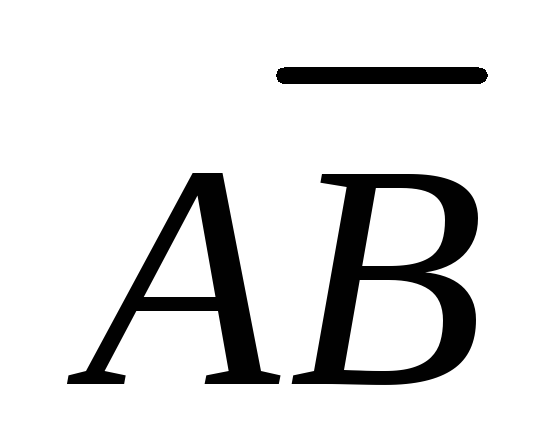 на вектор
на вектор
 ,
если известны точки
,
если известны точки
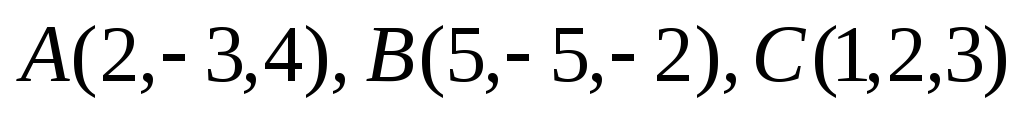 и
и
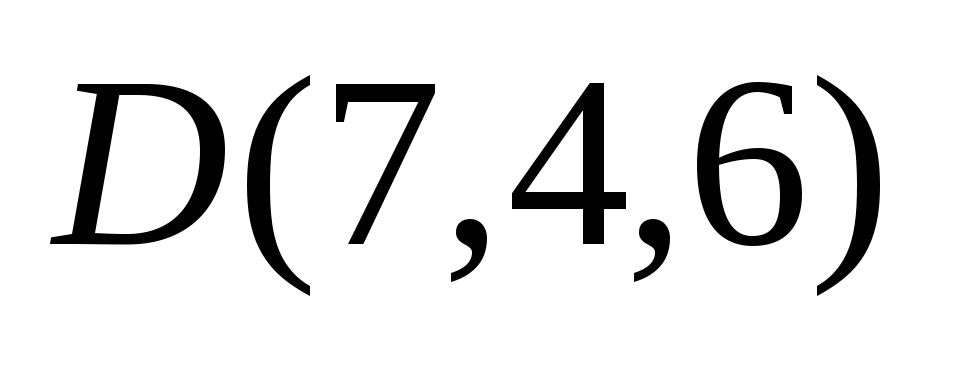 .
. -
Даны вершины четырёхугольника
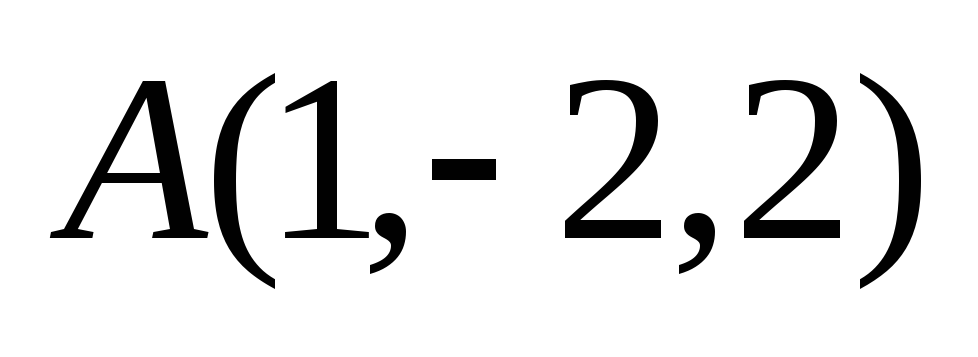 ,
,
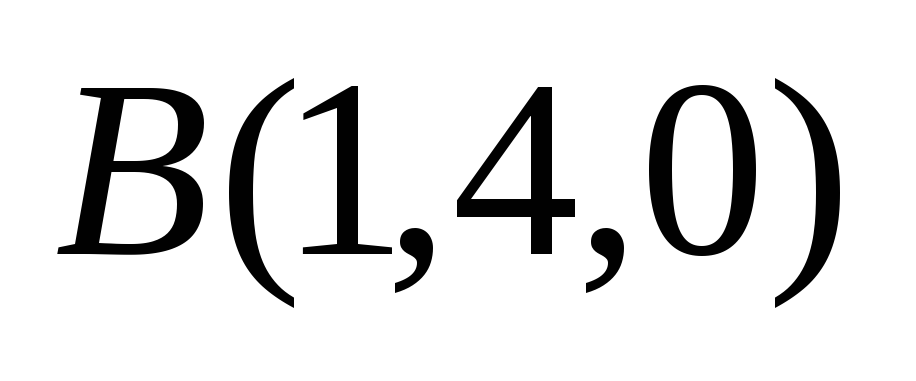 ,
,
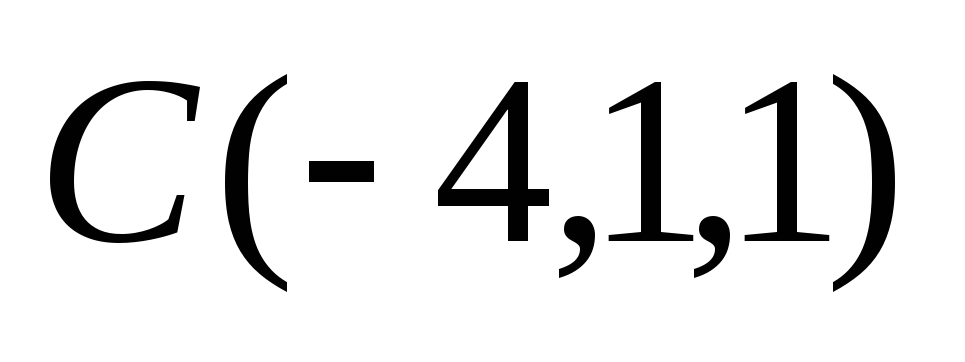 и
и
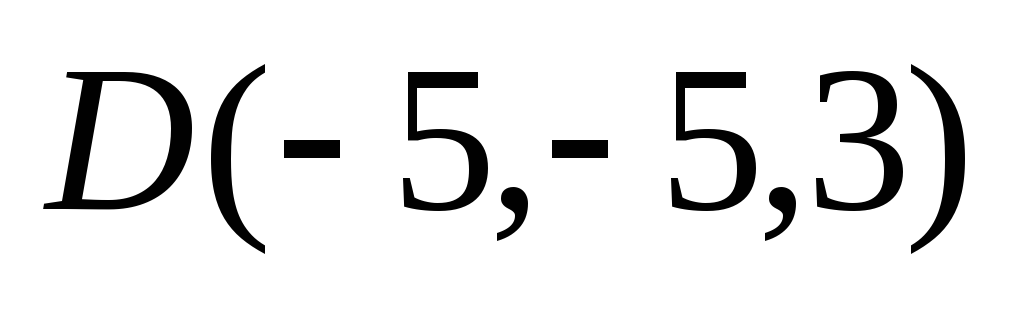 .
Вычислить угол между его диагоналями.
.
Вычислить угол между его диагоналями.
