4. Определённый интеграл и его основные свойства

Пусть функция определена на отрезке . Выполним следующие действия.

Разобьём отрезок точками … , на n отрезков , , … , , которые называются частичными.

В каждом частичном отрезке произвольно выберем точку , вычислим значение функции в этой точке и произведение , где .

Если существует предел , который не зависит ни от способа разбиения отрезка , ни от выбора точек , то он называется определённым интегралом от функции на отрезке и обозначается

.

Числа a и b называются нижним и верхним пределами интегрирования. Функция называется подынтегральной функцией, выражение - подынтегральным выражением, x – переменной интегрирования, - отрезком интегрирования.

Пусть на отрезке задана непрерывная функция . Фигура, ограниченная сверху графиком функции , снизу осью Ox, сбоку – прямыми x=a и x=b, называется криволинейной трапецией.

Определённый интеграл от неотрицательной функции численно равен площади криволинейной трапеции. В этом состоит геометрический смысл определённого интеграла.

Основными свойствами определённого интеграла являются следующие:

постоянный множитель можно выносить за знак определённого интеграла, т.е. ;

определённый интеграл от алгебраической суммы непрерывных на отрезке функций и равен алгебраической сумме определённых интегралов от этих функций, т.е.

;

если верхний и нижний пределы интегрирования поменять местами, то определённый интеграл изменит знак на противоположный, т.е. ;

если пределы интегрирования равны между собой, то определённый интеграл равен нулю, т.е. ;

определённый интеграл не зависит от обозначения переменной интегрирования, т.е. …;

если отрезок интегрирования разбит на две части и и если существуют интегралы и , то

.

Для вычисления определённых интегралов используется формула Ньютона-Лейбница

,

где , т.е. - любая первообразная функция для .

5. Методы вычисления определённых интегралов

При вычислении определённых интегралов используются методы непосредственного интегрирования, замены переменной (подста-

новки) и интегрирования по частям.

Непосредственное интегрирование предполагает сведение данного интеграла с помощью алгебраических и арифметических преобразований к формулам таблицы основных интегралов и использование формулы Ньютона-Лейбница.

Примеры 10-11. Вычислить интегралы: а) ; б) .

Решение. а) =;

б) =.

Метод замены переменной в определённом интеграле предполагает следующее. Пусть выполнены условия:

функция непрерывна на отрезке ;

функция определена на отрезке и имеет на нём непрерывную производную;

, .

Тогда определённый интеграл может быть вычислен с помощью введения новой переменной и при этом справедлива формула . Часто вместо замены применяют обратную замену .

Примеры 12–13. Вычислить интегралы: а); б).

Решение. а) Выполним замену , . Вычислим пределы интегрирования для переменной t:

x	0	1
t	1	2

Тогда =.

б) Выполним замену и продифференцируем обе части равенства: , . Изменим пределы интегрирования:

x	-2	0
t	9	1

В результате =

.

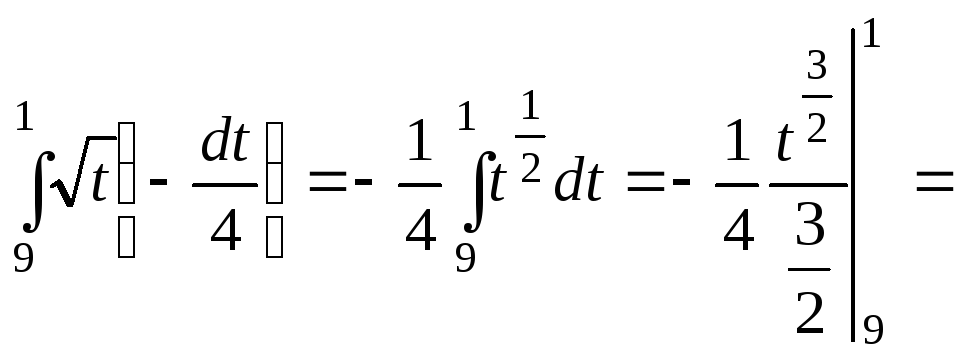
Пусть функции и имеют непрерывные производные на отрезке . Тогда для определённого интеграла справедлива формула интегрирования по частям .

Пример 14. Вычислить интеграл .

Решение. Положим u=x, тогда du=dx. Оставшуюся часть подынтегрального выражения примем за dv: . Проинтегрируем это выражение: , . Тогда по формуле интегрирования по частям получим ==