Апроксимація емпіричних даних методом найменших квадратів

Необхідність розв’язання несумісних систем досить часто виникає у практичних розрахунках, наприклад при аналізі емпіричних даних, у тому числі й економічних. В економіці розглядаються зв'язки між вартістю продукції, обсягом виробництва, ціною й прибутком. Незважаючи на складність цих зв'язків, у певних моделях вони можуть бути лінійними. Нехай, наприклад, випуск екземплярів виробу обходиться у суму , випуск екземплярів виробу обходиться у суму і т.д. Тоді виробник може оцінити суму витрат у на наступному тижні, припустивши, що вона лінійно залежить від обсягу випуску t, і оцінивши значення коефіцієнтів с, d по вже наявним даним. Коефіцієнт с називається граничною вартістю виробництва, а коефіцієнт d визначає накладні витрати. Припустивши, що емпіричні дані підкоряються залежності , одержимо відносно невідомих с, d систему лінійних алгебраїчних рівнянь

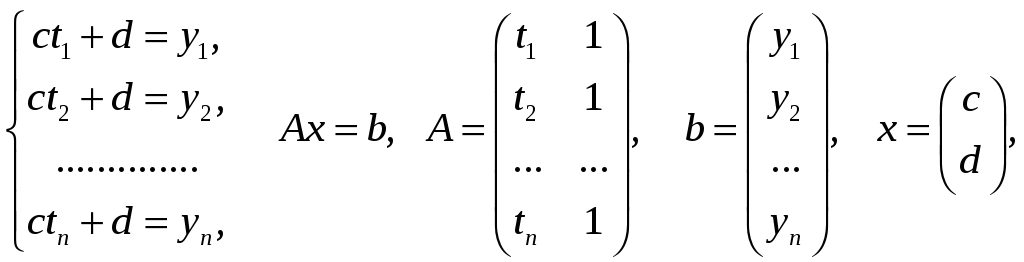
у якій при n > 2 рівнянь більше, ніж невідомих. Лінійна система, число рівнянь у якій більше числа невідомих, називається перевизначеною.

Якщо лінійне співвідношення дійсно справедливо й емпіричні дані виміряні точно, то отримана система сумісна, ранг матриці дорівнює двом (кількість невідомих) і значення коефіцієнтів лінійної залежності можна знайти з перших двох рівнянь системи. На практиці така ситуація неможлива - емпіричні дані за своєю природою завжди містять помилку, а лінійна модель лише приблизно описує реальні зв'язки величин. Отже, система несумісна і її нормальний узагальнений розв’язок дозволяє знайти найкращі наближені значення коефіцієнтів лінійної функції, оскільки в цьому випадку нев'язка мінімальна. Побудованому в такий спосіб розв’язку можна дати геометричну інтерпретацію. Оскільки 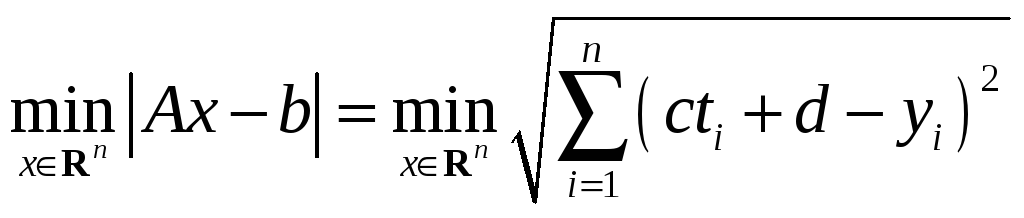, то лінійна залежність - це пряма на площині змінних , сума квадратів відстаней до якої від заданих емпіричних точок мінімальна. Нормальний узагальнений розв’язок в цьому випадку є розв’язанням нормальної системи методу найменших квадратів:

де

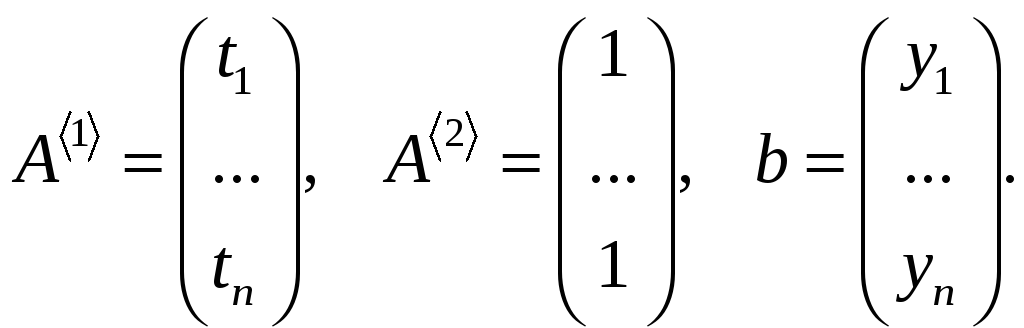
Приклад. Для вивчення залежності октанового числа бензину від чистоти каталізатора (%) провели 11 вимірів, наведених нижче.

Таб.1.

Октанове число	98.8	98.9	99.0	99.1	99.2	99.3	99.4	99.5	99.6	99.7	99.8
Чистота каталізатора	87.1	86.6	86.4	87.3	86.1	86.8	87.2	88.4	87.2	86.4	88.6

Треба знайти коефіцієнти a, b лінійної залежності y = ах + b октанового числа від чистоти каталізатора та обчислити значення октанового числа, якщо чистота каталізатора складає 87%. Фрагмент робочого листа MathCad з відповідними розрахунками наведено на рис.1.

Рис.1.

Вказівка. Щоб уникнути ручного набору даних таблиця 1 була скопійована і збережена у файлі Excel. Потім за допомогою команди і далі в режимі діалогу збережена як масив Z. Функції іntersept(x, у) і slope(x, у) повертають значення коефіцієнтів a і b лінійної функції y = ах + b, що апроксимує експериментальні дані, збережені у векторах X і Y. Значення октанового числа, обчислені для частоти каталізатора 0.870 по обох формулах, збігаються. Співпадають і наведені в останніх рядках робочого документа коефіцієнти лінійної функції, обчислені обома способами. На рис. 2 представлені відповідні графіки.

Рис.2.