Приклад розрахунку два рази статично невизначуваної плоскої рами методом сил

Необхідно: побудувати епюри згинальних моментів М, поперечних Q та поздовжніх N сил від заданого навантаження, а також підібрати поперечні перерізи і перевірити раму на міцність.

а) б)

Рисунок 1.2 – а) Задана схема статично невизначуваної рами та

Б) основна система.

1. Ступінь статичної невизначуваності . Тобто рама два рази статично невизначувана.

2. Система канонічних рівнянь буде мати вигляд:

3. Вибираємо основну систему методу сил, для чого відкидаємо „зайві” зв’язки у вигляді опорних реакцій опори (рис.1.2б).

4. Будуємо вантажну епюру для вантажного стану основної системи. Від одиничної силибудуємо одиничну епюрувід–.

а) б)

в) г)

Рисунок 1.3 – а) вантажний стан основної системи;

Б) вантажна епюра ; в) одиничний стан №1 та г) одинична епюра .

а) б)

Рисунок 1.4 – а) одиничний стан №2 та б) одинична епюра .

5. Підраховуємо одиничні та вантажні коефіцієнти. При підрахунках використовуємо залежність(береться з завдання), тобто. В подальшому приймемо скорочення.

За формулою Сімпсона-Корноухова:

За формулою Верещагіна:

За формулою Сімпсона-Корноухова:

За формулою Верещагіна:

6. Виконуємо перевірку знайдених коефіцієнтів системи канонічних рівнянь.

а) построкову:

;

;

.

Рисунок 1.5 – Сумарна

одинична епюра

;

;

.

б) універсальну

.

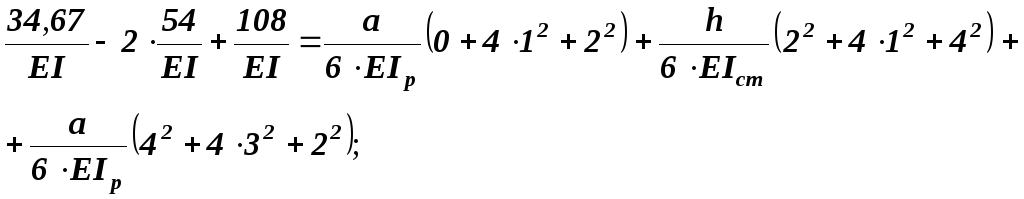
в) постовпчикову

7. Підставляємо підраховані коефіцієнти в систему канонічних рівнянь і розв’язуємо відносно невідомих та. Отже, маємо:

.

Рисунок 1.6 – Одиничні виправлені епюри

8. Будуємо виправлені епюри, помножаючи ординати одиничних епюр на відповідні значення невідомих (епюру на, а епюруна) – див. рис. 1.6, а також сумарну виправлену епюру(шляхом складання епюрта) – див. рис. 1.7.

Рисунок1.7 – Сумарна виправлена

одинична епюра

9. Будуємо остаточну розрахункову

епюру згинаючих моментів

шляхом складання вантажної

з сумарною виправленою

епюрами . Див. рис. 1.8.

Рисунок 1.8 – Остаточна епюра

Згинаючих моментів

1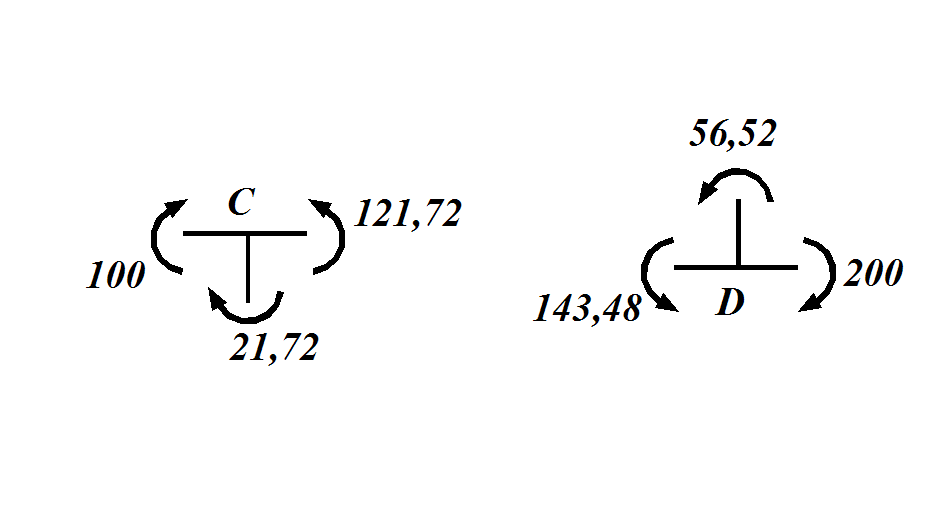0. Виконуємо перевірку правильності побудови епюри

а) статичну шляхом вирізання вузлів С та D.

б) кінематичну

Невелика похибка з’являється в результаті заокруглень при обчисленні.

11. За остаточною епюрою моментівбудуємо епюру поперечних сил, використовуючи формулу Журавського. А за епюрою поперечних сил будуємо епюру поздовжніх зусиль.

Слід зазначити, що будувати епюри ,таможна приклавши до основної системи зовнішнє навантаження та отримані в результаті розв’язку системи канонічних рівнянь значень невідомихта. Остаточні епюритапоказані на рис.1.10.

Ділянка ЕС:кН;

Ділянка ВД: кН;

Ділянка СА:кН.

Ділянка СD:кН;

Ділянка DK: кН: .

Рисунок 1.9 – Балочні епюри для ділянок СК та ЕD.

Рисунок 1.10 – Остаточні епюри та.

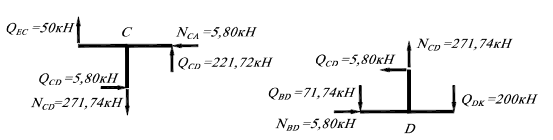
12. Перевіряємо правильність побудови епюр ташляхом розглядання рівноваги вузлів.

Вузол С:

Вузол D:

13. Підбираємо поперечні перерізи рами у вигляді двотавра.

Стрижень ЕА (ригель): ;

Стрижень BK (ригель): ;

Стрижень CD (стійка): .

За сортаментом підбираємо двотаври:

Стрижень ЕА (ригель): двотавр №55 (,)

Стрижень BK (ригель): двотавр №45 (,)

Стрижень CD (стійка): двотавр №27 (,)

або з метою зменшення кількості типорозмірів два двотаври № 45 ().

Визначивши розміри, перевіряємо міцність стрижнів:

Стрижень ЕА (ригель):;

Стрижень BK (ригель): ;

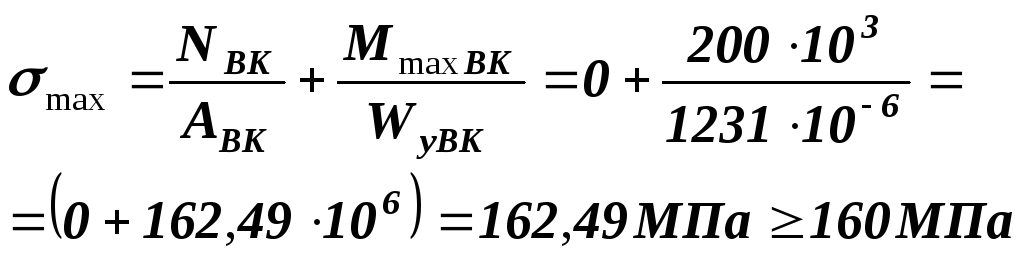Проте перенапруження складає 1,6 %.

Стрижень CD (стійка):

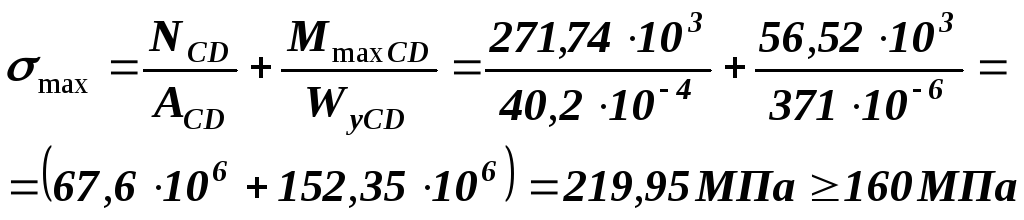
Оскільки умова міцності для стрижня CD не виконується, потрібно підібрати інший переріз. Приймаємо двотавр № 33 (,). Виконаємо перевірку:

Отже, остаточно підібрані такі перерізи: стрижень BK (ригель):

двотавр № 45; стрижень CD (стійка): двотавр № 33;

стрижень ЕА (ригель): двотавр № 55.