
ПРАКТИЧЕСКИЕ РАБОТЫ-12,13
.pdf
ПРАКТИЧЕСКИЕ РАБОТЫ № 12, 13
ТЕМА: Статистический анализ медико-биологических данных
Цель: Сформировать навыки статистической обработки медико-биологических данных. Выработать умение оценивать характеристики выборок, извлеченных из генеральных совокупностей различных распределений. Обеспечить профессиональную компетентность в плане проверки статистических гипотез и статистического обоснования полученных выводов.
План
1.Входной контроль.
2.Методы описательной статистики.
3.Исследование корреляционных связей. Графическая интерпретация.
4.Параметрические и непараметрические методы двухвыборочных сравнений.
ПОРЯДОК РАБОТЫ
Запустите LibreOffice Calc. Откройте файл статистика.ods и сохраните его под своим именем.
Использование статистических функций
Задание 1. Описательные статистики и гистограммы распределения.
Вычислите описательные статистики для переменных «индекс_1-6», используя встроенные статистические функции LibreOffice Calc. Известно, что выборочные распределения для всех переменных, кроме переменной «индекс_2», подчиняются нормальному закону распределения.
1. Для переменных, имеющих нормальный закон распределения, вычислите оценки среднего x
(статистическая функция – AVERAGE); дисперсии S2 (VAR); среднеквадратического отклонения
S (STDEV); стандартной ошибки среднего m Sn , где n = 30 – объем выборки; минимальное
значение (MIN) и максимальное значение (MAX) выборки; размах – разность между максимальным и минимальным значениями выборки.
2.Для переменных, закон распределения которых не соответствует нормальному, вычислите
медиану (MEDIAN); моду (MODA); нижний и верхний квартили (QUARTILE); минимальное значение (MIN) и максимальное значение (MAX) выборки; размах – разность между максимальным и минимальным значениями выборки.
3.Для переменной «индекс_2» вычислите оценку среднего, а для переменной «индекс_1» медиану и моду. Сравните между собой значения оценки среднего, медианы и моды для каждой переменной («индекс_1» и «индекс_2»). Объясните причину наблюдаемых различий.
4.Построить гистограммы частот для переменных «индекс_1» и «индекс_2». Сначала в ячейках L2:L7 посчитайте частоты для переменной «индекс_1». Для этого поставьте курсор мыши в ячейку L2 и с помощью мастера функций вызовите функцию ЧАСТОТА (FREQUENCY). В открывшемся
окне мастера функций в область дані введите диапазон данных переменной «индекс_1», а в область
класи – диапазон интервалов, на которые разбита переменная «индекс_1», т.е. выделите все значения в столбце «индекс_1 (масив интервалов)». Нажмите Гаразд.
1
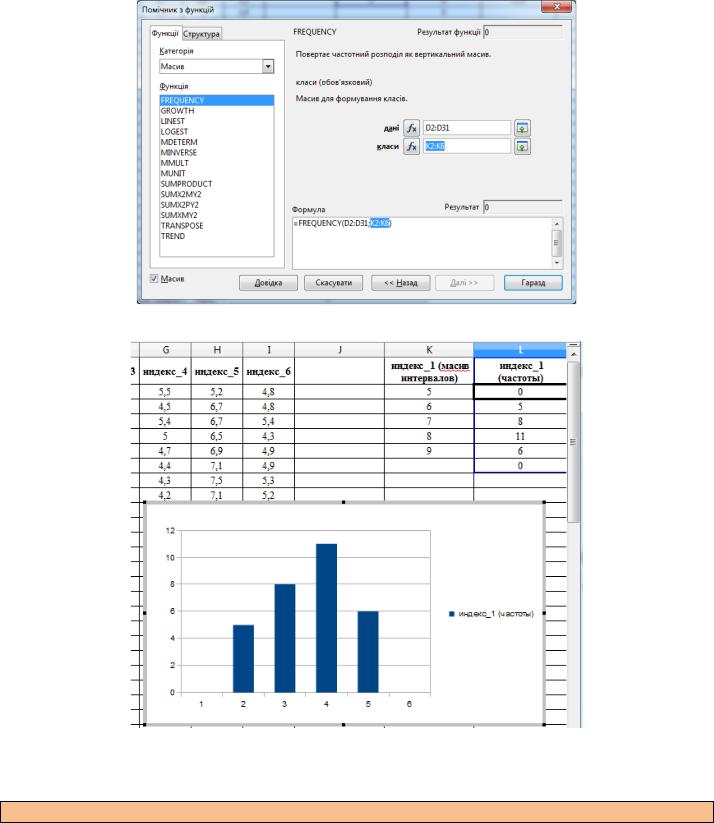
Результат вычисления частот появится в столбце L2:L6. По полученным данным постройте гистограмму. Должно быть так как показано на рисунке ниже.
Действуя аналогично, постройте гистограмму частот для переменной «индекс_2».
Посчитать характеристики для всех индексов. Построить гистограммы для всех индексов.
2

Как построить массив интервалов для гистограммы и саму гистограмму?
Рассмотрим процесс построения гистограммы «от А до Я» на примере переменной «индекс_3».
1.Необходимо разбить диапазон значений переменной на определѐнное количество интервалов равной длины.
1.1. Сначала определяем необходимое количество интервалов.
Теоретические сведения.
Количество интервалов, на которые надо разбивать диапазон значений переменной, может выбираться, исходя из различных предположений. Наиболее распространѐнный способ – использовать формулу Стерджесса, по которой количество интервалов разбиения:
k log2 N 1 3,322 lg N 1,
где N – количество наблюдений.
Ещѐ один из самых простых подходов – определить количество интервалов по
|
|
|
|
формуле: |
k N . |
||
Воспользуемся последней формулой ( k 
 N ). Т.к. в нашем случае количество наблюдений N = 30, то получаем k
N ). Т.к. в нашем случае количество наблюдений N = 30, то получаем k 
 30 5,48 :
30 5,48 :
Округляя полученное значение до ближайшего целого (используйте функцию ROUND, см. рис. на следующей странице), получаем, что необходимое количество интервалов k = 5:
3
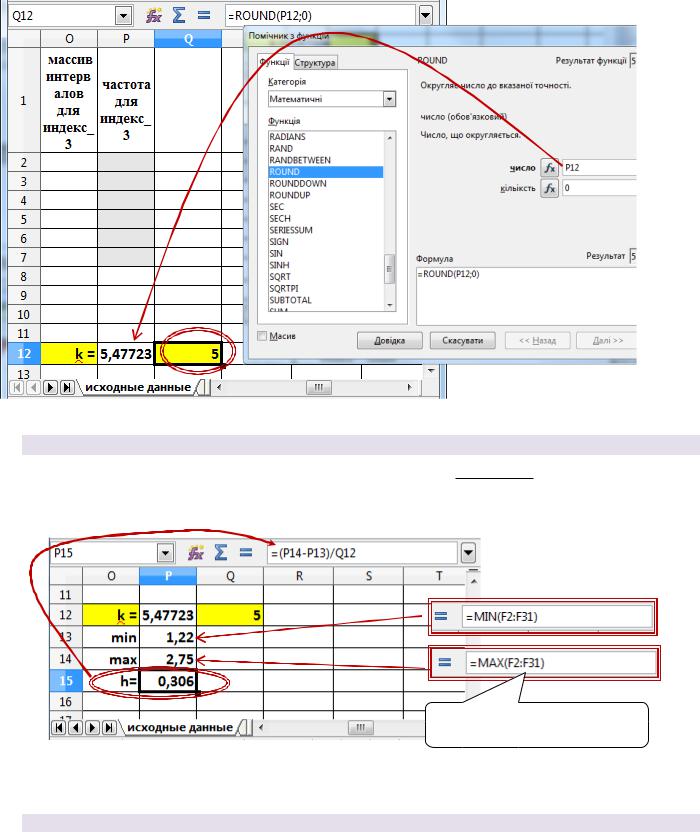
1.2. Находим длину интервалов.
Длина каждого интервала h определяется по формуле: h max min : k
F2:F31 – это диапазон значений переменной «индекс_3»
1.3. Определяем границы интервалов.
Верхняя граница первого интервала – это минимальное значение выборки + длина интервала
(min + h):
(см. рис. на следующей странице)
4
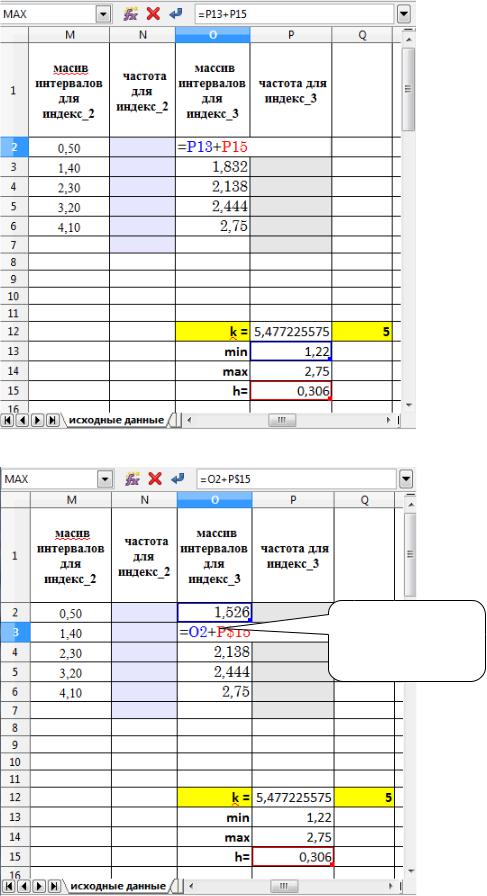
Верхняя граница каждого последующего интервала – это граница предыдущего интервала + h:
Формулу скопируйте протяжкой на оставшиеся три ячейки
Проверьте (!) – в качестве верхней границы последнего из интервалов разбиения должно получиться максимальное значение выборки.
5
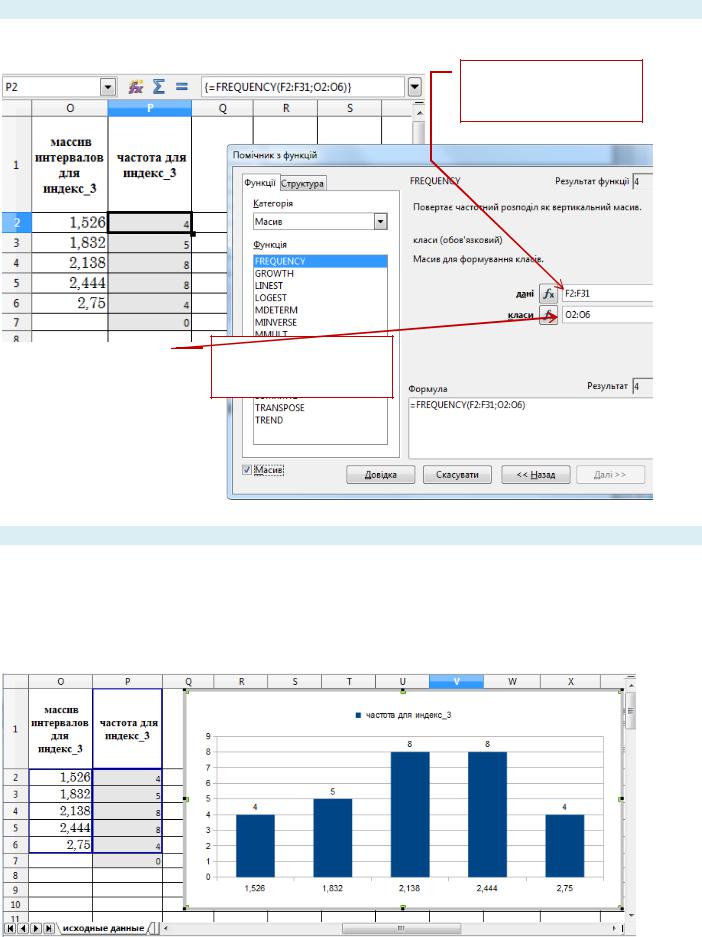
2. Подсчитать количество значений выборки, попадающий в каждый интервал.
Используйте функцию FREQUENCY:
Данные – это диапазон значений переменной «индекс_3»
Классы – это массив интервалов для переменной «индекс_3»
3. Построить гистограмму распределения переменной.
Для этого выделите диапазон частот переменной «индекс_3» и воспользуйтесь командой меню Вставка / Объект / Диаграмма… На третьем шаге работы мастера диаграмм (в окне «Ряды данных») в качестве категорий (т.е. подписей по оси Х) выделите диапазон значений массива верхних границ интервалов.
Если всѐ выполнено верно, получится гистограмма как на рисунке:
6
Задание 2. Корреляции.
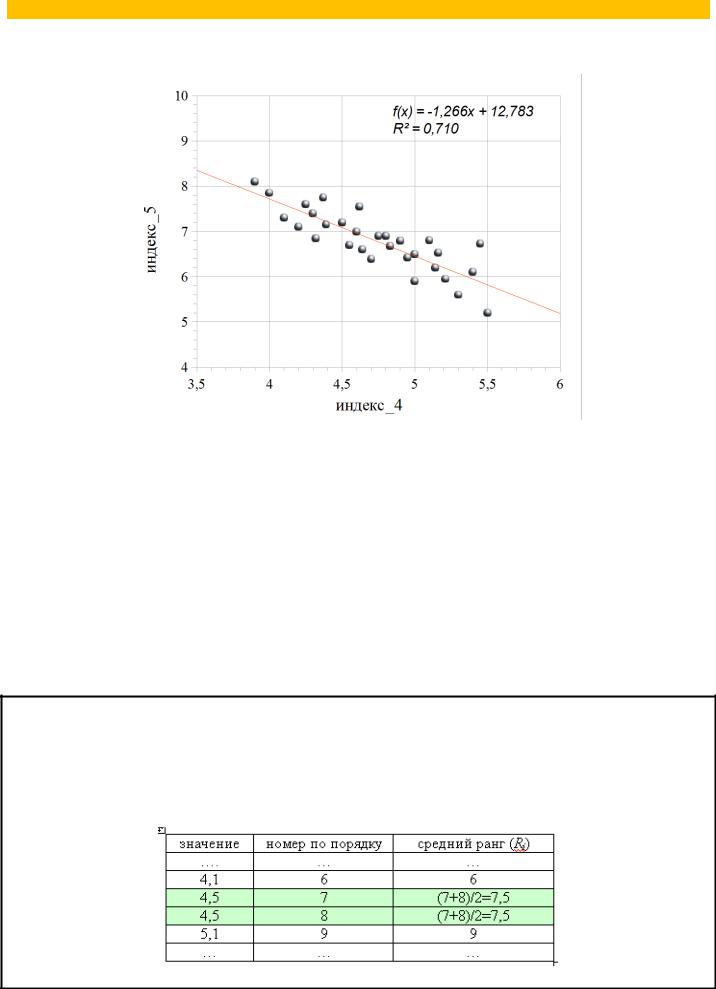
1. Перейдите на лист «корреляция». Постройте график рассеяния для переменных «индекс_4» и «индекс_5». На графике отобразите линейный тренд с указанием уравнения аппроксимации и значения R2. Параметры графика должны соответствовать образцу, приведенному ниже:
2.Для оценки силы связи между двумя переменными, имеющими нормальный закон распределения, в ячейке F33 рассчитайте линейный коэффициент корреляции Пирсона (функция PEARSON). В ячейке F34 вычислите значение квадрата коэффициента корреляции Пирсона и сравните его с коэффициентом детерминации, приведенном на графике.
3.Вычислите ранговый коэффициент корреляции Спирмена, который используется для оценки силы связи между двумя числовыми переменными, имеющими произвольный закон распределения. Он вычисляется по формуле:
|
|
n |
R |
)2 |
|
6 |
(R |
|
|||
|
|
1i |
2i |
|
|
r 1 |
|
i 1 |
|
|
, |
|
|
|
|
||
S |
n3 n |
|
|
||
|
|
|
|
||
где n = 30 – размер выборки, R1i и R2i – средние ранги 1ой и 2ой переменных.
Теоретические сведения.
Рангом наблюдения называют порядковый номер, который получит это наблюдение в упорядоченной по возрастанию (ранжированной) совокупности всех значений выбранной переменной. Если имеются элементы выборки, которые имеют одинаковое значение, они называются связкой. Количество одинаковых значений в связке – размер связки. Средний ранг – среднее арифметическое рангов элементов связки, которые бы они имели, если бы одинаковые элементы связки оказались различны. Например:
7
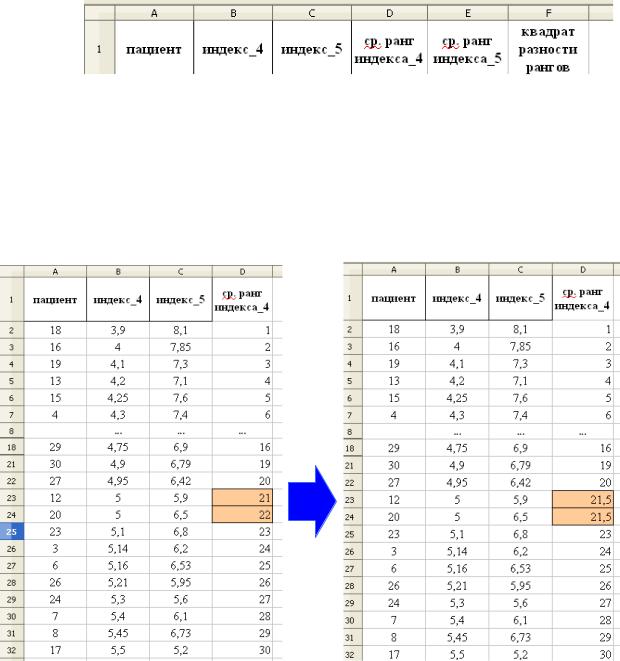
Для вычисления средних рангов переменных «индекс_4» и «индекс_5» добавьте в заголовки столбцов таблицы дополнительные наименования по образцу: При записи длинных названий переменных используйте опцию Переносить по словам из меню
Формат / Ячейки / Выравнивание.
Ранжирование переменных производится в следующем порядке:
1)Вся таблица сортируется по возрастанию переменной «индекс_4».
2)В столбце «ср.ранг индекса_4» методом автозаполнения вставляются порядковые номера (от 1 до
30)измерений в ранжированном ряду переменной «индекс_4».
3)С помощью заливки ячеек, выделяют связки и вычисляют средние ранги. Например, для переменной «индекс_4» есть только одна связка при значении «5» - порядковые номера 21 и 22. Следовательно, средний ранг будет равен =(21+21)/2=21,5.
4)Ранжирование переменной «индекс_5» проведите в той же последовательности: сортировка (по возрастанию) таблицы по переменной «индекс_5»; выявление связок и замена порядковых номеров чисел в связках их средними рангами.
5)В колонке F вычислите квадраты разностей средних рангов. Например, в ячейке F2 будет стоять формула: =(D2 – E2)^2, которая протяжкой копируется на весь столбец.
6)В ячейке F33 вычислите сумму квадратов разностей средних рангов (сумму по столбцу F).
7)По формуле для коэффициента корреляции Спирмена вычислите его значение в ячейке F34.
8)Сравните вычисленные коэффициенты корреляции Пирсона и Спирмена между собой. Их равенство характерно для ситуации, когда законы распределения обеих переменных нормальны. В противном случае, как правило, их значения будут сильно различаться.
8

Задание 3. Сравнение средних двух выборок с нормальным законом распределения.
Откройте файл «статистика_2(шаблоны для сравнения средних).ods» и сохраните его в свою рабочую папку под новым именем.
Проверьте значимость различия средних переменных «индекс_4» и «индекс_6» с помощью критерия Стьюдента. Воспользуйтесь шаблоном на листе «сравнение средних 1».
1)В ячейках B33:C33 рассчитайте количество наблюдений по каждой из сравниваемых переменных (используйте функцию COUNT).
2)В ячейках B34:C34 рассчитайте средние значения ( xi ) каждой из сравниваемых переменных (используйте функцию AVERAGE).
3)В ячейках B35:C35 рассчитайте дисперсии ( Si2 ) каждой из сравниваемых переменных (используйте функцию VAR).
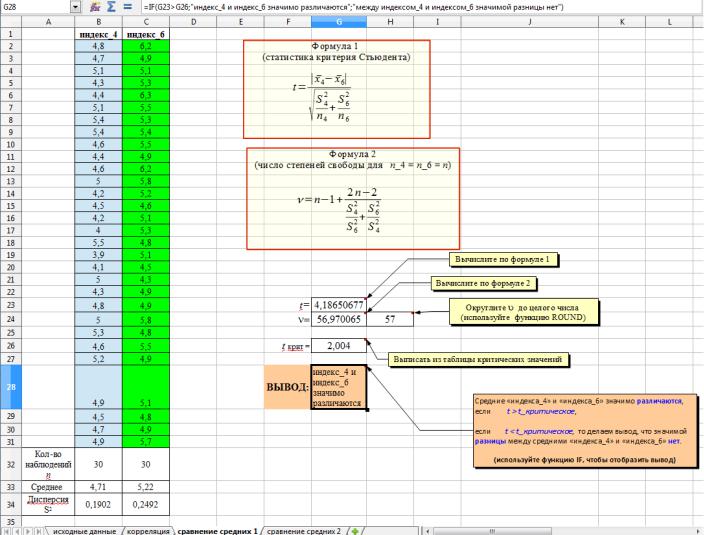
4)В ячейке G23 рассчитайте вычисленное значение статистики критерия Стьюдента (t) по
формуле:
| ̅ ̅|
√
5)В ячейке G24 рассчитайте число степеней свободы ( ) для табличного (критического) значения критерия Стьюдента по формуле:
6)В ячейке H24 округлите значение степеней свободы ( ) до целого числа (используйте функцию ROUND).
7)В ячейку G26 запишите критическое значение статистики критерия Стьюдента, соответствующее рассчитанному числу степеней свободы ( ) и уровню значимости = 0,05.
Чтобы найти tкритическое воспользуйтесь таблицей из файла «Критические значения критерия Стьюдента.ods».
8)В ячейке G28 используйте функцию IF, чтобы отобразить вывод относительно значимости разницы средних значений переменных «индекс_4» и «индекс_6»:
Если вычисленное значение статистики критерия Стьюдента (t) больше табличного
(tкритического), то необходимо сделать вывод, что переменные значимо различаются; Если же вычисленное значение статистики критерия Стьюдента (t) меньше или
равно табличного (tкритического), то необходимо сделать вывод, что значимой разницы между переменными нет.
Для самоконтроля см. рис. на следующей странице:
9
10
