9. Определение нормального закона распределения. Вывести формулу для вероятности попадання значений нормально распределенной св з заданный промежуток. Следствие. Правило «три сигма».
Нормальный закон
распределения. Определение.
СВ Х подчиняется нормальному закону
распределения (НЗР), если ее дифференц.
функция распределения имеет вид
,
где
- параметры распределения и имеют след.
вид: а=М(Х),
.
Теорема.
Математическое ожидание СВ X, распределённой
по нормальному закону, равно параметру
а этого закона, а её дисперсия - квадрату
параметра
,
т.е. М(Х)=а,
.
Попадание в
промежуток. Вероятность
попадания нормально распределенной
СВ Х в промежуток [x1;x2]
находится по формуле: Р(x1≤X≤x2)=
.
Доказательство.
Р(х1
х2)=F(х2)-F(x1)=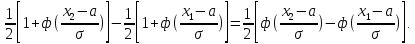
Рассмотрим частный
случай, когда точки х1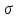=а-t
,
х2=а+t
симетричны относительно точки а. Найдем
вероятность попадания СВ Х в промежуток
(а-t
;
а+t
).
Р(а-t
≤Х≤а+t
)=
=
.
Неравенство
а-t
≤Х≤а+t
эквивалентно неравенству
≤t
.
Получили следующую формулу: Р(
≤t
)=
Обозначим t
Р(
≤
)=
Подложим в ф-лу
t=1,2,3.
t=1, Р(
≤
)=
=0,6827;
t=2, Р(
≤
)=
=0,9545;
t=3, Р(
≤
)=
=0,9973.
Вероятность в последнем равенстве близка к 1, поэтому справедливо утверждение, называемое правилом «три сигма».
Следствие (правило
«Три сигма»).
Если СВ X распределена нормально (с
параметрами а и
),
то практически достоверно, что абсолютная
величина её отклонения от М(Х) не
превосходит утроенного
,
т.е. Р(
≤
)
Т.о., если СВ X имеет
нормальный закон распределения с
параметрами а и
,
то практически достоверно, что её
значения заключены в интервале [a-3σ;
a+3σ]
Доказательство.
Р(
≤
)=
=2ф(3)=2*0,59865=0,9973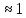
1. Центральная предельная теорема. Вывести интегральную теорему Муавра-Лапласа
2. Определение дифференциальной функции распределения. Доказать свойства.
3. Классическое определение вероятности события. Св-ва вероятности. Теорема умножения и ее св-ва.
4. Выведение формул для математического ожидания, дисперсии, среднего квадратического отклонения, частости и относительной частоты в схеме независимых повторных испытаний.
5. Математическое ожидание ДСВ и ее св-ва. 3св-ва доказать на выбор.
6. Определение интегральной функции распределения и доказательство ее св-в.
7. Доказать теоремы: «Формула полной вероятности», «Формула Байеса».
8. Дисперсия ДСВ и ее св-ва. 3 на выбор доказать.
9. Определение нормального закона распределения. Вывести формулу для вероятности попадания значений нормально распределенной СВ в заданный промежуток. Следствие. Правило 3-сигма.
10. Доказать теорему: «Сумма вероятностей и следствия из нее»
11. Схема применения критерия Пирсона.
12. Декомпозиция дисперсии. Коэффициент детерминации.
13. Точечные оценки выборки и осн. требования к ним.
14. Критерий независимости двух дискретных и непрерывных СВ. Кореляционнный момент. Коэффициент корреляции и его св-ва.
15. Простые и сложные статистические гипотезы. Ошибки первого и второго рода.
16. Определение статистической и корреляционной зависимости. Как определяется сила корреляционной зависимости.
17. Статистические гипотезы.
18. Выборочная дисперсия.
19. Выборочная средняя арифметическая.
20. Выправляная дисперсия. Условие, которое они удовлетворяют.