Завдання:

Варіант1

1. Задано вектори:

Знайти ; .

2. Знайти напрямні косинуси вектора .

3. Знайти об’єм піраміди ABCD, якщо

4.Знайти кут між векторами і , якщо

Варіант 2

_{1. Задано вектори:}

Знайти .

2. Знайти напрямні косинуси вектора .

3. Знайти об’єм піраміди ABCD, якщо .

4. Знайти кут між векторами і , якщо

Варіант 3

_1. Задано вектори:

Знайти .

2. Знайти напрямні косинуси вектора .

3. Знайти об’єм піраміди ABCD, якщо .

4.Знайти кут між векторами і , якщо

Варіант 4

_1. Задано вектори:

Знайти .

2. Знайти напрямні косинуси вектора .

3. Знайти об’єм піраміди ABCD, якщо .

4.Знайти кут між векторами і , якщо

Варіант 5

_1. Задано вектори:

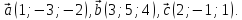
Знайти .

2. Знайти напрямні косинуси вектора .

3. Знайти об’єм піраміди ABCD, якщо .

4.Знайти кут між векторами і , якщо

Варіант 6

_1. Задано вектори:

Знайти .

2. Знайти напрямні косинуси вектора .

3. Знайти об’єм піраміди ABCD, якщо A.

4.Знайти кут між векторами і , якщо

Варіант 7

_1. Задано вектори:

Знайти .

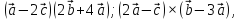
2. Знайти напрямні косинуси вектора .

3. Знайти об’єм піраміди ABCD, якщо .

4.Знайти кут між векторами і , якщо

Варіант 8

_1. Задано вектори:

Знайти .

2. Знайти напрямні косинуси вектора .

3. Знайти об’єм піраміди ABCD, якщо .

4.Знайти кут між векторами і , якщо

Варіант 9

_1. Задано вектори:

Знайти .

2. Знайти напрямні косинуси вектора .

3. Знайти об’єм піраміди ABCD, якщо .

4.Знайти кут між векторами і , якщо

Варіант 10

_1. Задано вектори:

Знайти .

2. Знайти напрямні косинуси вектора .

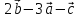3. Знайти об’єм піраміди ABCD, якщо .

4.Знайти кут між векторами і , якщо

Практична робота №4

Тема: Пряма лінія, її рівняння на площині та в просторі.

Мета: Відпрацювати навички записі рівнянь прямої на площині та в просторі.

Завдання: Виконати завдання згідно вашому варіанту. Оформити роботу. Відповісти на контрольні запитання.

Зміст звіту: 1. Тема роботи. 2. Мета роботи. 3. Завдання до роботи. 4. Порядок виконання завдань. 5. Підсумки виконання роботи.

Теоретичні відомості

Рівняння лінії в системі координат

Всякій лінії на площині , яка розглядається як геометричне місце точок, відповідає деяке рівняння, яке пов’язує координати будь-якої точки(так званої “біжучої” точки), яка розташована на цій лінії. При підстановці координат будь-якої точки, що належить цій лінії, в її рівняння, це рівняння перетворюється в тотожність (задовольняється). Якщо ж в рівняння лінії підставити координати будь-якої точки, яка не належить цій лінії, рівняння не задовольняється (обертається в нерівність).

При знаходженні рівнянь геометричних місць (ліній) інколи виявляється більш зручним виразити Декартові координати і довільної точки цього геометричного місця через деяку допоміжну величину (параметр), тобто представити  і  у вигляді

Така форма запису рівняння лінії називається параметричною, а рівняння системи називаються параметричними рівняннями даної лінії.

Виключення параметра  із системи (якщо воно можливе) приводить до рівняння, яке пов’язує і, тобто до рівняння лінії в Декартових прямокутних координатах виду.