Д разбиение не скорректированной системы

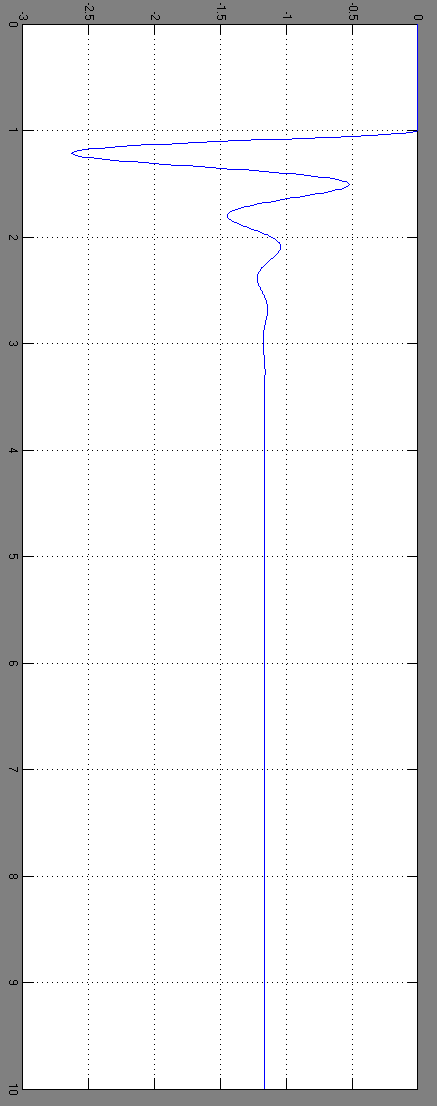
Построим переходный процесс не скорректированной системы, для чего необходимо взять коэффициент усиления разомкнутой системы из области устойчивости, то есть меньше чем 18,50. Возьмём коэффициент усиления равным: К = 15.

Заданный закон изменения возмущающего воздействия f(t)=1(t)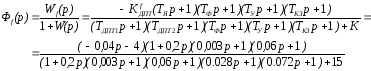

13. Синтез последовательного корректирующего звена методом логарифмических частотных характеристик

1. передаточная функция

где

т.к. ато вычислив, получим:

Определим частоты сопряжения и отметим их на графике

Отмечаем эти частоты на графике и начинаем построение ЛАЧХ следующим образом:

• первая асимптота от =1 до₁с угловым коэффициентом 0 дБ/дек, при этом эта прямая при= 1, пройдет через точкуL(1)=20log(K)=63,52 дБ;

• вторая асимптота от ₁до₂с угловым коэффициентом20 дБ/дек;

• третья от₂до₃с угловым коэффициентом40 дБ/дек;

• четвёртая от₃до₄с угловым коэффициентом60 дБ/дек;

• пятая от₄до₅с угловым коэффициентом80 дБ/дек;

• шестая от₅до бесконечности с угловым коэффициентом100 дБ/дек.

То есть на каждой сопрягающей частоте кривая ЛАЧХ изламывается на 20 дБ/дек.

ЛФЧХ имеет вид:

2. Для заданной системы определим основные показатели качества регулирования

M=1,2

Ϭ=22[%]

t_пер=0,8 [c]

Находим из графиков:

U_max=1,1

Теперь необходимо выбрать _ср, как _ср = (0,6  0,9)_П, но получившееся значение частоты среза не удовлетворяет условию времени регулирования, поэтому мы будем сдвигать частоту среза вправо до тех пор пока переходный процесс не будет заканчиваться за требуемое время. Выберем частоту среза равной 100, с^-1.

3. Находим из графика:

Запас устойчивости по амплитуде

G_max = 20lg=15,56 дБ; G_min = 20lg= 5,26 дБ;

запас устойчивости по фазе

=arccos=28,22

Строим ЛАЧХ корректирующего устройства.

L_КУ() =Lck()L().

По полученной L_КУ() записываемW_КУ(p):

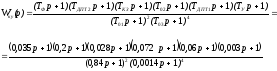
Проверим условие физической реализуемости ПКУ: степень полинома числителя mдолжна быть меньше или равна степени полинома знаменателяn. В нашем случаеm=6,n=6 то естьmn условие выполняется, следовательно ПКУ реализуемо.

Уравнения САР

После синтеза КУ, запишем :

Передаточная функция исходной системы (разомкнутой):

Передаточная функция синтезированного корректирующего устройства:

Передаточная функция разомкнутой скорректированной системы

Передаточная функция замкнутой скорректированной системы по задающему воздействию:

Передаточная функция замкнутой скорректированной системы по возмущающему воздействию:

Передаточная функция замкнутой скорректированной системы по ошибке:

Синтезируем принципиальную схему последовательного корректирующего звена и выполним расчёт его параметров.

.

В предыдущем пункте был произведен синтез КУ методом логарифмических частотных характеристик, и получена передаточная функция корректирующего устройства. В данном разделе работы рассматривается вопрос синтеза КУ на элементной базе и выбор параметров элементов. Для начала записывается передаточная функция корректирующего устройства:

Данную функцию необходимо разбить на звенья таким образом, чтобы каждое можно было реализовать на типовых звеньях. Разобьем её следующим образом:

где k_ку3­  k_ку6  коэффициент усиления электронного усилителя, в нашем случае все эти коэффициенты равны 1.

Производится выбор звеньев для реализации записанных функций. Опишем последовательно все звенья. Для начала произведем расчет всех пассивных звеньев: W_ку1(р) и W_ку2(р).

Для их реализации выбираем следующую структуру:

Передаточная функция данного звена имеет вид:

где:

Данное звено обеспечивает наклон характеристики только на 20, дБ, поэтому первое звено КУ будет состоять из двух таких звеньев, соединённых последовательно, вследствие чего передаточная функция звена будет иметь следующий вид:

Подбирая элементы R₁, R₂, и C добиваемся того, чтобы номиналы элементов соответствовали стандартным, например из ряда E24.

После подбора, получаем для W_ку1(p):

C = 1,3, мкФ; R₁ = 0,39 ,МОм; R₂ = 0,16, МОм.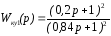

Для W_ку2(p) получаем:

C₁ = 1,2 ,мкФ; R₁ = 0,12 , МОм; R₂ = 63 ,кОм.

Теперь нам необходимо поднимать частотную характеристику, т.е. изламывать её вверх. Для этого используем активную цепочку на операционном усилителе с коэффициентом усиления равным единице:

Передаточная функция данного звена выглядит следующим образом:

где:

Выбирая элементы для k_ку3 = 1, получим:

C₁ = 1,2, мкФ; С₂ = 0,19 ,мкФ; R₁ = 5, кОм; R₂ = 7,5, кОм.

Как видно, данное звено инвертирует сигнал, следовательно в КУ должно содержать чётное число таких звеньев, либо иметь звено, которое инвертировало бы сигнал обратно. В нашем случае КУ имеет чётное количество инвертирующих звеньев.

Для W_ку4(p) получаем:

C₁ = 1,3, мкФ; C₂ = 5,3*10^-2, мкФ; R₁ = 27, кОм; R₂ = 27, кОм.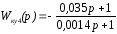

Для W_ку5(p) получаем:

C₁ = 1,2, мкФ; C₂ = 0,13, мкФ; R₁ = 6, кОм; R₂ = 11, кОм.

Для W_ку5(p) получаем:

C₁ = 1,1, мкФ; C₂ = 0,39, мкФ; R₁ = 3, кОм; R₂ = 3,6, кОм.

После определения номиналов всех звеньев, запишем передаточную функцию всего КУ:

А это в точности повторяет исходную функцию корректирующего устройства. Ниже представлена принципиальная схема корректирующего устройства реализованного на рассмотренных звеньях.

Произведем проверку правильности выбора структуры КУ. Для этого построим ЛАЧХи всех звеньев в отдельности, а затем просуммируем их (см. ниже). Полученная кривая сравнивается с кривой, полученной при синтезе корректирующего устройства методом ЛАЧХ. Из рисунков видим, что данные кривые совпадают, из чего можно сделать вывод, что структура КУ выбрана и рассчитана верно.

Принципиальная схема корректирующего устройства

18. Построение переходного процесса скорректированной системы

После корректировки системы, необходимо проверить, удовлетворяет ли она заданным качествам регулирования, для этого строится переходный процесс. Заданный закон изменения возмущающего воздействия f(t)=1(t)

19. Оценить основные показатели качества регулирования и устойчивости скорректированной САР.

По графику переходного процесса производится оценка основных показателей качества переходного процесса. Для этого отмечается на графике трубка шириной 2, где 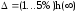, т.е. для данной системы = 210^-5… 10^-4.

Запишем основные показатели качества:

время регулирования:

перерегулирование: ,

19. Построим область устойчивости в плоскости коэффициента усиления разомкнутой скорректированной системы.

После синтеза корректирующего устройства необходимо дополнительно убедиться в устойчивости системы. Для определения максимального коэффициента усиления разомкнутой системы К_гран, произведем Д – разбиение в плоскости коэффициента усиления разомкнутой скорректированной системы.

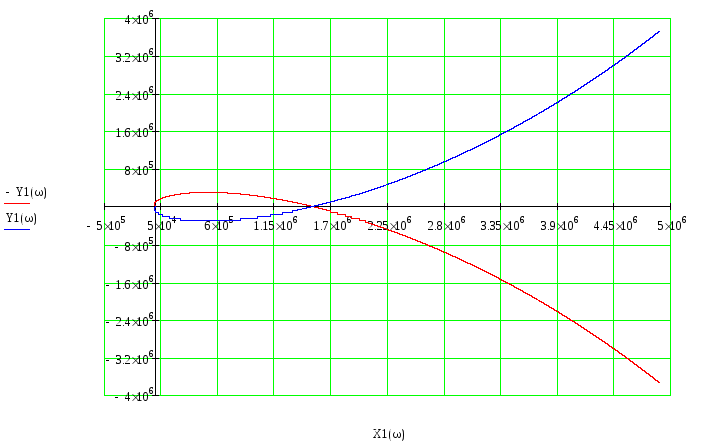
Положим p = j:

Строим на ЭВМ Д  разбиение. По этому графику определяется

K_гран: K  [0 … 1,6*10⁶]. Как видим коэффициент усиления разомкнутой системы принадлежит допустимым значениям. Из этого делается вывод, что в замкнутом состоянии система будет устойчива

19. Анализ достигнутых в скорректированной системе показателей качества регулирования.

Сравним полученные и заданные показатели:

При заданном законе возмущающего воздействия f(t) = 1(t) и при заданных показателе колебательности М = 1,4 и статической ошибке регулирования _ст = 0,2, %, удалось достичь:

Время регулирования: t_p = 0,77, c, при t_p = 0,8, с.

Перерегулирование:  = 3,5, %, при перерегулировании не скорректированной системы  = 74,2, %.

Сравнивая полученные результаты, можем заключить, что полученные результаты удовлетворяют заданным, а по некоторым позициям достигнут некоторый запас. Этот запас необходимо иметь для того, чтобы не идеальность корректирующего устройства не вызывала выхода показателей качества регулирования за пределы заданных. Не идеальность КУ возникает из-за того, что элементы используемые в нем так же далеки от идеала.

Список литературы.

1.Бесекерский В.А., Попов Е.П. “ТАУ”. Москва 1975г.

2.Егоров К.В. “Основы теории автоматического управления”. Москва 1967г.

3.Юревич Е.И. “Теория автоматического регулирования”. Энергия С-ПБ 1975г.

50