ПРОПОРЦИОНАЛЬНО­ИНТЕГРАЛЬНЫЕ РЕГУЛЯТОРЫ

Статическую ошибку, возникающую при пропорциональном регулировании,

можно исключить, если кроме пропорционального ввести еще и интегральное звено. Последнее образуется путем постоянного суммирования ε за определенный промежуток времени и формирования сигнала управления, пропорционального полученной величине.

Математически этот процесс может быть описан следующей зависимостью:

где – коэффициент пропорциональности интегральной составляющей, а

Тu ' постоянная времени интегрирования, параметр настройки регулятора.

Если 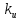0, то даже при незначительных отклонениях регулируемой величины сигнал со временем может достичь любой величины, что приведет к перемещению регулирующего органа до момента, пока ε не станет равным 0.

Рассмотрим физический смысл постоянной времени интегрирования. Предположим, что на вход регулятора поступил сигнал , а пропорциональная составляющая отсутствует ( = 0). При этом выходной сигнал будет меняться по закону

По истечении времени t = 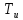значение выходного сигнала будет равно

(рис.1.13а).

Таким образом, постоянная времени интегрирования в ПИ-регуляторе равна времени, в течение которого с момента поступления на вход регулятора постоянного сигнала сигнал на выходе регулятора достигнет значения, равного значению входного сигнала.

Переходной процесс в ПИ-регуляторе показан на рис.1.13б. Устраняя статическую ошибку интегральный регулятор, однако, ухудшает качество переходного процесса. Поэтому на практике применяют комбинированные ПИ-регуляторы.

Рисунок 1 - Закон регулирования (а) и переходной процесс (б) при интегральном (И) регулировании.

При этом используется как параллельное соединение пропорционального и интегрального звена (рис.2а), так и последовательное соединение (рис.2б).

Рисунок 2 - Структурная схема идеальных ПИ-регуляторов.

ПИ-регулятор оказывает воздействие на регулирующий орган пропорционально отклонению и интегралу от отклонения регулируемой величины.

Для схемы на рисунке 2а частотная характеристика ПИ-регулятора имеет вид :

При скачкообразном изменении регулируемой величины на значение ε0 ПИ-регулятор со скоростью, определяемой быстродействием привода, перемещает исполнительный механизм на величину (), после чего исполнительный механизм дополнительно перемещается в ту же сторону со скоростью , пропорциональной отклонению регулируемой величины. Следовательно, в ПИ-регуляторе при отклонении регулируемой величины от заданного значения мгновенно срабатывает пропорциональная (статическая) составляющая регулятора, а затем постепенно увеличивается интегральная (астатическая) составляющая регулятора.

Переходная характеристика ПИ-регулятора для параллельного соединения на рисунке 2а показана на рисунке 3(прямая 1).

Рисунок 3 - Закон ПИ-регулирования регуляторов: 1 - для схемы на рисунке2а, 2 - для схемы на рисунке 2б.

Параметрами настойки являются независящие друг от друга коэффициенты усиления и постоянная времени интегрирования .

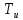Схема на рисунке 3б реализует закон регулирования

где – 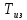постоянная времени изодрома.

Частотная характеристика ПИ-регулятора по схеме рисунке 3б имеет вид:

Таким образом, ПИ-регулятор со структурной схемой, приведенной на рисунке 3б, имеет взаимосвязанные параметры настройки статической и астатической частей по коэффициенту . Так, при настройке коэффициента усиления будет изменяться и постоянная времени интегрирования:

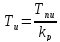
Рассмотрим физический смысл постоянной времени изодрома 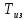. Предположим, что на вход регулятора поступил постоянный сигнал . Тогда

При поступлении на вход регулятора сигнала в начальный момент сработает пропорциональная составляющая и на выходе регулятора появится сигнал 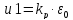. В дальнейшем линейно начинает нарастать выходной сигнал от интегральной составляющей и при достигнет значения .

– это время, в течение которого от начала действия интегральной (астатической) составляющей регулятора пропорциональная (статическая) составляющая удваивается. Переходной процесс при ПИ-регулировании показан на рисунке 4.

Рисунок 4 - Переходной процесс при пропорционально-интегральном регулировании.

ПИ-регулятор обеспечивает нулевую ошибку в установившемся состоянии.

Варианты структурных схем промышленных ПИ-регуляторов приведены на

Рисунке 5.

Рисунок 5 - Структурные схемы промышленных ПИ-регуляторов.

Выбирая ту или иную схему, можно подобрать наиболее подходящую структуру для Вашей задачи.

Рассмотрим следящую систему управления зеркалом телескопа, представленную на рисунке 6:

Исходные данные:

Электромеханическая постоянная времени ДПТ - Т_м = 0.3 с

Постоянная времени якоря ДПТ - Т_я = 0.015 с

Постоянная времени короткозамкнутой цепи ЭМУ - Т_кз = 0.06 с

Постоянная времени цепи управления ЭМУ - Т_у = 0.007 с

Постоянные времени последовательного корректирующего устройства:

T1 = 7.69 с

T2 = 2 с

T3 = 0.25 с

T4 = 0.059 с

T5 = 0.016 с

T6 = 0.007 с

T7 = 0.003 с

T8 = 0.281 с

T9 = 0.016 с

Коэффициент усиления скорректированной системы - К_sk = 77

Коэффициент усиления нескорректированной системы - К_nesk = 5

Коэффициент усиления ЭМУ - К_ЭМУ = 7

Коэффициент передачи редуктора - К_р = 0.075

Коэффициент усиления разомкнутой системы по возмущению - К^f= 0.039

Время регулирования - t_p = 1 с

Показатель колебательности - M = 1.2

Для составления функциональной схемы САР необходимо знать все элементы, из которых состоит система.

В следящей системе управления зеркалом телескопа используются сельсин-датчик СД, сельсин-приемник СП, фазочувствительный выпрямитель ФЧВ, электромашинный усилитель ЭМУ, двигатель постоянного тока ДПТ и редуктор Р.

Функциональная схема системы автоматического регулирования представлена на рисунке 7:

Рисунок 7 – Функциональная схема

Принцип работы системы.

Система находится в покое, когда заданное и фактическое положение телескопа соответствуют друг другу.

Для измерения угла рассогласования следящей системы применяются сельсины, работающие в трансформаторном режиме.

При повороте ротора сельсина-датчика на угол _вх на выходе сельсина-приемника создается напряжение соответствующей фазы и амплитуды.

Выходной сигнал сельсина-приемника поступает на фазочувствительный выпрямитель, задачей которого является преобразование входного переменного напряжения в постоянный ток, причем полярность выходного напряжения определяется фазой входного напряжения.

Выходной сигнал выпрямителя воздействует на обмотку управления электромашинного усилителя. Двигатель через редуктор воздействует на зеркало телескопа и управляет положением однофазной обмотки сельсина-приемника (ротор сельсина-приемника с помощью обратной связи возвращается в согласованное положение с ротором сельсина датчика и двигатель останавливается).

Если заданное и фактическое положения зеркала телескопа совпадают, то положения однофазных обмоток сельсинов одинаковы и система находится в покое. В противном случае система будет находиться в движении.

Процесс регулирования выглядит следующим образом:

_вх   ( = _вх - _вых)   U_оу   i_оу   U_дв   n_дв   _вых  

 ( = _вх - _вых) 

Структурная схема системы автоматического регулирования приведена на рисунке 8.

Построение переходных процессов в скорректированной и в нескорректированной системах.

Передаточная функция скорректированной системы имеет вид:

Передаточная функция скорректированной замкнутой системы имеет вид:

Схема, построенная в среде Matlab для нескорректированной системы (рисунок 9):

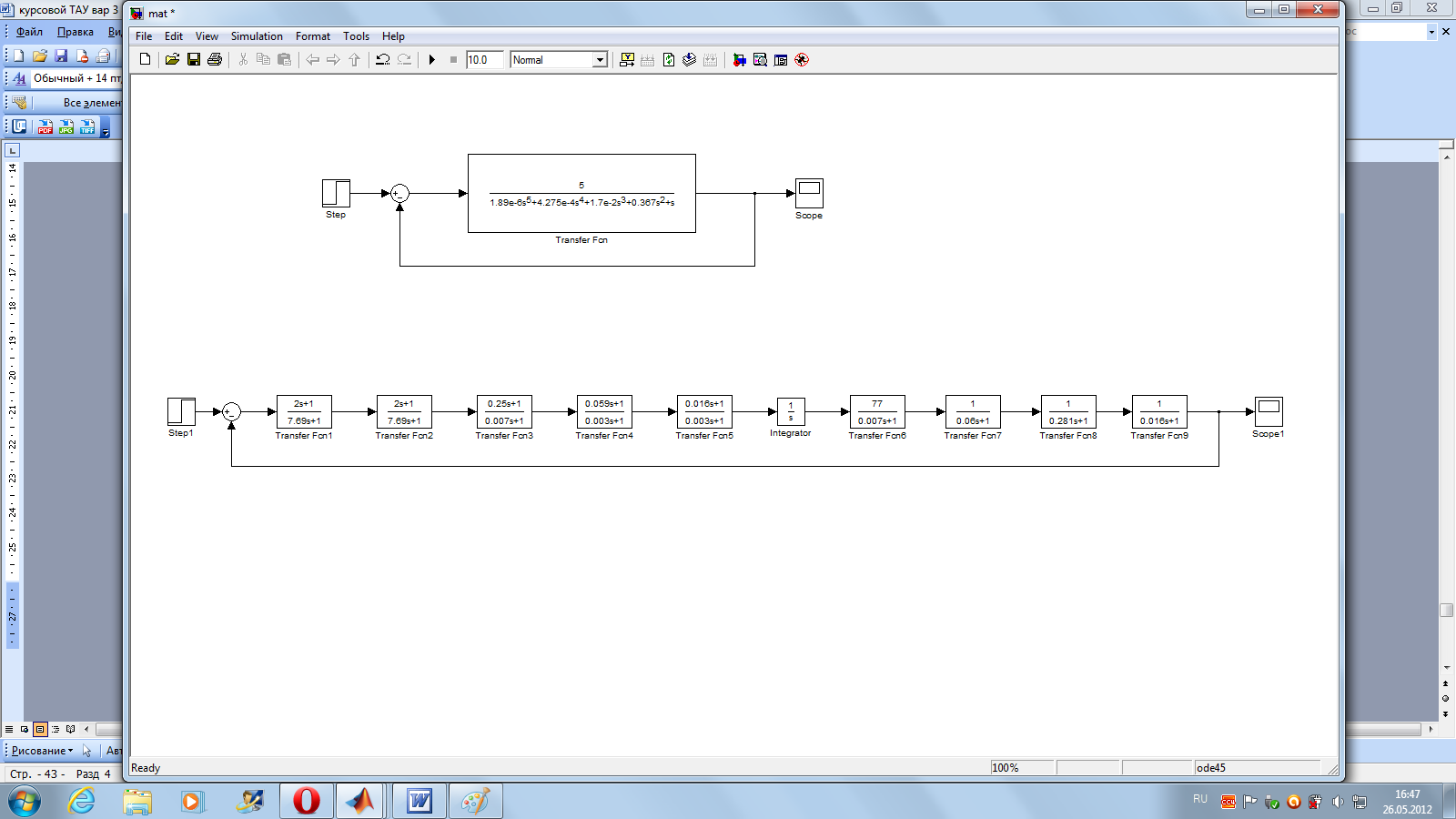
Рисунок 9 – Схема нескорректированной системы

Переходный процесс нескорректированной системы (рисунок 10):

Рисунок 10 – График переходного процесса нескорректированной системы

Схема, построенная в среде Matlab для скорректированной системы (рисунок 11):

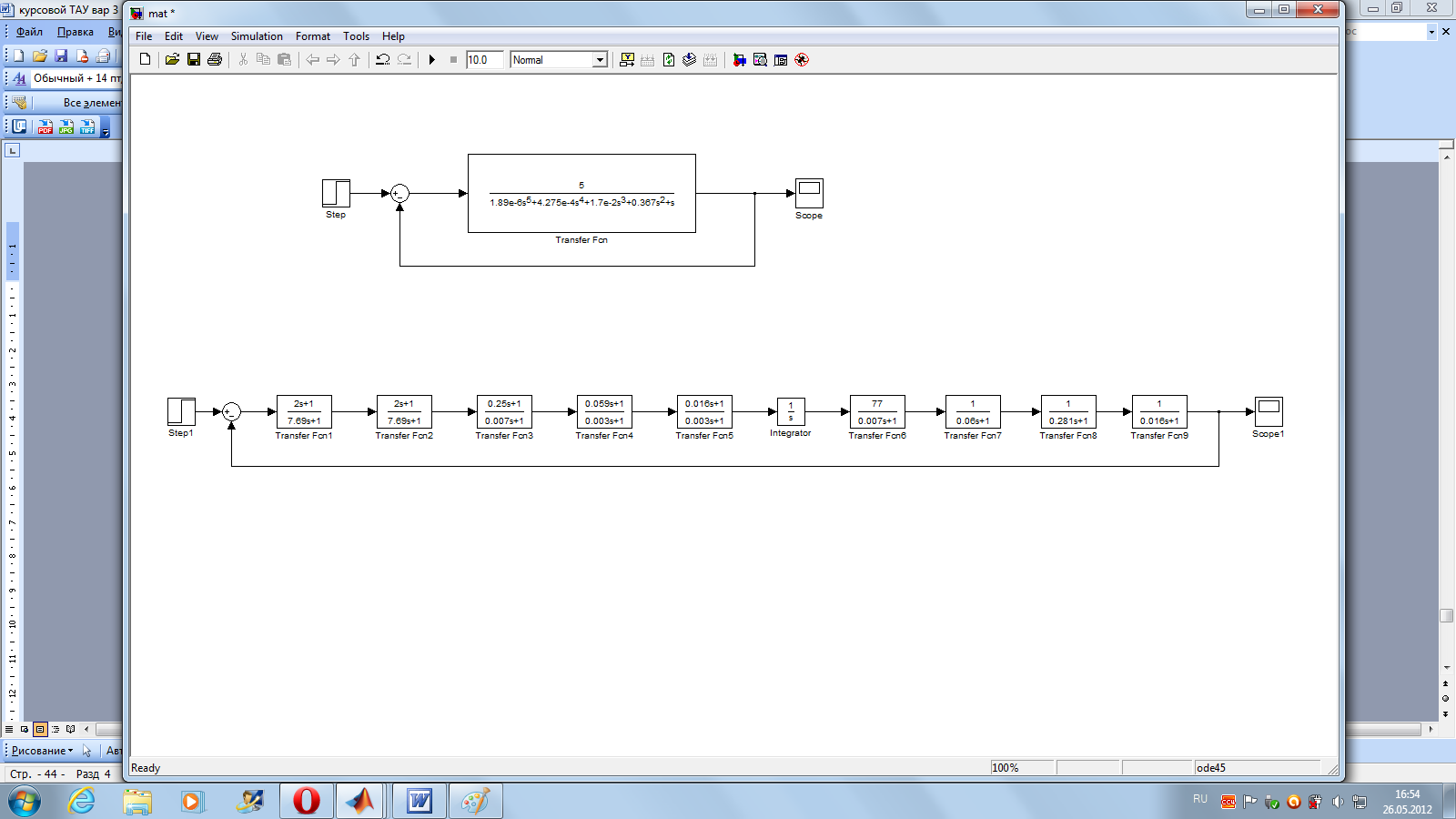
Рисунок 11 - Схема скорректированной системы

Переходный процесс скорректированной системы (рисунок 12):

Рисунок 12 - График переходного процесса скорректированной системы

Построение переходных процессов с ПИ-регулятором.

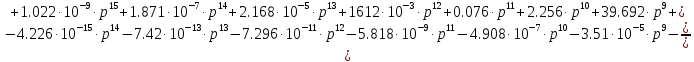
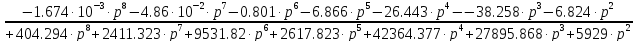
Схема САУ с ПИ-регулятором выглядит следующим образом:

Рисунок 13 – Схема САУ

Строим и моделируем схему в Matlab для передаточной функции.

Рисунок 14 - Схема с ПИ-регулятором.

Переходный процесс САУ с ПИ-регулятором представлен на рисунке 15:

Рисунок 15 – переходный процесс.