Лекции (doc) - 2008 / 5

§1. Стационарный режим политропического реактора.

 

1.1. Основные допущения

1.2. Микрокинетика процесса

1.3. Математическое описание процесса (прямоток)

1.4. Информационная матрица (прямоток)

1.5. Блок-схема алгоритма расчёта (прямоток)

1.6. Математическое описание процесса (противоток)

1.7. Информационная матрица (противоток)

1.8. Блок-схема алгоритма расчёта (противоток)

 

§2. Построение компьютерной модели трубчатого реактора в нестационарном режиме.

 2.1. Основные допущения

2.2. Уравнение математического описания

§1. Стационарный режим политропического реактора.

 

а) Теплоноситель движется в режиме прямотока (Задача Коши или задача с начальными условиями).

 

 б) Теплоноситель движется в режиме противотока (Краевая задача).

 

 1.1. Основные допущения:

 - микрокинетика: реакция

 

 

 

- движение потоков представляется гидродинамической моделью идеального вытеснения;

 - тепловые эффекты стадий не зависят от температуры;

 - при теплообмене между основным потоком и потоком в рубашке учитывается только теплопередача;

 - коэффициент теплопередачи = const.

 

1.2. Микрокинетика процесса

 

 

 Определить:

 

 

 

 

 

 

 

 

 

 

 

 Выбираем 2 ключевых компонента А и В

 

 

 

Стехиометрическое соотношение для неключевого компонента С:

  

 

 

  

 

 

1.3. Математическое описание процесса (прямоток).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Уравнение для потока теплоносителя:  

 

 

 

n+3 дифференциальных уравнений.

 

 Начальные условия:

 

 

 

 

 

 

 

 

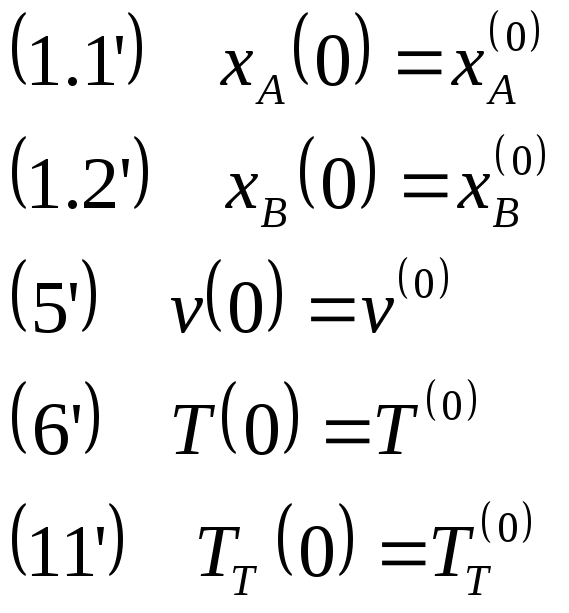
Для определения частного решения на компьютере решается задача Коши или задача с начальными условиями – см. теплообменник «вытеснение-вытеснение» (прямоток).

 

 

 

 

 

 

 

 

 

1.4. Информационная матрица (прямоток)

 

 

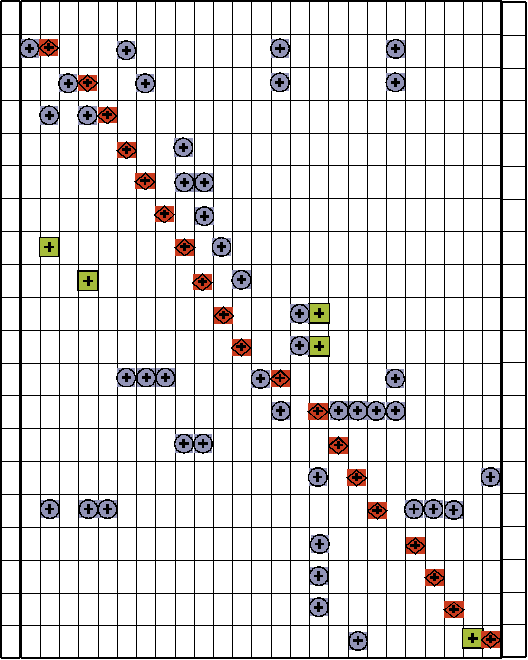
1.5. Блок-схема алгоритма расчёта (прямоток)

 

 

 

 

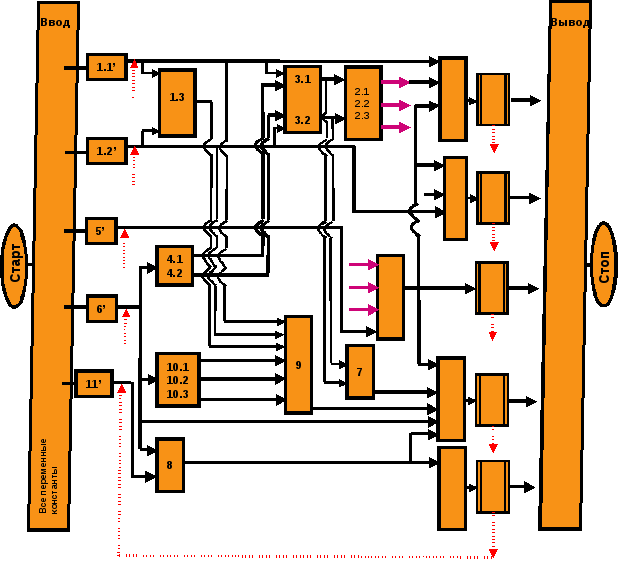
 1.6. Математическое описание процесса (противоток).

 

 

 

 

 

Модель идеального вытеснения, покомпонентный баланс:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

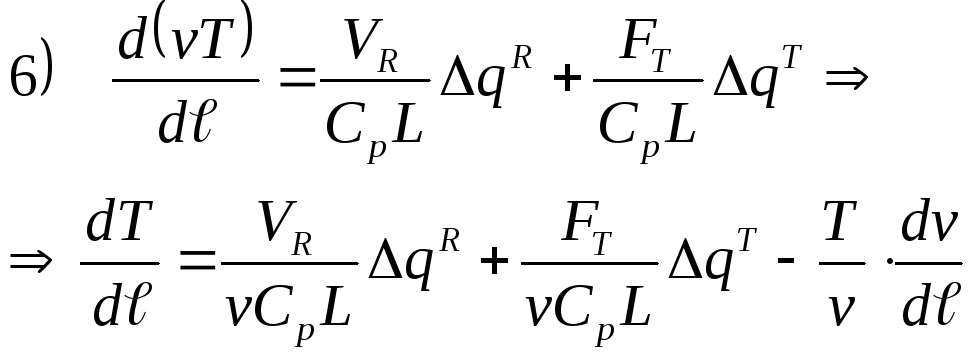
 Уравнение для потока теплоносителя:

 

 

 

  

n+3 дифференциальных уравнений, в сравнении с прямотоком изменилось только уравнение (11).

 

 Система начальных условий: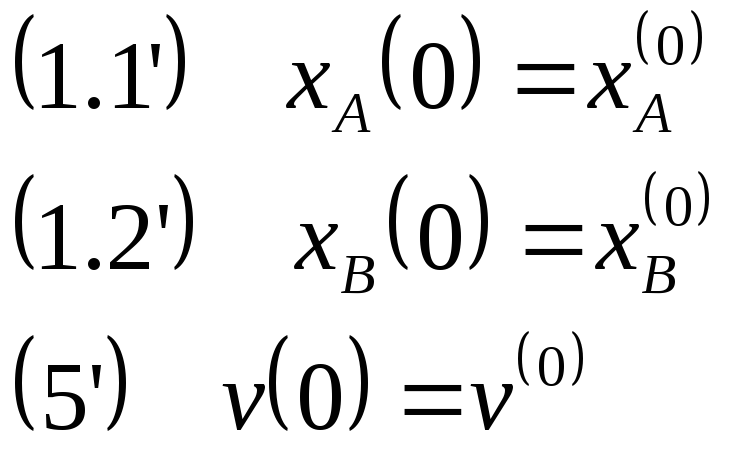

 

 

 

 

 

 

 

 Для определения частного решения на компьютере решается краевая задача с краевыми условиями – см. теплообменник «вытеснение – вытеснение» (противоток).

 

 

 

 

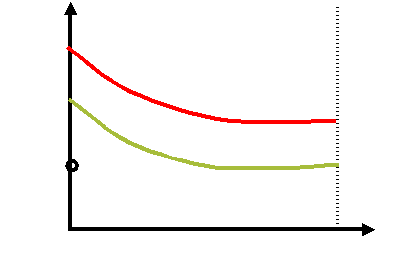
Начальное приближение:

 

 

Краевое условие превратилось в уравнение, которое определяет величину , т.е. величину температуры теплоносителя на входе.

 

1.7. Информационная матрица (противоток)

 

 

 

 

 

 

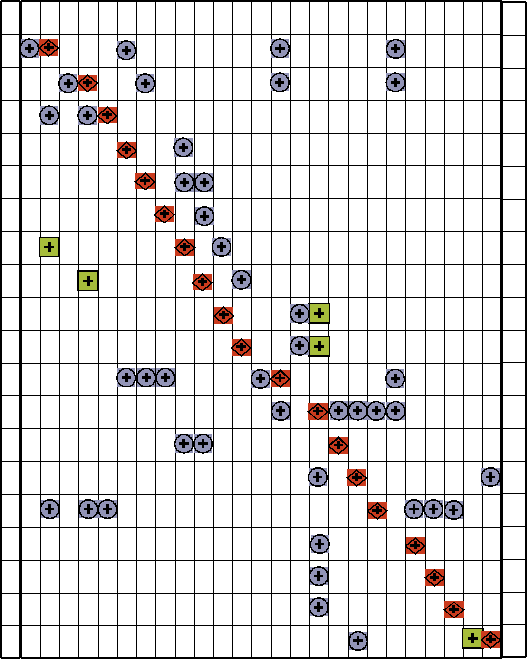
1.8. Блок-схема алгоритма расчёта (противоток)

 

 

 

 Решение уравнения 11’:

 

 

 

 §2. Построение компьютерной модели трубчатого реактора в нестационарном режиме.

 

 

 

2.1. Основные допущения:

 

• изотермический режим;

• однопараметрическая диффузионная модель.

 

2.2. Уравнение математического описания:

 

 

 

 

 

 

 

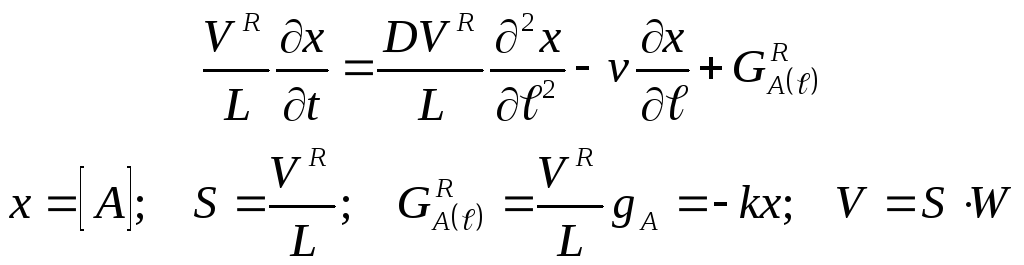
Уравнение 1) является дифференциальным уравнением в частных производных второго порядка параболического типа с двумя независимыми переменными t и и описывает нестационарный режим трубчатого реактора, в котором протекает единственная простейшая реакция, если принята однопараметрическая диффузионная модель для потока.

 

Необходимо найти:

 

 

 

 

 Начальное условие:

   

 

Граничные условия:

 

 

 

 

 

Для решения системы дифференциальных уравнений в частных производных (СДУЧП) может быть использован метод дискретизации, в соответствии с которым производные представляются в конечно-разностной форме в определённом интервале и/или [0, L] в результате чего уравнение 1) с начальным 1’) и граничными 1’’) условиями превращаются в систему обыкновенных дифференциальных уравнений (СОДУ) и/или в систему конечных уравнений (СКУ).

 

 Для этого уравнения можно использовать три варианта дискретизации:

 1) По независимой переменной  :

 

 

 

 

 

 

В результате получается система обыкновенных дифференциальных уравнений 1-го порядка с независимой переменной t .

 

 2) По независимой переменной t :

 

 

 

 

В результате получается система обыкновенных дифференциальных уравнений 2-го порядка с независимой переменной .

 

 3) По независимым переменным и t :

  

 

 

 

 

 

 

 

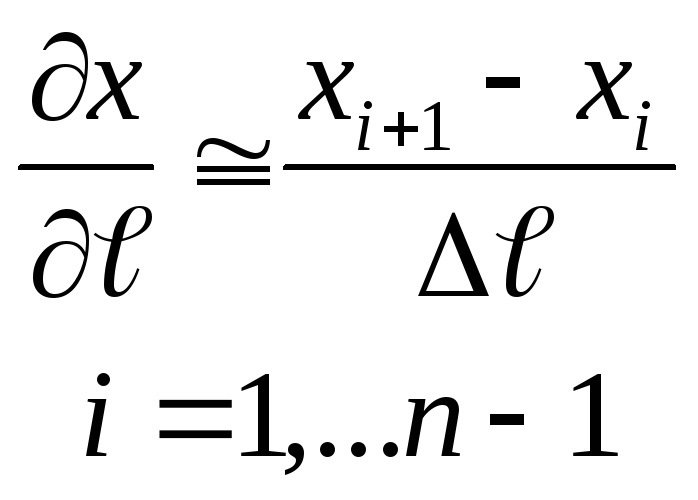
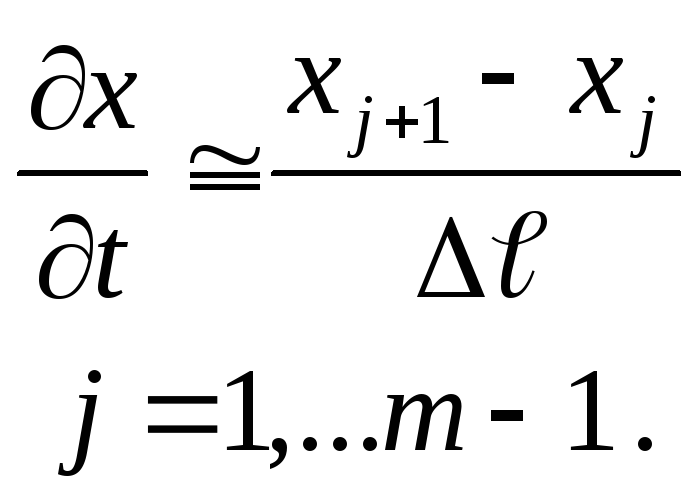
 В результате получается система конечных уравнений.

 Детально рассмотрим 1-й вариант дискретизации по независимой переменной :

 

 

 

 

 

При 0 < < L конечно-разностное представление производных имеет вид:

  - Производная «по недостатку»:

 

 

 

 - Производная «по избытку»:

 

 

  

 

 - Вторая производная:

 

 

  

 

 В этом случае граничные условия 1’’) равны:

 

 

  

 

В результате из одного уравнения в частных производных вследствие дискретизации получается система (n-1) обыкновенных дифференциальных уравнений с независимой переменной t и начальным условием 1’), представленным в дискретном виде:

 

  

 

 Если для конечно-разностного представления производной использовать «производную по избытку», то система обыкновенных дифференциальных уравнений с начальными условиями имеет вид:

  Преобразуя уравнение и

предполагая, что его параметры являются константами (D, W и k), можно получить следующую систему обыкновенных дифференциальных уравнений:

   

 

 

 

или

 

 

 

 

 

 

 

 

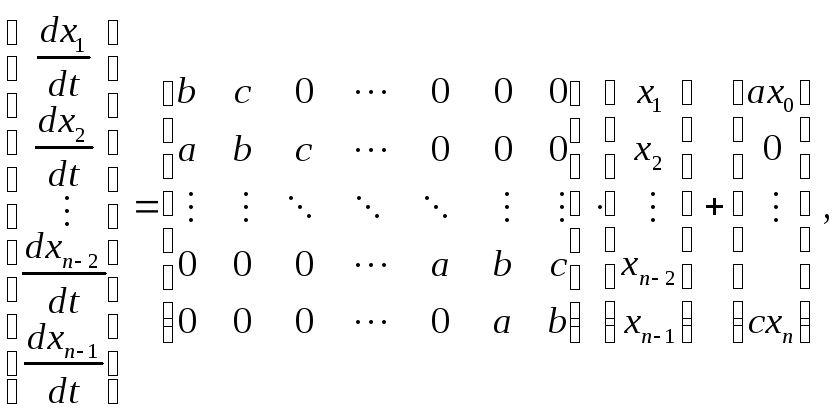
 где

 

 

 

 Из изложенного следует, что система уравнений включает граничные условия и в матричном виде может быть представлена:

 

 

 

 

где - вектор с граничными условиями, а начальные условия являются дискретным представлением начального условия

 

 

 

 

 

Полученная система неоднородных обыкновенных дифференциальных уравнений может быть легко решена любым из известных методов (например, методом Эйлера или Рунге-Кутта), тем более потому, что матрица её коэффициентов является трёхдиагональной.