Кинематический расчёт приводов главного движения с регулируемым электродвигателем»

Особенность расчёта привода с регулированием частоты вращения от электродвигателя состоит в необходимости подобрать механическую коробку скоростей и регулируемый двигатель (РД), которые бы обеспечили заданный диапазон регулирования частот вращения шпинделя с требуемыми параметрами.

Обычно РД (двигатели постоянного тока –ДПТ и асинхронные с частотным регулированием частоты вращения вала ротора - АД)) имеют сравнительно небольшой диапазон регулирования с постоянной мощностью (D_дв = 3 ÷ 6). Поэтому в приводах главногодвижения с РД для расширения диапазона регулирования добавляют механические коробки скоростей (КС). Наиболее часто в таких приводах встраивают коробки на две - четыре ступени регулирования (z_кс=2 ÷ 4).Частота РД изменяется бесступенчато, а за счет КС, кроме того можно обеспечить на выходе геометрический ряд. При расчете РД представляют как групповую передачу наступеней с рядом.

Диапазон регулирования на выходном валу (шпинделе станка) коробки скоростей равен:

D_z = D_kc∙D_дв , (1)

где: D_кс - диапазон регулирования механической КС;

D_дв - диапазон регулирования двигателя с постоянной мощностью.

Для обеспечения передачи полной мощности электродвигателя на шпиндель станка во всём диапазоне регулирования, принимают

D_kc ≈ D_дв (2)

На рисунке 1а показан вариант графика частот вращения для этого случая. Как видно из графика, на шпиндель (вал Ш) передаётся полная мощность от частоты n₁ до п₂. Если такой диапазон регулирования шпинделя не удовлетворяет требованиям к приводу главного движения, его можно увеличить путём изменения передаточного отношения i₂.

На рис. 16 передаточное отношение i₂ уменьшили до величины i'₂ (условие 0,25 ≤ i ≤2 должно выполняться). Тогда полная мощность на шпиндель могла бы передаваться в диапазоне п_р-п₂. Но расширение диапазона в данном случае, привело к"провалу" (уменьшению) мощности на некоторых частотах вращения в середине диапазона привода (частота п_т в промежутке п_i – п_j).

Такой "провал" нежелателен, но, в принципе, допустим, если он не превышает 10÷25% мощности привода.

В диапазоне n₁÷п_р (см. рис. 1(6)) привод работает при постоянном крутящем моменте на двигателе и, следовательно, переменной мощности. Уменьшение мощности привода в начале диапазона частот вращения шпинделя оправдано тем, что эти частоты используются реже (в отличие от частот середины диапазона). Поэтому при работе в диапазоне частот от n₁ до п_р производительность станка ниже из-за использования не полной мощности двигателя.

Пример расчёта привода с регулируемым электродвигателем

Исходные данные: привод главного движения должен обеспечить частоту вращения шпинделя n₁ = п_штmin = 40об/мин; п₁=п_шптах=2800 об/ мин; при знаменателе геометрической прогрессии φ = 1,12.

По результатам анализа технологических процессов, реализуемых на проектируемом станке и расчёта режимов резания определяют мощность, потребную на резание Р_рез. Задаваясь коэффициентом полезного действия (η = 0,8÷0,9) коробки скоростей, находят мощность двигателя. По ней подбирают двигатель. Пусть подобранный двигатель имеет следующие характеристики:

Тип электропривода "Мезоматик - V"

Тип двигателя V132L

Номинальная мощность, кВт - 15

Номинальная скорость, п_н, об/мин - 1000

Максимальная скорость, об/мин: при полной мощности, п_дртах - 3000

при снижении мощности, п_дтях - 5000

Номинальный момент, М_н, Н*м -143

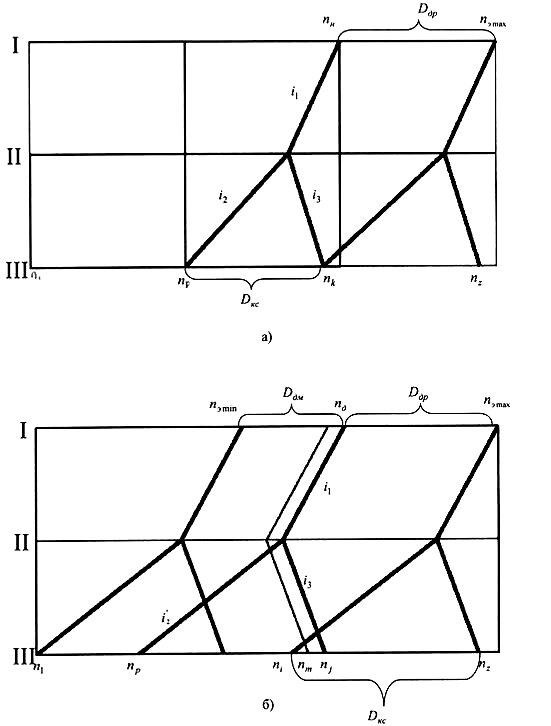
Рисунок 1. Графики частот вращения привода

Dкс- диапазон регулирования коробки скоростей; Dдp – диапазон регулировки двигателя с постоянной мощностью; Dдм - диапазон регулирования с постоянным моментом.

При расчёте коробок скоростей с регулируемыми электродвигателями используют следующие выражения:

- пределы передаточных отношений в группе передач

0,25 ≤ i ≤ 2 (3)

- расчётная частота вращения шпинделя

(4)

- диапазон регулирования частот вращения шпинделя с постоянной мощностью

(5)

- диапазон переключения в группе передач

(6)

(i_max = 2,i_min = 0,25)

- количество ступеней скорости механической коробки скоростей

(7)

Находим диапазон регулирования привода (шпинделя) по выражению:

_, об/мин

а расчётную частоту вращения шпинделя, об/мин:

об/мин

Примем п_р = 125 об/мин.

Тогда диапазон регулирования частот шпинделя с постоянной мощностью определится:

_.

Диапазон регулирования двигателя с постоянной мощностью:

Зададимся величиной передаточных отношений в группе передач, примем 0,25 ≤ i ≤ 2. Тогда диапазон переключения в группе будет равен:

Определим количество ступеней скорости в механической части привода:

Принимаем Z_K = 2.

Рассчитаем ряд частот вращения шпинделя по формуле:

Округлим его до стандартного (фактические числа оборотов шпинделя не должны отклоняться от стандартного более чем на ± 10 •(φ-1)%). Нанесем частоты на график (см. рис.2)

Определим максимальную частоту вращения вала II, задавшись значением i₃ = 2 (см. рис.2):

Нанесём передаточное отношение i₃ на график. Определим по графику i₁:

Определим частоту вращения шпинделя при частоте вращения двигателя n_д.р.мах и минимальном передаточном отношении коробки скоростей (i₂ = 0,25):

п_шп = 3000 • 0,466 • 0,25 = 350 об/мин

Найдем частоту вращения вала II при включении на шпинделе расчетной частоты

п_р = 125 об/мин :

n_{II min p} =125/0,25 = 500 об/мин.

При этом двигатель должен обеспечить частоту п_др = 500/0,466 = 1072 об/мин

На данной частоте двигатель развивает полную мощность, так как п_др > п_н.

Определим частоту вращения двигателя при включении n₁:

n_{Imin p} = n₁/(i₁ · i₂) = 40/(0,25 · 0,466) = 350 об/мин

В диапазоне частот от 1000 до 343 об/мин двигатель работает при постоянном моменте (М_н =143н/м)и переменной мощности. Ее величину рассчитывают по формуле, Вт:

(8)

где М_н - номинальный момент, Н·м;

п - частота вращения, об/мин

Рассчитаем мощность на шпинделе станка в пределах частот вращения двигателя от п_д = 1072 об/мин до п_д = 3000 об/мин. В этом диапазоне двигатель развивает полную мощность, поэтому

N_ш = N_н · η = 15 · 0,9 = 13,5 кВт

В промежутке частот вращения шпинделя лежащих между п = 350 об/мин и п = 1000 об/мин включается передаточное отношение i₃ коробки скоростей, а двигатель работает на частотах меньше номинальной (см. рис.2). Частоты двигателя меньше номинальной используются при включении передаточного отношения i₂ для получения частот вращения шпинделя в диапазоне 40-125 об/мин. Поэтому в пределах от 40 до 125 об/мин и от 315 до 1000 об/мин двигатель работает при постоянном моменте.

Таким образом, на шпинделе полная мощность, с учетом КПД, будет в диапазонах от 125 до 350 об/мин при передаточном отношении коробки i₂ = 0,25 и от 1000 до 2800 об/мин, при i₃=2.

Рисунок 2. График частот вращения привода при z_кс=2 (I,II,IIIвалы коробки скоростей)

Рисунок 3. График частот вращения привода при z_кс=4

В диапазоне от 600 до 890 об/мин получили "провал" мощности. На этом участке двигатель работает при постоянном моменте, и мощность на шпинделе рассчитываем по формуле (8).

Анализ графика показывает, что величина "провалов" мощности на частотах 400÷630 об/мин превышает допустимый предел в 20 % (2,7 кВт). Очень малые мощности получаются при вращении шпинделя на малых частотах (от 40 до 112 об/мин). Поэтому в коробке скоростей следует приблизить диапазон регулирования коробки скоростей к диапазону регулирования двигателя с постоянной мощностью (условие (2)). Для уменьшения «провалов» мощности на шпинделе станка введем следующие изменения в коробке скоростей:

а) увеличим i₂ до величины, позволяющей получать частоту вращения п_ш = 705 об/мин (i₂ = 705/1400 ≈ 0,5); на рис. 2 это передаточное отношение показано пунктиром);

б)введем ещё одну группу передач в механическую часть привода.

График частот вращения для этого варианта (при количестве ступеней в коробке скоростей равном 4), показан на рис. 3.

Здесь в первой группе передач выбраны передаточные отношения i`₂ =0,5 (вместо i₂ = 0,25 , см. рис. 2), i₄ = 1 и i₅ = 0,25. Полная мощность (13,5 кВт) может использоваться в пределах частот вращения шпинделя 63÷180 об/мин, 250÷705 об/мин, 1000÷2800 об/мин. В диапазонах от 40 до 63 об/мин, от 180 до 250 об/мин, от 705 до 1000 об/мин двигатель работает при постоянном моменте, падение мощности на шпинделе имеет место, но находится в допустимых пределах. Так на частотах от 40 до 63 об/мин мощность привода уменьшается до 9 - 12,1 кВт, что допустимо.

Выбранный двигатель VI32 и электропривод "Мезоматик - V" позволяют разгонять двигатель до частоты п = 5000 об/мин при снижении мощности (см. характеристики привода). Это открывает возможность иметь на шпинделе частоты вращения в пределах 2800÷4500 об/мин при уменьшенной мощности привода. Следовательно, при чистовых режимах обработки, когда необходимость в использовании полной мощности на шпинделе отпадает, можно включить указанные частоты. Фактический диапазон регулирования привода увеличивается до значения D_z = 4500/40 ≈ 112.

После определения из графика передаточных отношений, рассчитывают числа зубьев зубчатых колес.

Приведенная в приложении I таблица облегчает проведение расчетов. В ней по горизонтали отложена сумма зубьев, а по вертикали - передаточные отношения, кратные 1,06. Пустые клетки означают, что при данном значении ΣZ передаточное отношение не может быть выдержано в требуемых пределах ± 10·(φ - 1) %, в остальных клетках указано число зубьев меньшего зубчатого колеса.

Порядок расчетов следующий:

а) По графику частот вращения для первой группы передач находим:

б) Зададимся суммой зубьев ΣZ = 54.

в) На пересечении строки с числом 2 и столбца ΣZ = 54 находим Z₁ =18, тогда: Z₂ =54-18 = 36.

Аналогично находим числа зубьев других колес. Результаты расчетов чисел зубьев зубчатых колес в передачах коробки скоростей приведены в таблице 1.

Таблица 1 - Расчетные значения чисел зубьев колес коробки скоростей (φ = 1,12)

РАЗРАБОТКА КИНЕМАТИЧЕСКОЙ СХЕМЫ КОРОБКИ СКОРОСТЕЙ

Кинематический расчет завершается вычерчиванием кинематической схемы коробки скоростей. В качестве исходных данных используем график частот вращения (см. рис. 5.1) и кинематическую схему базового станка. На

схеме (рис. 5.5) указываются номера валов, характеристика электродвигателя, числа зубьев колес. Кинематическая схема должна вычерчиваться в соответствии с требованиями ГОСТ.

Некоторые рекомендации по взаимному расположению

зубчатых колес трехступенчатого блока

При перемещении подвижного тройного блока на валу II (см. рис. 5.5) колеса, расположенные сверху и снизу от среднего (большего) колеса, проходят мимо среднего колеса, закрепленного на валу Ш. Чтобы зубья этих колес не зацеплялись и блок свободно перемещался при переключении скоростей, должны выполняться условия (рис. 5.6):

(5.4)

где Z Σ – суммарное число зубьев средних колес. В нашем примере эти условия выполняются, так как ( 56 + 25 ) < [(56 + 39 ) – 4] ; (56 + 32. ) < [(56 + 39) – 4].

Рис. 5.5. Кинематическая схема коробки скоростей

Рис. 5.6. Наиболее простая компоновка группы передач с тройным блоком

Рис. 5.7. Варианты расположения зубчатых колес в группе передач: а – в случае выполнения только одного из условий (5.3); б – в случае выполнения обоих условий (5.3)

Если условия (5.4) не выполняются или выполняются не полностью, то зубчатые колеса этой группы передач можно расположить согласно схемам, изображенным на рис. 5.7. При варианте (а) увеличиваются осевые габариты, а при варианте (б) усложняется механизм переключения скоростей, и целью обеспечения свободного нейтрального положения блоку колес необходимо, чтобы расстояние «В» между неподвижно закрепленными колесами было на 4...6 мм больше размера «Д» (см. рис. 5.7, а). Это требование необходимо соблюдать и при вычерчивании кинематической схемы приводов.

ПРЕДВАРИТЕЛЬНЫЙ ПРОЧНОСТНОЙ РАСЧЕТ ПРИВОДА

После того как построен график частот вращения шпинделя, вычерчена кинематическая схема коробки скоростей и определены числа зубьев колес, переходим к прочностному расчету привода, который выполняется в такой последовательности.

1. Определение расчетной частоты вращения шпинделя

Расчетную частоту вращения шпинделя определяем по формуле

где nmin иnmax– соответственно минимальная и максимальная частоты вращения шпинделя по геометрическому ряду. В нашем примере