Целые и рациональные числа. Действительные числа.

Число — важнейшее математическое понятие, меняющееся на протяжении веков.

Первые представления о числе возникли из счета людей, животных, плодов, различных изделий и пр. Результатом являются натуральные числа: 1, 2, 3, 4, ...

Исторически первым расширением понятия числа является присоединение к натуральному числу дробных чисел.

Дробью называется часть (доля) единицы или несколько равных ее частей.

Обозначаются: 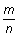, где m, n— целые числа;

Дроби со знаменателем 10n, где n— целое число, называются десятичными:  .

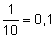Среди десятичных дробей особое место занимают периодические дроби: 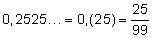— чистая периодическая дробь, — смешанная периодическая дробь.

Дальнейшее расширение понятия числа вызвано уже развитием самой математики (алгебры). Декарт в XVII в. вводит понятие отрицательного числа.

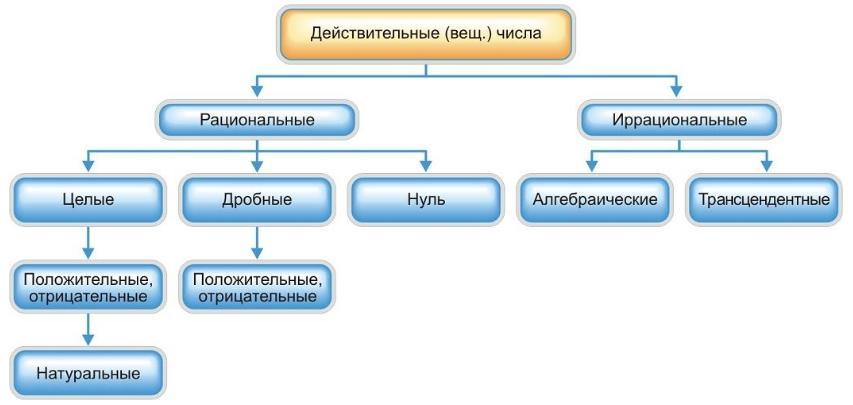
Числа целые (положительные и отрицательные), дробные (положительные и отрицательные) и нуль получили название рациональных чисел. Всякое рациональное число может быть записано в виде дроби конечной и периодической.

Для изучения непрерывно изменяющихся переменных величин оказалось необходимым новое расширение понятия числа — введение действительных (вещественных) чисел — присоединением к рациональным числам иррациональных: иррациональные числа — это бесконечные десятичные непериодические дроби.

Иррациональные числа появились при измерении несоизмеримых отрезков (сторона и диагональ квадрата), в алгебре — при извлечении корней , примером трансцендентного, иррационального числа являются π, e .

Числа натуральные (1, 2, 3,...), целые (..., –3, –2, –1, 0, 1, 2, 3,...), рациональные (представимые в виде дроби) и иррациональные (не представимые в виде дроби) образуют множество действительных (вещественных) чисел.

Отдельно в математике выделяют комплексные числа.

Комплексные числа возникают в связи с задачей решения квадратных для случая D < 0 ( здесь D – дискриминант квадратного уравнения). Долгое время эти числа не находили физического применения, поэтому их и назвали «мнимыми» числами. Однако сейчас они очень широко применяются в различных областях физики и техники: электротехнике, гидро- и аэродинамике, теории упругости и др.

Комплексные числа записываются в виде: z=a+ bi. Здесь a и b – действительные числа, а i – мнимая единица, т.e. i ² = –1. Число a называется абсциссой, a b – ординатой комплексного числа a+ bi. Два комплексных числа a+ bi и a – bi называются сопряжёнными комплексными числами.

Свойства:

1. Действительное число а может быть также записано в форме комплексного числа: a+ 0i или a – 0i. Например 5 + 0i и 5 – 0i означают одно и то же число 5 .

2. Комплексное число 0+ bi называется чисто мнимым числом. Запись bi означает то же самое, что и 0+ bi.

3. Два комплексных числа a+ bi и c+ di считаются равными, если a= c и b= d. В противном случае комплексные числа не равны.

Действия:

Сложение. Суммой комплексных чисел a+ bi и c+ di называется комплексное число (a+ c) + (b+ d)i. Таким образом, при сложении комплексных чисел отдельно складываются их абсциссы и ординаты.

Вычитание. Разностью двух комплексных чисел a+ bi (уменьшаемое) и c+ di (вычитаемое) называется комплексное число (a – c) + (b – d)i.Таким образом, при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.

Умножение. Произведением комплексных чисел a+ bi и c+ di называется комплексное число:

(ac – bd) + (ad + bc)i . Это определение вытекает из двух требований:

1) числа a+ bi и c+ di должны перемножаться, как алгебраические двучлены,

2) число i обладает основным свойством:  i ² = –1.

П р и м е р .  ( a+ bi )( a – bi )= a ² + b ². Следовательно, произведение двух сопряжённых комплексных чисел равно действительному положительному числу.

Деление. Разделить комплексное число  a+ bi (делимое) на другое c+ di (делитель) - значит найти третье число e+ f i (чатное), которое будучи умноженным на делитель c+ di,  даёт в результате делимое  a+ bi. Если делитель не равен нулю, деление всегда возможно.

П р и м е р .  Найти  ( 8 + i ) : ( 2 – 3i ) .

Р е ш е н и е . Перепишем это отношение в виде дроби: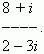

Умножив её числитель и знаменатель на  2 + 3i и выполнив все преобразования, получим:

 

 

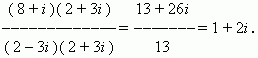
Задание 1: Сложите, вычтите, умножьте и разделите z₁ на z₂

1) ,

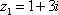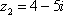
2) ,

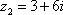
3) ,

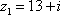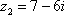
Извлечение корня квадратного: Реши уравнение x ² = -a. Для решения данного уравнения мы вынуждены воспользоваться числами нового типа – мнимые числа. Таким образом,  мнимым называется число, вторая степень которого является числом отрицательным. Согласно этому определению мнимых чисел мы можем определить и мнимую единицу:

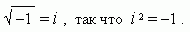
Тогда для уравнения  x ² = – 25  мы получаем два мнимых корня:

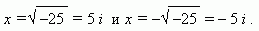
Задание 2: Реши уравнение:

1) x ² = – 36; 2) x ² = – 49; 3) x ² = – 121

Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой:

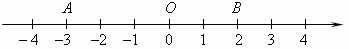
Здесь точка Aозначает число –3, точка B–число 2, и  O –ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ bi будет представлено точкой  Р  с абсциссой а и ординатой b. Эта система координат называется комплексной плоскостью.

Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа  a+ bi обозначается  | a+ bi | или ) буквой  r  и равен:

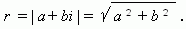
Сопряжённые комплексные числа имеют одинаковый модуль.

Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат По осям нужно задать размерность, отмечаем:

ноль;

е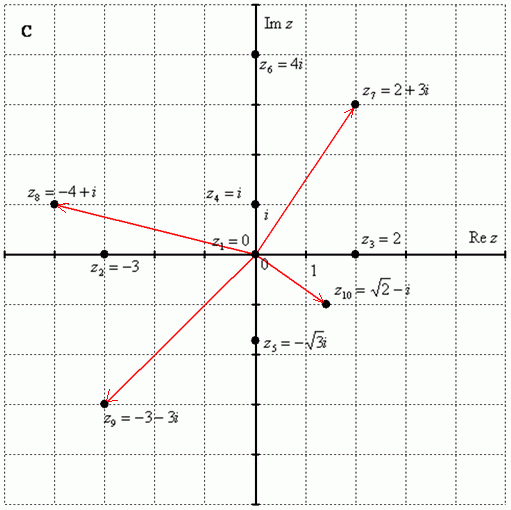диницу по действительной оси; Re_z

мнимую единицу по мнимой оси. Im_z

Задание 3. Построить на комплексной плоскости следующие комплексные числа: , , , , , , ,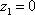

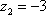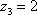
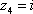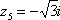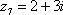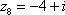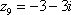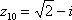
1. Числа точные и приближенные. Числа, с которыми мы встречаемся на практике, бывают двух родов. Одни дают истинное значение величины, другие - только приблизительное. Первые называют точными, вторые - приближенными. Чаще всего удобно пользоваться приближенным числом вместо точного, тем более, что во многих случаях точное число вообще найти невозможно.

Так, если говорят, что в классе есть 29 учеников, то число 29 - точное. Если же говорят, что расстояние от Москвы до Киева равно 960 км, то здесь число 960 - приближенное, так как, с одной стороны, наши измерительные инструменты не абсолютно точны, с другой стороны, сами города имеют некоторую протяженность.

Результат действий с приближенными числами есть тоже приближенное число. Выполняя некоторые действия над точными числами (деление, извлечение корня), можно также получить приближенные числа.

Теория приближенных вычислений позволяет:

1) зная степень точности данных, оценить степень точности результатов;

2) брать данные с надлежащей степенью точности, достаточной для обеспечения требуемой точности результата;

3) рационализировать процесс вычисления, освободив его от тех выкладок, которые не окажут влияния на точность результата.

2. Округление. Одним из источников получения приближенных чисел является округление. Округляют как приближенные, так и точные числа.

Округлением данного числа до некоторого его разряда называют замену его новым числом, которое получается из данного путем отбрасывания всех его цифр, записанных правее цифры этого разряда, или путем замены их нулями. Эти нули обычно подчеркивают или пишут их меньшими. Для обеспечения наибольшей близости округленного числа к округляемому следует пользоваться такими правилами: чтобы округлить число до единицы определенного разряда, надо отбросить все цифры, стоящие после цифры этого разряда, а в целом числе заменить их нулями. При этом учитывают следующее:

1) если первая (слева) из отбрасываемых цифр менее 5, то последнюю оставленную цифру не изменяют (округление с недостатком);

2) если первая отбрасываемая цифра больше 5 или равна 5, то последнюю оставленную цифру увеличивают на единицу (округление с избытком).

Покажем это на примерах. Округлить:

а) до десятых 12,34;

б) до сотых 3,2465; 1038,785;

в) до тысячных 3,4335.

г) до тысяч 12375; 320729.

Ответы.

а) 12,34 ≈ 12,3;

б) 3,2465 ≈ 3,25; 1038,785 ≈ 1038,79;

в) 3,4335 ≈ 3,434.

г) 12375 ≈ 12 000; 320729 ≈ 321000.

3. Абсолютная и относительная погрешности. Разность между точным числом и его приближенным значением называется абсолютной погрешностью приближенного числа. Например, если точное число 1,214 округлить до десятых, получим приближенное число 1,2. В данном случае абсолютная погрешность приближенного числа 1,2 равна 1,214 - 1,2, т.е. 0,014.

Но в большинстве случаев точное значение рассматриваемой величины неизвестно, а только приближенное. Тогда и абсолютная погрешность неизвестна. В этих случаях указывают границу, которую она не превышает. Это число называют граничной абсолютной погрешностью. Говорят, что точное значение числа равно его приближенному значению с погрешностью меньшей, чем граничная погрешность. Например, число 23,71 есть приближенное значение числа 23,7125 с точностью до 0,01, так как абсолютная погрешность приближения равна 0,0025 и меньше 0,01. Здесь граничная абсолютная погрешность равна 0,01^*.

Граничную абсолютную погрешность приближенного числа а обозначают символом Δa . Запись

x ≈a (±Δa )

следует понимать так: точное значение величины x находится в промежутке между числамиа – Δa иа + Δа , которые называют соответственно нижней и верхней границейх и обозначают НГx ВГх .

Например, если x ≈ 2,3 (±0,1), то 2,2<x < 2,4.

Наоборот, если 7,3< х < 7,4, тох ≈ 7,35 (±0,05). Абсолютная или граничная абсолютная погрешность не характеризует качество выполненного измерения. Одна и та же абсолютная погрешность может считаться значительной и незначительной в зависимости от числа, которым выражается измеряемая величина. Например если измеряем расстояние между двумя городами с точностью до одного километра, то такая точность вполне достаточна для этого изменения в то же время при измерении расстояния между двумя домами одной улицы такая точность будет недопустимой. Следовательно, точность приближенного значения величины зависит не только от величины абсолютной погрешности, но и от значения измеряемой величины. Поэтому мерой точности служит относительная погрешность.

Относительной погрешностью называется отношение абсолютной погрешности к величине приближенного числа. Отношение граничной абсолютной погрешности к приближенному числу называют граничной относительной погрешностью; обозначают ее так: . Относительную и граничную относительную погрешности принято выражать в процентах. Например, если измерения показали, что расстояниех между двумя пунктами больше 12,3 км, но меньше 12,7 км, то за приближенное значение его принимают среднее арифметическое этих двух чисел, т.е. их полусумму, тогда граничная абсолютная погрешность равна полуразности этих чисел. В данном случаех ≈ 12,5 (±0,2). Здесь граничная абсолютная погрешность равна 0,2 км, а граничная относительная

.