
Задачи по туризму
.docЗадача 1. Группа туристов за два дня прошла 72км. При этом расстояния, пройденные первый и второй дни, относятся как 3: 5. Сколько км прошли туристы в первый и второй дни?
Решение:
-
3+5= 8 – всего частей.
-
72:8 = 9 (км) – на одну часть.
-
3*9 =27 (км) – в первый день.
-
5*9 = 45 (км) – во второй день
Ответ: 27 км, 45 км.
Задача 2. В походе туристы могут провести два дня. Длина маршрута по карте составляет 78 км. В первый день они собираются идти 6 ч. а во второй - 7 ч. Сколько километров они будут проходить ежедневно если их движения будет одинаковым.
1 день - 6ч по ?км
2 день - 7 ч по ?км
Всего - 78 км
Решение:
1) 6 + 7 - 13 (ч) - время в пути
2) 78 : 13 = 6 (км) - продят в среднем за 1 час
3) 6*6 = 36 (км) - прошли за 1 день
4) 6*7 = 42 (км) - прошли за 2 день
Ответ: 36 км – за 1 день, 42 км – за 2 день.
Задача 3. Пусть три группы туристов расположены в пунктах А, В, С, не лежат на одной прямой. Для проведения общего костра турфирме надо выбрать место, равноудаленное от этих групп. Как это можно сделать?
Решение:
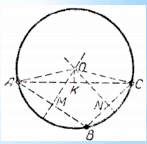
Соединим эти точки отрезками АВ и ВС. Чтобы найти точки равноудаленные от точек А и В проведем серединный перпендикуляр к АВ. Чтобы найти точки, равноудалённые от точек В и С, проведем серединный перпендикуляр к ВС. Точка О - точка пересечения этих перпедикуляров будет равноудалена от данных точек А, В и С. Точка О служит центром окружности, проходящей через точки А, В и С, не лежащие на одной прямой.
Ответ: Задача имеет единственное решение.
Значит в пункте О можно организовать общий костер для трёх групп.
Задача 4. Два туриста вышли одновременно навстречу друг другу и встретились через 2,5 часов. Скорость первого туриста равна 4,2 км/ч, а скорость второго - 5,2 км/ч. Какое расстояние было между туристами в начале движения?
Решение: 1) 4,2 * 2,5 = 10,5 (км) расстояние, которое прошёл 1-й пешеход
2) 5,2 * 2,5 = 13 (км) расстояние, которое прошёл 2-й пешеход
3) 10,5 + 13 = 23,5 (км) расстояние между туристами вначале движения
Ответ: 23,5 км расстояние между туристами вначале движения.
Задача 5. Турист проехал на поезде и на теплоходе 605 км. Средняя скорость поезда 60 км/ч, теплохода 25 км/ч. Сколько времени турист ехал на поезде, если известно, что на теплоходе он ехал на 3 часа меньше, чем на поезде?
Решение:
Нужно за х принять количество часов, которое он ехал на поезде.
Тогда количество часов, проведенных на теплоходе равно х - 3.
Составляем уравнение:
60х + 25(х-3) = 605
60х + 25х - 75 = 605
85х =605+75
85х = 680
х = 8 часов - время езды на поезде
Отсюда 8 - 3 = 5 часов - время, которое он плыл на теплоходе.
Ответ: 8 ч – езда на поезде.
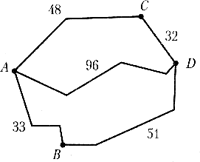
Задача 6. Группе туристов нужно попасть из А в пункт D эффективным путём. Из пункта A в пункт D ведут три дороги. Через пункт B едет грузовик со средней скоростью 42 км/ч, через пункт C едет автобус со средней скоростью 32 км/ч. Третья дорога без промежуточных пунктов, и по ней движется легковой автомобиль со средней скоростью 64 км/ч. На рисунке показана схема дорог и расстояние между пунктами по дорогам. Все три машины одновременно выехали из пункта A. Какая машина добралась до D раньше других? В ответе укажите, сколько часов она находилась в дороге.
Решение:
|
|
S (км) |
t (ч) |
|
Грузовик |
33 + 51 =84 |
84 : 42 = 2 |
|
Автобус |
48 + 32 = 80 |
80 : 32 = 2,5 |
|
Автомобиль |
96 |
96 : 64 = 1,5 |
Ответ: Автомобиль добрался до D раньше других. 1,5 часа он находился в дороге.
Задача 7. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Решение.
На первом рейсе
6 мест, всего мест 30. Тогда вероятность
того, что турист П. полетит
первым рейсом вертолёта, равна:
![]()
Ответ: 0,2.
Задача 8. В группе из 20 российских туристов несколько человек владеют иностранными языками. Из них пятеро говорят только по-английски, трое только по-французски, двое по-французски и по-английски. Какова вероятность того, что случайно выбранный турист говорит по-французски?
Решение.
Количество
туристов, говорящих
по-французски, равно 5. Поэтому
вероятность того, что случайно
выбранный турист говорит
по-французски равна
![]()
Ответ: 0,25
Задача 9. 9 туристов на удачу рассаживаются по 12 вагонам электрички. Найти вероятность того, что все они окажутся: 1)В одном вагоне 2)Во втором вагоне 3)В разных вагонах
Решение.
Используем теорему о вероятности произведения событий
а) (1/12)^8 б) (11/12)*(10/12)*(9/12)*(8/12)*(7/12)*(6/12)*(5/12)*(4/12)
Ответ: Р= 0,66666664
Задача 10. Имеется круглое глубокое озеро диаметром 200 метров и два дерева, одно из которых растет на берегу у самой воды, другое - по центру озера на небольшом островке. Человеку, который не умеет плавать, нужно перебраться на островок при помощи веревки, длина которой чуть больше 200 м. Как ему это сделать?
Решение: Нужно обойти вокруг озера и веревка зацепиться об дерево. И таким образом, человек с помощью веревки переберется на островок.
