8. Эмпирические центральные и начальные моменты

Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия о моментах вариационного ряда.

Эмпирическим начальным моментом () порядка q называют взвешенную среднюю арифметическую q-x степеней вариантов, т.е.

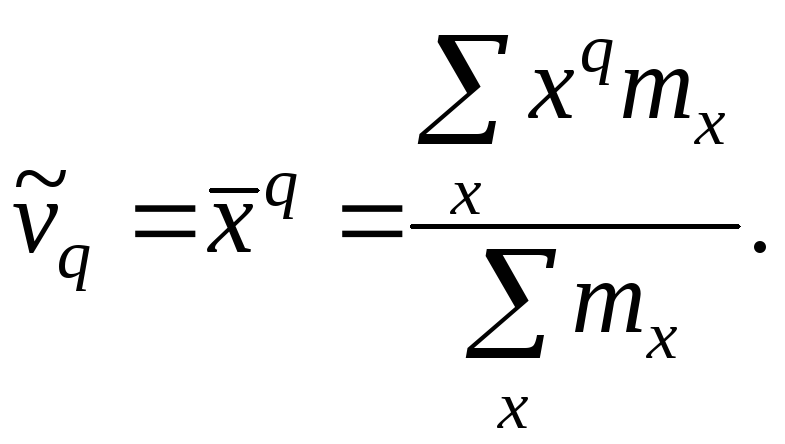(20)

Эмпирический начальный момент нулевого порядка

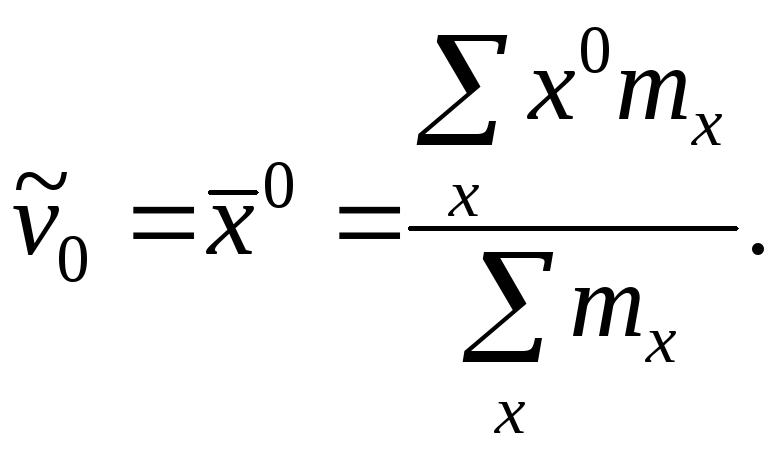
Эмпирический начальный момент первого порядка

Эмпирический начальный момент второго порядка 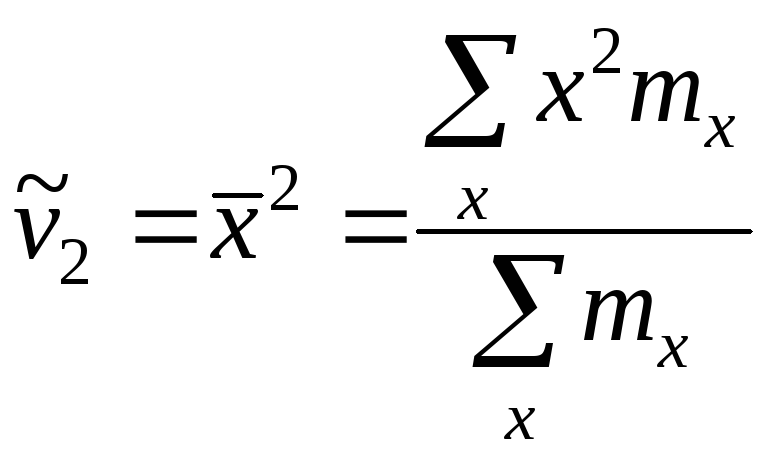и т.д.

Эмпирическим центральным моментом () порядкаq называют взвешенную среднюю арифметическую q-x степеней отклонений вариантов от их средней арифметической, т.е.

(21)

Эмпирический центральный момент нулевого порядка

Эмпирический центральный момент первого порядка

(в силу свойства 1° средней арифметической).

Эмпирический центральный момент второго порядка

В дальнейшем для краткости величину часто будем называть просто центральным моментом (начальным моментом), не употребляя термин «эмпирический».

Используя формулу бинома Ньютона, разложим в ряд выражение для центрального момента q-го порядка:

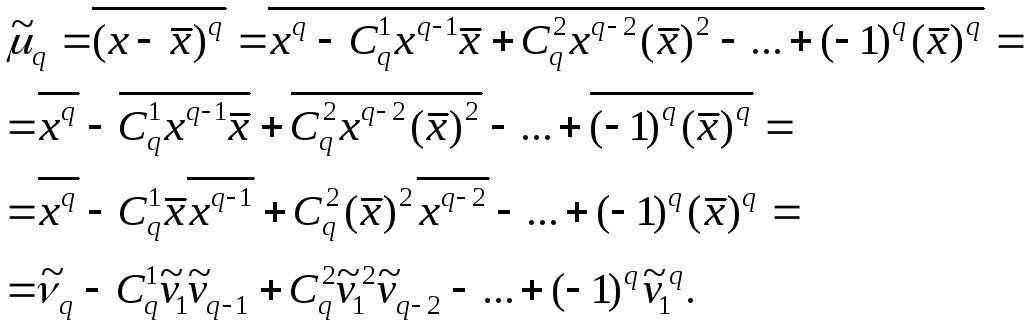
В проведенных тождественных преобразованиях использованы свойства 5° и 3° средней арифметической; — число сочетаний из q элементов по р элементов (p≤.q).

Итак, центральный момент q-го порядка выражается через начальные моменты следующим образом:

(22)

Полагая q = 0, 1, 2,…, можно получить выражения центральных моментов различных порядков через начальные моменты:

;

₍₂₃₎

₍₂₄₎

₍₂₅₎

и т.д.

Заметим, что формула (23) для центрального момента второго порядка, как и следовало ожидать, аналогична формуле (18) для дисперсии.

Рассмотрим свойства центральных моментов, которые позволят значительно упростить их вычисление.

1°. Если все варианты уменьшить (увеличить) на одно и то же число с, то центральный момент q-го порядка не изменится.

Доказательство. Если все варианты уменьшить на число с, то средняя арифметическая для измененного ряда равна -с, поэтому центральный момент q-го порядка

Аналогично можно показать, что

2°. Если все варианты уменьшить (увеличить) в одно и то же число k раз, то центральный момент q-го порядка уменьшится (увеличится) в раз.

Доказательство. Если все варианты уменьшить в одно и то же число k раз, то средняя арифметическая для измененного вариационного ряда равна , поэтому центральный момент q-гo порядка

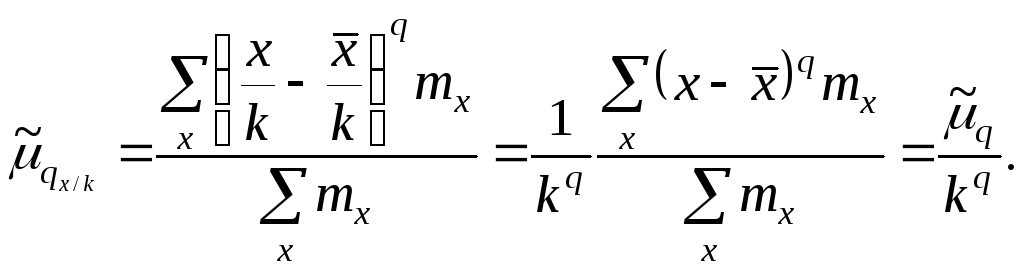
Аналогично можно показать, что

Для облегчения расчётов центральные моменты вычисляют не по первоначальным вариантам х, а по вариантам х'=(х — с)/k. Зная (центральный момент q-го порядка для измененного ряда), легко вычислить центральный момент q-го порядка для первоначального ряда:

(26)

Действительно, принимая во внимание свойства центрального момента, получаем

откуда следует, что

9. Эмпирические асимметрия и эксцесс

Эмпирическим коэффициентом асимметрии называют отношение центрального момента третьего порядка к кубу среднеквадратического отклонения:

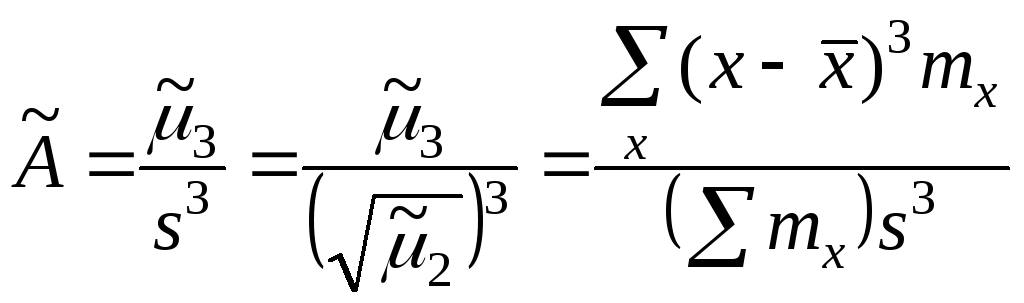. (27)

Если полигон вариационного ряда скошен, т.е. одна из его ветвей, начиная от вершины, зримо длиннее другой, то такой ряд называют асимметричным. Из формулы (27) следует, что если в вариационном ряду преобладают варианты, меньшие , то эмпирический коэффициент асимметрии отрицателен; говорят, что в этом случае имеет место левосторонняя асимметрия. Если же в вариационном ряду преобладают варианты, большие , то эмпирический коэффициент асимметрии положителен; в этом случае имеет место правосторонняя асимметрия. При левосторонней асимметрии левая ветвь полигона длиннее правой. При правосторонней, более длинной является правая ветвь.

Эмпирический коэффициент асимметрии не имеет ни верхней, ни нижней границы, что снижает его ценность как меры асимметрии. Практически коэффициент асимметрии редко бывает особенно велик, а для умеренно асимметричных рядов он обычно меньше единицы.

Эмпирическим эксцессом или коэффициентом крутости называют уменьшенное на 3 единицы отношение центрального момента четвертого порядка к четвертой степени среднеквадратического отклонения:

. (28)

За стандартное значение эксцесса принимают нуль-эксцесс так называемой нормальной кривой (см. рис. 1).

Кривые, у которых эксцесс отрицательный, по сравнению с нормальной менее крутые, имеют, более плоскую вершину и называются «плосковершинными» Кривые с положительным эксцессом более крутые по сравнению с нормальной кривой, имеют более острую вершину и называются «островершинными».

Заключение по лекции:

В лекции мы рассмотрели характеристики вариационного ряда. В ходе подготовки к последующей лекции и практическим занятиям вы должны самостоятельно при углубленном изучении рекомендованной литературы и решения предложенных задач дополнить свои конспекты лекций.

Приложения