5. Медиана и мода

Наряду со средними величинами в качестве описательных характеристик вариационного ряда применяют медиану и моду.

Медианой () называют значение признака, приходящееся на середину ранжированного ряда наблюдений.

Пусть проведено нечётное число наблюдений, т.е. n=2q—1, и результаты наблюдений проранжированы и выписаны в следующий ряд: Здесь— значение признака, занявшееi-e порядковое место в ранжированном ряду. На середину ряда приходится значение Следовательно,

=

Если проведено чётное число наблюдений, т.е. п=2q, то на середину ранжированного ряда приходятся значения и. В этом случае за медиану принимают среднюю арифметическую значенийи_{, т.е.}

Покажем на примерах на практическом занятии, как определяется медиана дискретного и интервального вариационных рядов.

В общем случае медиана для интервального вариационного ряда определяется по формуле

(9)

или по следующей формуле, полученной из формулы (9) в результате деления числителя и знаменателя входящей в неё дроби на п:

, (10)

где а_е — начало медианного интервала, т.е. такого, которому соответствует первая из накопленных частот (накопленных частостей), равная или большая половине всех наблюдений (≥0,5); () —частота (частость), накопленная к началу медианного интервала; (w_e)—частота (частость) медианного интервала.

Модой () называют такое значение признака, которое наблюдалось наибольшее число раз. Нахождение моды для дискретного вариационного ряда не требует каких-либо вычислений, так как ею является вариант, которому соответствует наибольшая частота.

В случае интервального вариационного ряда мода вычисляется по следующей формуле (вывод формулы можно найти в кн.: Венецкий И. Г., Кильдишев Г. С. Теория вероятностей и математическая статистика. М., 1975.):

(11)

или по тождественной формуле:

(12)

где — начало модального интервала, т.е. такого, которому соответствует наибольшая частота (частость); (w₀) — частота (частость) модального интервала; ) — частота (частость) интервала, предшествующего модальному; (w"₀) — частота (частость) интервала, следующего за модальным.

Моду используют в случаях, когда нужно ответить на вопрос, какой товар имеет наибольший спрос, каковы преобладающие в данный момент уровни производительности труда, себестоимости и т. д. Модальная производительность, себестоимость и т.д. помогают вскрыть ресурсы, имеющиеся в экономике.

6. Показатели вариации

Средние величины, характеризуя вариационный ряд числом, не отражают изменчивости наблюдавшихся значений признака, т.е. вариацию. Простейшим показателем вариации является вариационный размах (R_B), равный разности между наибольшим и наименьшим вариантами, т.е.

(13)

Вариационный размах — приближённый показатель вариации, так как почти не зависит от изменения вариантов, а крайние варианты, которые используются для его вычисления, как правило, ненадёжны.

Более содержательными являются меры рассеяния наблюдений вокруг средних величин. Средняя арифметическая является основным видом средних, поэтому ограничимся рассмотрением мер рассеяния наблюдений вокруг средней арифметической.

Сумма отклонений результатов наблюдений от средней арифметической , т.е. не может характеризовать вариацию наблюдений около средней арифметической. В силу свойства 1° эта сумма равна нулю. Берут или абсолютные величины, или квадраты разностей В результате получают различные показатели вариации.

Средним линейным отклонением (d) называют среднюю арифметическую абсолютных величин отклонений результатов наблюдений от их средней арифметической:

(14)

Эмпирической дисперсией (s²) называют среднюю арифметическую квадратов отклонений результатов наблюдений от их средней арифметической:

₍₁₅₎

Если по результатам наблюдений построен вариационный ряд, то эмпирическая дисперсия

(16)

Вместо эмпирической дисперсии в качестве меры рассеяния наблюдений вокруг средней арифметической часто используют эмпирическое среднеквадратическое отклонение, равное арифметическому значению корня квадратного из дисперсии и имеющее ту же размерность, что и значения признака.

Для вариационного ряда среднеквадратическое отклонение

(17)

где х — вариант (если ряд дискретный) и центр интервала (если ряд интервальный); m_x(w_x) — соответствующая частота (частость); — средняя арифметическая.

Для краткости величину s² часто будем называть просто дисперсией, не употребляя термина «эмпирическая». Однако при этом всегда следует помнить, что в этом случае дисперсия вычислена по результатам наблюдений на основании опытных данных, т.е. является эмпирической. Аналогичное замечание относится и к величине s.

Приведем свойство минимальности эмпирической дисперсии: s² меньше взвешенной средней арифметической квадратов отклонений вариантов от любой постоянной величины, отличной от средней арифметической, т.е.

если

Доказательство. Найдём экстремум функции f(a)= . Для этого решим уравнение f'(a) =0. Имеем:

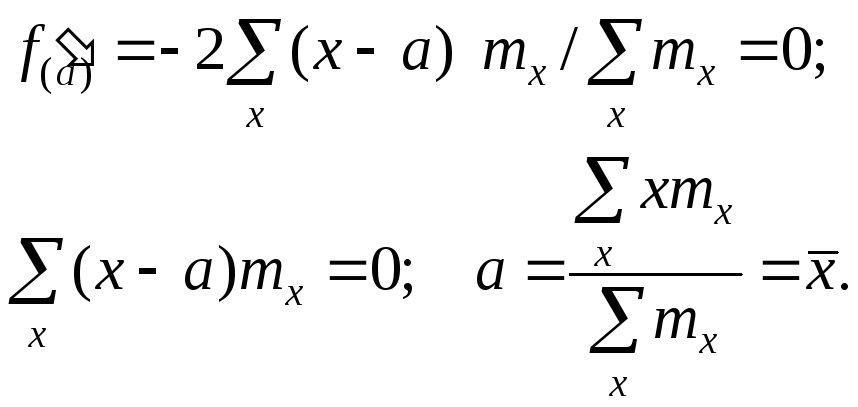
Так как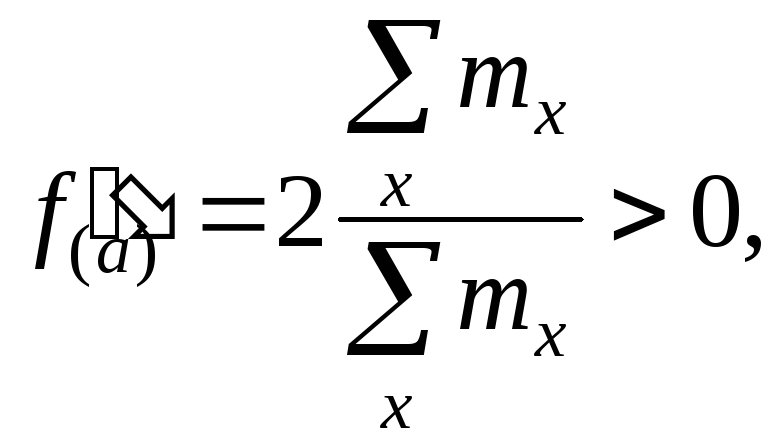то функция f(a) имеет в точке а= минимум.

Можно показать, что среднее линейное отклонение не обладает свойством минимальности. Поэтому наиболее употребительными мерами рассеяния наблюдений вокруг средней арифметической являются эмпирическая дисперсия и эмпирическое среднеквадратическое отклонение.

Итальянский статистик Коррадо Джинни предложил в качестве показателя вариации использовать величину

где — ряд наблюдений. Особенность этого показателя состоит в том, что он зависит только от разностей между наблюдениями и измеряет как бы «внутреннюю изменчивость» значений признака, а не их рассеяние вокруг какой-либо точки. Можно показать, что , т. е.s², являясь мерой рассеяния значений признака вокруг средней арифметической, характеризует также и внутреннюю их изменчивость.