
Математика_2013_080200_оч_полн_1_сем_зач
.docx-:
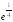
+:

-:

-:

I:
S: Предел функции
 равен
...
равен
...
-:
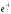
+:
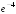
-:
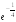
-:
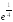
-:

V2: Непрерывность функции, точки разрыва. Асимптоты графика функции
I:
S: Количество точек разрыва
функции
 равно …
равно …
-: 3
-: 2
+: 1
-: 0
I:
S: Количество точек разрыва
функции
 равно …
равно …
+: 3
-: 2
-: 1
-: 0
I:
S: Функция
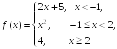 имеет
разрыв в точке x= …
имеет
разрыв в точке x= …
+: – 1
-: 2
-: 1
-: 3
I:
S: Функция
 имеет
разрыв в точке x= …
имеет
разрыв в точке x= …
-: – 1
+: 2
-: 1
-: 3
I:
S: Точками
разрыва функции
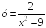 являются точки
являются точки

-: 0
-: 1
+: 3
+: –3
I:
S: Точками
разрыва функции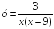 являются точки
являются точки

-: 4
+: 0
+: 9
-: -9
I:
S: Точками
разрыва функции
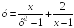 являются точки
являются точки

+: 1
-: 0
-: –2
+: –1
I:
S: Точками
разрыва функции
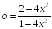 являются точки
являются точки

-: –2
+:

-: 2
+:

I:
S: Точками
разрыва функции
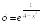 являются точки
являются точки

-: –1
+: 2
+: –2
-: 0
I:
S: Точками
разрыва функции
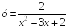 являются точки
являются точки

+: 1
-: 0
+: 2
-: 3
I:
I:
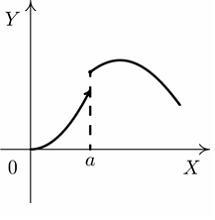
S: Установите
соответствие между графиком функции и
характером точки
![]() .
.
L1:

L2:
L3:

L4:
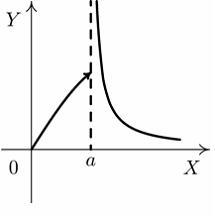
R2: точка разрыва 1-го рода
R3: точка устранимого разрыва
R1: точка непрерывности
R4: точка разрыва 2-го рода
R5: точка перегиба
I:
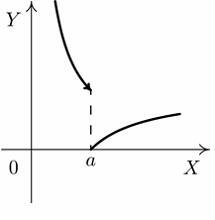
S: Установите
соответствие между графиком функции и
характером точки
![]() .
.
L1:

L2:
L3: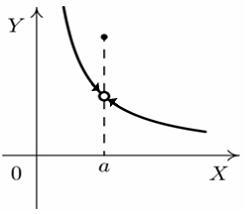
L4: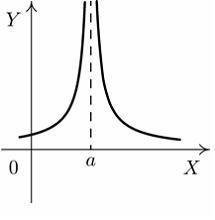
R3: точка устранимого разрыва
R5: точка максимума
R1: точка непрерывности
R2: точка разрыва 1-го рода
R4: точка разрыва 2-го рода
I:
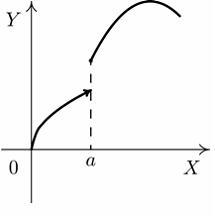
S: Установите
соответствие между графиком функции и
характером точки
![]()
L1:

L2:
L3:

L4:

R5: точка перегиба
R2: точка разрыва 1-го рода
R1: точка непрерывности
R3: точка устранимого разрыва
R4: точка разрыва 2-го рода
I:
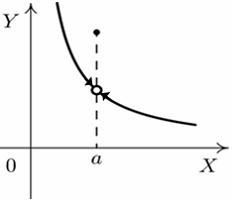
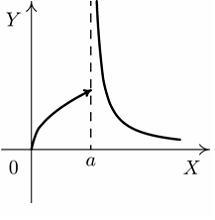
S: Установите
соответствие между графиком функции и
характером точки
![]() .
.
L1:

L2:

L3:
L4:
R3: точка устранимого разрыва
R4: точка разрыва 2-го рода
R2: точка разрыва 1-го рода
R5: точка перегиба
R1: точка непрерывности
I:
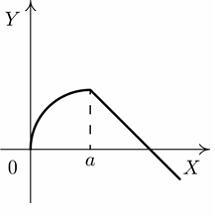
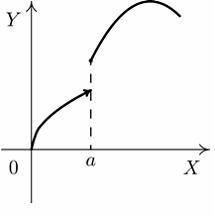
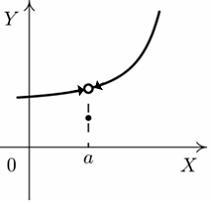
S: Установите
соответствие между графиком функции и
характером точки
![]() .
.
L1:
L2:
L3:
L4:
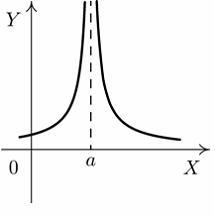
R1: точка непрерывности
R2: точка разрыва 1-го рода
R3: точка устранимого разрыва
R4: точка разрыва 2-го рода
R5: точка минимума
I:
S: Число точек
разрыва функции, заданной на отрезке
![]() ,
график которой имеет вид
,
график которой имеет вид
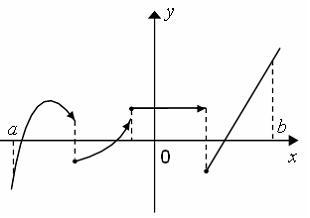
равно …
+: 3
I:
S: Число точек
разрыва функции, заданной на отрезке
![]() ,
график которой имеет вид
,
график которой имеет вид
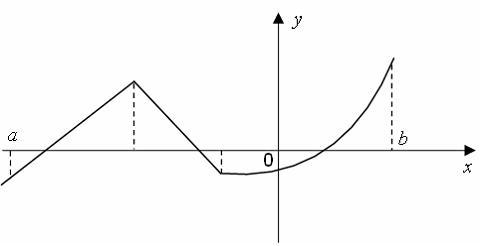
равно …
+: 0
I:
S: Число точек
разрыва функции, заданной на отрезке
![]() ,
график которой имеет вид
,
график которой имеет вид

равно …
+: 3
I:
S: Число точек
разрыва функции, заданной на отрезке
![]() ,
график которой имеет вид
,
график которой имеет вид

равно …
+: 5
I:
S: Число точек
разрыва функции, заданной на отрезке
![]() ,
график которой имеет вид
,
график которой имеет вид
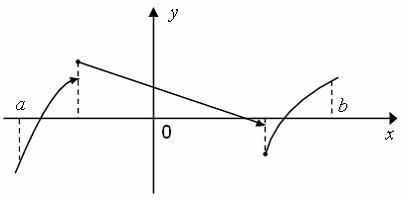
равно …
+: 2
I:
S: Уравнение
вертикальной асимптоты графика функции
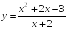 имеет
вид …
имеет
вид …
-:

-:

-:
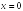
+:
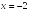
I:
S: Уравнение
вертикальной асимптоты графика функции
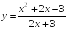 имеет
вид …
имеет
вид …
-:

+:

-:
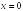
-:

I:
S: Уравнение
вертикальной асимптоты графика функции
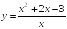 имеет
вид …
имеет
вид …
-:
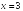
-:

+:

-:
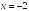
I:
S: Уравнение
вертикальной асимптоты графика функции
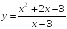 имеет
вид …
имеет
вид …
+:
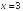
-:

-:
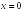
-:

I:
S: Уравнение
вертикальной асимптоты графика функции
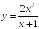 имеет
вид …
имеет
вид …
+:
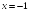
-:

-:

-:
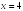
I:
S: Уравнение
вертикальной асимптоты графика функции
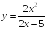 имеет
вид …
имеет
вид …
-:
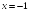
+:

-:
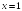
-:

I:
S: Уравнение
вертикальной асимптоты графика функции
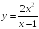 имеет
вид …
имеет
вид …
-:

-:

+:
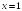
-:

I:
S: Уравнение
вертикальной асимптоты графика функции
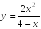 имеет
вид …
имеет
вид …
-:
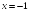
-:

-:
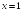
+:
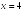
I:
S: График функции
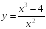 имеет следующие асимптоты
имеет следующие асимптоты
+:
Вертикальную
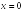
-:
Наклонную

-:
Горизонтальную
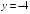
-:
Вертикальную
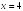
+:
Наклонную
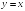
I:
S: График функции
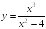 имеет следующие асимптоты
имеет следующие асимптоты
+:
Вертикальную

-:
Наклонную

-:
Горизонтальную
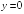
+:
Вертикальную
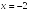
+:
Наклонную

I:
S: График функции
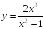 имеет следующие асимптоты
имеет следующие асимптоты
+:
Вертикальную
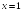
+:
Наклонную

-:
Горизонтальную
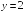
+:
Вертикальную

-:
Наклонную

I:
S: График функции
 имеет следующие асимптоты
имеет следующие асимптоты
+:
Вертикальную
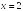
+:
Наклонную
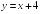
-:
Горизонтальную
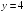
-:
Вертикальную
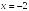
-:
Наклонную
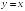
I:
S: График функции
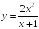 имеет следующие асимптоты
имеет следующие асимптоты
-:
Вертикальную
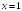
-:
Наклонную
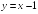
-:
Горизонтальную
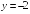
+:
Вертикальную

+:
Наклонную

I:
S: График функции
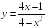 имеет следующие асимптоты
имеет следующие асимптоты
+:
Вертикальную

-:
Наклонную
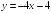
+:
Горизонтальную
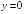
+:
Вертикальную

-:
Наклонную
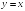
I:
S: График функции
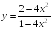 имеет следующие асимптоты
имеет следующие асимптоты
+:
Вертикальную
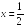
-:
Вертикальную

+:
Горизонтальную
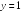
+:
Вертикальную
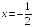
-:
Наклонную
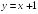
I:
S: График функции
 имеет следующие асимптоты
имеет следующие асимптоты
+:
Вертикальную

+:
Наклонную

-:
Горизонтальную
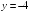
+:
Вертикальную
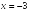
-:
Наклонную
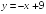
I:
S: График функции
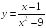 имеет следующие асимптоты
имеет следующие асимптоты
+:
Вертикальную
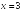
-:
Наклонную

+:
Горизонтальную
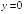
+:
Вертикальную
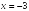
-:
Наклонную

I:
S: График функции
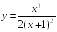 имеет следующие асимптоты
имеет следующие асимптоты
+:
Вертикальную

+:
Наклонную

-:
Горизонтальную
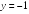
-:
Вертикальную
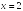
-:
Наклонную
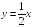
V1: Дифференциальное исчисление функций одной переменной
V2: Производные первого порядка
I:
S: Производная
функции
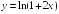 в точке
в точке
 равна
...
равна
...
+: 2/3
I:
S: Производная
функции
 в точке
в точке
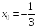 равна
...
равна
...
+: -1
I:
S: Производная
функции
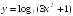 в точке
в точке
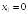 равна
...
равна
...
+: 0
I:
S: Производная
функции
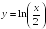 в точке
в точке
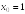 равна
...
равна
...
+: 1
I:
S: Производная
функции
 в точке
в точке
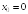 равна
...
равна
...
+: 0
I:
S: Производная
функции
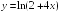 в точке
в точке
 равна
...
равна
...
+: 2
I:
S: Производная
функции
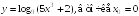 равна
...
равна
...
+: 0
I:
S: Производная
функции
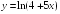 в точке
в точке
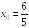 равна
...
равна
...
+: 1/2
I:
S: Производная
функции
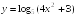 в точке
в точке
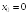 равна
...
равна
...
+: 0
I:
S: Производная
функции
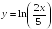 в точке
в точке
 равна
...
равна
...
+: 1
I:
S: Производная
функции
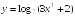 в точке
в точке
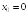 равна
...
равна
...
+: 0
I:
S: Производная
функции
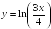 в точке
в точке
 равна
...
равна
...
+: 1
I:
S: Производная
функции
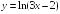 в точке
в точке
 равна
...
равна
...
+: 3
I:
S: Производная
функции
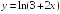 в точке
в точке
 равна
...
равна
...
+: 2
I:
S: Производная
функции
 в точке
в точке
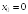 равна
...
равна
...
+: 0
I:
S: Производная
функции
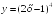 в точке
в точке

+: 8
I:
S: Производная
функции
 в точке
в точке
 равна
...
равна
...
+: 15
I:
S: Производная
функции
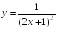 в точке
в точке
 равна
...
равна
...
+: 4
I:
S: Производная
функции
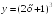 в точке
в точке
 равна
...
равна
...
+: 6
I:
S: Производная
функции
 в точке
в точке
 равна
...
равна
...
+: -12
I:
S: Производная
функции
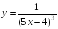 в точке
в точке
 равна
...
равна
...
+: -15
I:
S: Производная
функции
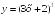 в точке
в точке
 равна
...
равна
...
+: 9
I:
S: Производная
функции
 в точке
в точке
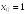 равна
...
равна
...
+: 8
I:
S: Производная
функции
 в точке
в точке
 равна
...
равна
...
+: -9
I:
S: Производная
функции
 в точке
в точке
 равна
...
равна
...
+: 4
I:
S: Производная
функции
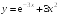 в точке
в точке
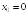 равна
...
равна
...
+: -3
I:
S: Производная
функции
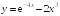 в точке
в точке
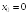 равна
...
равна
...
+: -4
I:
S: Производная
функции
 в точке
в точке
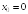 равна
...
равна
...
+: 1
I:
S: Производная
функции
 в точке
в точке
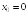 равна
...
равна
...
+: -9
I:
S: Производная
функции
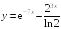
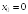 равна
...
равна
...
+: -10
I:
S: Материальная точка движется
прямолинейно по закону
 .
Тогда скорость точки в момент времени
.
Тогда скорость точки в момент времени
 равна …
равна …
-: 11
-: 18.5
+: 20
-: 19
I:
S: Закон движения
материальной точки имеет вид
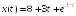 ,
где
,
где
 – координата точки в момент времени
– координата точки в момент времени
 .
Тогда скорость точки при
.
Тогда скорость точки при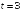 равна …
равна …
-: 10
-: 18
+: 2
-: 4
I:
S: Закон движения
материальной точки имеет вид
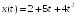 ,
где
,
где
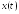 – координата точки в момент времени
– координата точки в момент времени
 .
Тогда скорость точки при
.
Тогда скорость точки при равна …
равна …
-: 15
-: 9
-: 11
+: 13
I:
S: Материальная
точка движется по закону
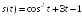 .
Тогда ее ускорение в момент времени
.
Тогда ее ускорение в момент времени
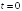 равно…
равно…
-: 2
-: 3
-: 0
+: –2
I:
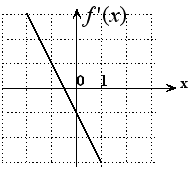
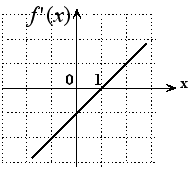
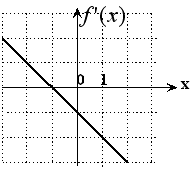
S: Дана функция
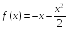 .
Графиком ее производной
.
Графиком ее производной
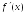 является
…
является
…
-:
-:

-:
+:
I:
S: График функции
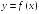 изображен
на рисунке.
изображен
на рисунке.

Тогда
значение производной этой функции в
точке
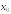 равно
….
равно
….
-:
![]()
-:
![]()
+:
![]()
-:
![]()
I:
S: График функции
 изображен
на рисунке.
изображен
на рисунке.
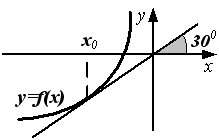
Тогда
значение производной этой функции в
точке
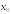 равно
….
равно
….
-:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S: График функции
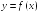 изображен
на рисунке.
изображен
на рисунке.
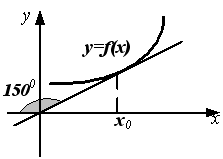
Тогда
значение производной этой функции в
точке
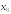 равно
….
равно
….
+:
![]()
-:
![]()
-:
![]()
-:
![]()
I:
S: График функции
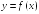 изображен
на рисунке.
изображен
на рисунке.

Тогда
значение производной этой функции в
точке
 равно
….
равно
….
-:
![]()
+:
![]()
-:
![]()
-:
![]()
I:
S: При любом
значении переменной
 для функции
для функции
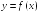 ,
изображенной на графике,
,
изображенной на графике,

верно равенство …
-:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S: Касательная
к графику функции
 не
пересекает прямую
не
пересекает прямую
 .
Тогда абсцисса точки касания равна …
.
Тогда абсцисса точки касания равна …
+: 2
-: –2
-: –4
-: 0
-:
![]()
I:
S: Угловой
коэффициент касательной, проведенной
к графику функции
![]() в
точке
в
точке
![]() ,
равен …
,
равен …
-: –2
-: 2
-: 3
+: 1
I:
S: Число
интервалов, на которых касательная к
графику функции
![]()

имеет отрицательный угловой коэффициент, равно …
-: 0
+: 1
-: 2
-: 3
I:
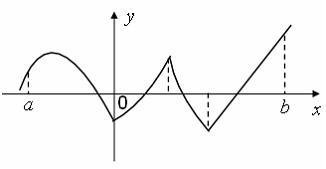
S: Количество
точек, принадлежащих интервалу
 ,
в которых не существует производная
функции, изображенной на рисунке,
,
в которых не существует производная
функции, изображенной на рисунке,

равно...
+: 4
I:
S: Количество
точек, принадлежащих интервалу
 ,
в которых не существует производная
функции, изображенной на рисунке,
,
в которых не существует производная
функции, изображенной на рисунке,
равно …
+: 3
I:
S: Количество
точек, принадлежащих интервалу
 ,
в которых не существует производная
функции, изображенной на рисунке,
,
в которых не существует производная
функции, изображенной на рисунке,

равно …
+: 2
I:
S: Количество
точек, принадлежащих интервалу
 ,
в которых не существует производная
функции, изображенной на рисунке,
,
в которых не существует производная
функции, изображенной на рисунке,
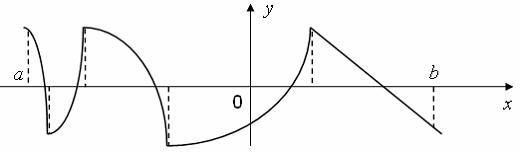
равно …
+: 4
V2: Производные сложной функции
I:
S: Производная
функции
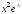 равна
…
равна
…
-:
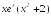
+:
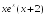
-:
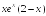
-:

I:
S: Производная
функции
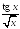 равна…
равна…
-:
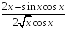
-:
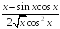
+:
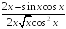
-:
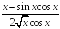
I:
S: Производная
функции
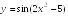 равна…
равна…
-:
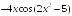
-:
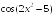
+:

-:

I:
S: Производная
функции
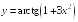 равна…
равна…
-:
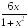
-:
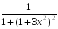
+:

-:

I:
S: Производная
функции
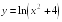 равна…
равна…
+:

-:
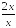
-:

-:

I:
S: Производная
функции
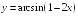 равна…
равна…
-:

-:
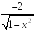
+:
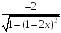
-:
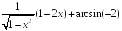
I:
S: Производная
функции
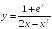 равна…
равна…
-:
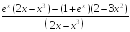
+:

-:
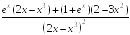
-:

V2: Производные высших порядков
I:
S: Производная
второго порядка функции
![]() равна …
равна …
-:
![]()
-:
![]()
-:
![]()
