
Математика_2013_080200_оч_полн_1_сем_зач
.docx
2: h
3: f
4: g
1: u
I:
S: Укажите последовательность этих прямых в порядке убывания их угловых коэффициентов.
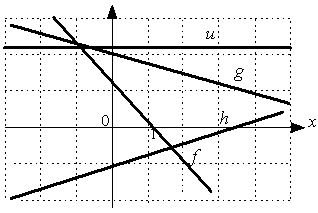
3: g
4: f
1: h
2: u
I:
S: Расстояние
от точки
 до прямой
до прямой
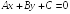 можно найти по формуле
можно найти по формуле
+:
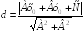
-:

-:
I:
S: Расстояние от точки
![]() до
прямой
до
прямой
![]() равно …
равно …
-:
![]()
+: 7
-:
![]()
-: 35
I:
S: Острый угол между прямыми
линиями ![]() и
и
![]() равен …
равен …
-:
![]()
+:
![]()
-:
![]()
-:
![]()
I:
S: Прямые
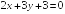 и
и
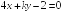 параллельны при
параллельны при
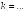
+: 6
I:
S: Прямые
 и
и
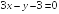 параллельны при
параллельны при
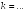
+: 6
I:
S: Прямые
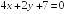 и
и
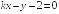 параллельны при
параллельны при
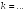
+: -2
I:
S: Прямые
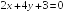 и
и
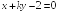 перпендикулярны при
перпендикулярны при
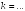
+: -1/2
I:
S: Прямые
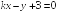 и
и
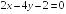 перпендикулярны при
перпендикулярны при

+: -2
V2: Кривые второго порядка.
I:
S: Расстояние между фокусами
эллипса
![]() равно
…
равно
…
+: 6
I:
S: Расстояние
между фокусами эллипса
 равно
…
равно
…
+: 16
I:
S: Расстояние между фокусами
гиперболы
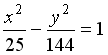 равно
…
равно
…
+: 26
I:
S: Расстояние между фокусами
гиперболы
 равно
…
равно
…
+: 40
I:
S: Расстояние между фокусами
гиперболы
 равно
…
равно
…
+: 50
I:
S: Вещественная полуось
гиперболы, заданной уравнением
![]() ,
равна…
,
равна…
+: 3
I:
S: Мнимая полуось гиперболы,
заданной уравнением
![]() ,
равна…
,
равна…
+: 2
I:
S: Мнимая полуось
гиперболы, заданной уравнением
![]() ,
равна…
,
равна…
+: 4
I:
S: Мнимая полуось
гиперболы, заданной уравнением
![]() ,
равна…
,
равна…
+:5
I:
S: Большая
полуось эллипса, заданного уравнением
![]() ,
равна…
,
равна…
+: 5
I:
S: Если прямая – уравнение асимптоты гиперболы
– уравнение асимптоты гиперболы
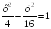 ,
то значение
,
то значение
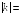 …
…
+: 2
I:
S: Если прямая – уравнение асимптоты гиперболы
– уравнение асимптоты гиперболы
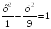 ,
то значение
,
то значение
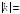 …
…
+: 3
I:
S: Если прямая – уравнение асимптоты гиперболы
– уравнение асимптоты гиперболы
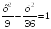 ,
то значение
,
то значение
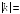 …
…
+: 2
I:
S: Уравнение
![]() определяет
окружность с центром в точке …
определяет
окружность с центром в точке …
+:
![]()
-:
![]()
-:
![]()
-:
![]()
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:
![]()
L2:
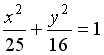
L3:

R1: Парабола
R2: Эллипс
R3: Гипербола
R4: окружность
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:
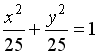
L2:
![]()
L3:
![]()
R1: окружность
R2: эллипс
R3: парабола
R4: гипербола
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:
![]()
L2:
![]()
L3:

R1: парабола
R2: эллипс
R3: окружность
R4: гипербола
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:
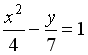
L2:
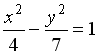
L3:

R1: парабола
R2: гипербола
R3: эллипс
R4: окружность
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:

L2:
![]()
L3:
![]()
R1: окружность
R2: эллипс
R3: парабола
R4: гипербола
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:
![]()
L2:
![]()
L3:

R1: парабола
R2: окружность
R3: гипербола
R4: эллипс
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:
![]()
L2:
![]()
L3:

R1: парабола
R2: гипербола
R3: эллипс
R4: окружность
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:
![]()
L2:
![]()
L3:
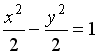
R1: эллипс
R2: парабола
R3: гипербола
R4: окружность
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:
![]()
L2:
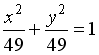
L3:

R1: парабола
R2: окружность
R3: гипербола
R4: эллипс
I:
S: Укажите соответствие между уравнениями и видами кривых второго порядка.
L1:
![]()
L2:
![]()
L3:
![]()
R1: окружность
R2: парабола
R3: эллипс
R4: гипербола
V2: Аналитическая геометрия в пространстве
I:
S: Нормальный вектор плоскости
![]() имеет
координаты…
имеет
координаты…
-: (7; 0; – 1)
+: (7; – 1; – 1)
-: (– 7; 1; 1)
-: (7; 0; 0)
I:
S: Вектор
![]() перпендикулярен
плоскости
перпендикулярен
плоскости
![]() .
Тогда значение p равно …
.
Тогда значение p равно …
-: 10
-: – 6
+: – 4
-: 6
I:
S: Плоскости
![]() и
и
![]() параллельны
при значениях
параллельны
при значениях
![]() и
и
![]() ,
равных …
,
равных …
-:
![]() ;
;
![]()
-:
![]() ;
;
![]()
+:
![]() ;
;
![]()
-:
![]() ;
;
![]()
I:
S: Координата
![]() точки
точки
![]() ,
принадлежащей плоскости
,
принадлежащей плоскости
![]() ,
равна…
,
равна…
-: 5
+: 3
-: 4
-: 2
I:
S: Координата
![]() точки
точки
![]() ,
принадлежащей плоскости
,
принадлежащей плоскости
![]() ,
равна…
,
равна…
-: 7
-: 10
-: 13
+: 11
I:
S: Координата
![]() точки
точки
![]() ,
принадлежащей плоскости
,
принадлежащей плоскости
![]() ,
равна…
,
равна…
-: 5
-: 3
-: 6
+: 4
I:
S: Координата
![]() точки
точки
![]() ,
принадлежащей плоскости
,
принадлежащей плоскости
![]() ,
равна…
,
равна…
+: 2
-: 3
-: 4
-: 1
I:
S: Координата
![]() точки
точки
![]() ,
принадлежащей плоскости
,
принадлежащей плоскости
![]() ,
равна…
,
равна…
-: 4
-: 1
-: 2
+: 3
I:
S: Уравнение прямой, проходящей
через точку
![]() перпендикулярно
плоскости
перпендикулярно
плоскости
![]() ,
имеет вид…
,
имеет вид…
-:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S: Уравнение прямой, проходящей
через точку
![]() перпендикулярно
плоскости
перпендикулярно
плоскости
![]() ,
имеет вид…
,
имеет вид…
+:
![]()
-:
![]()
-:
![]()
-:
![]()
I:
S: Уравнение
прямой, проходящей через точку
![]() перпендикулярно
плоскости
перпендикулярно
плоскости
![]() ,
имеет вид…
,
имеет вид…
-:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S: Уравнение
прямой, проходящей через точку
![]() перпендикулярно
плоскости
перпендикулярно
плоскости
![]() ,
имеет вид…
,
имеет вид…
-:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S: Точкой пересечения плоскости
![]() с
осью
с
осью
![]() является
…
является
…
-:
![]()
-:
![]()
-:
![]()
+:
![]()
V1: Комплексные числа
V2: Комплексные числа и их представление.
I:
S: Модуль комплексного числа
![]() равен …
равен …
-: 2
-: 14
+: 10
-:
![]()
I:
S: Установите соответствие между комплексным числом и его модулем
L1:
![]()
L2:
![]()
L3:
![]()
L4:
![]()
R1: 5
R2: 2
R3: 3
R4: 13
R5: 7
I:
S: Аргумент комплексного
числа
![]() равен …
равен …
-:
![]()
+:
![]()
-: 2
-:
![]()
I:
S: Установите соответствие между комплексным числом и его аргументом
L1:
![]()
L2:
![]()
L3:
![]()
R1:
![]()
R2:
![]()
R3:
![]()
R4:
![]()
I:
S: Установите соответствие между комплексным числом и его аргументом
L1:
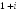
L2:

L3:

R1:
![]()
R2:
![]()
R3:
![]()
R4:
![]()
I:
S: Установите соответствие между комплексным числом и его аргументом
L1:
![]()
L2:
![]()
L3:
![]()
R1:
![]()
R3:
![]()
R2:
![]()
R4:
![]()
I:
S: Установите соответствие между комплексным числом и его аргументом
L1:
![]()
L2:
![]()
L3:
![]()
R1:
![]()
R2:
![]()
R3:
![]()
R4:
![]()
I:
S: Комплексное число
![]() в
тригонометрической форме имеет вид …
в
тригонометрической форме имеет вид …
-:

-:
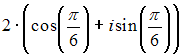
+:
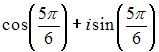
-:
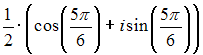
I:
S: Задано комплексное число
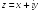 .
Установите соответствие:
.
Установите соответствие:
L1:
L2: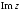
L3:
R1: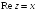
R2:
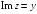
R3:
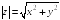
R4:

R5:
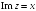
I:
S: Тригонометрическая форма записи комплексного числа имеет вид:
+:

-:

-:
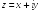
-:

I:
S: Показательная форма записи комплексного числа имеет вид:
-:

-:

-:

+:

I:
S: Алгебраическая форма записи комплексного числа имеет вид:
-:
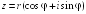
-:
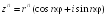
+:

-:
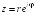
I:
S: Установите соответствие между формой записи комплексного числа и ее названием:
L1:

L2:

L3:
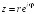
R1: тригонометрическая
R2: алгебраическая
R3: показательная
R4: степенная
V2: Операции над комплексными числами.
I:
S: Если
![]() –
решение линейного уравнения
–
решение линейного уравнения ![]() ,
то
,
то
![]() равно …
равно …
-:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S: Если
![]() и
и
![]() ,
то выражение
,
то выражение
![]() равно …
равно …
+:
![]()
-:
![]()
-:
![]()
-:
![]()
I:
S: Значение выражения
![]() равно …
равно …
-:
![]()
+:
![]()
-:
![]()
-:
![]()
I:
S: Значение функции
![]() в
точке
в
точке
![]() равно…
равно…
-:
![]()
+:
![]()
-:
![]()
-:
![]()
I:
S: Значение функции
![]() в
точке
в
точке![]() равно…
равно…
-:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S: Значение функции
![]() в
точке
в
точке
![]() равно…
равно…
+: – 9 – 15i
-: 15 – 15i
-: – 9 – 9i
-: 15 – 9i
I:
S: Значение функции
![]() в
точке
в
точке![]() равно…
равно…
-: – 9 – 15i
-: 15 – 15i
+: – 9 + 9i
-: 15 – 9i
I:
S: Значение функции
![]() в
точке
в
точке
![]() равно…
равно…
-: 40 + 13i
+: – 32 + 25i
-: – 32 + 13i
-: 40 + 25i
I:
S: Значение функции
![]() в
точке
в
точке![]() равно…
равно…
-: 40 + 13i
-: – 32 + 25i
+: – 32 – 23i
-: 40 + 25i
I:
S: Значение функции
![]() в
точке
в
точке
![]() равно…
равно…
-: 4 – 8i
-: – 6i
+: – 8i
-: 4 – 6i
I:
S: Значение функции
![]() в
точке
в
точке![]() равно…
равно…
-: 8i
-: – 8i
+: 0
-: 4 – 6i
I:
S: Если![]() ,
то
,
то![]() равно …
равно …
+: 16
-: 2i
-: 16i
-: 2
I:
S: Если
![]() ,
то сумма всех значений квадратного
корня из
,
то сумма всех значений квадратного
корня из![]() равна …
равна …
