
Математика_2013_080200_оч_полн_1_сем_зач
.docxАВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЦЕНТРОСОЮЗА РОССИЙСКОЙ ФЕДЕРАЦИИ
«РОССИЙСКИЙ УНИВЕРСИТЕТ КООПЕРАЦИИ»
КАЗАНСКИЙ КООПЕРАТИВНЫЙ ИНСТИТУТ (ФИЛИАЛ)

Математика
ТЕСТОВЫЕ ЗАДАНИЯ
Тестовые задания обсуждены на заседании кафедры инженерно- технических дисциплин и сервиса «24» сентября 2012 г. протокол № 2
Заведующий
кафедрой  /А.М.
Мухаметшин/
/А.М.
Мухаметшин/
СОГЛАСОВАНО
Начальник
отдела менеджмента качества
 /Д.Н.
Алюшева/
/Д.Н.
Алюшева/
ПАСПОРТ
|
№ |
Наименование пункта |
Значение |
|
|
Кафедра |
Инженерно-технические дисциплины и сервис |
|
|
Автор – разработчик |
Поташев А.В., д.ф.-м.н., профессор Поташева Е.В., к.т.н., доцент |
|
|
Наименование дисциплины |
Математика |
|
|
Общая трудоемкость по учебному плану |
108 (1 семестр) |
|
|
Вид контроля (нужное подчеркнуть) |
Предварительный (входной), текущий, промежуточный (зачет) |
|
|
Для специальности(ей)/ направления(й) подготовки |
080200.62 «Менеджмент» нормативный срок очная форма обучения |
|
|
Количество тестовых заданий всего по дисциплине, из них |
505 |
|
|
Количество заданий при тестировании студента |
25 |
|
|
Из них правильных ответов (в %): |
|
|
|
для оценки «отлично» |
86 % и больше |
|
|
для оценки «хорошо» |
71 % - 85% |
|
|
для оценки «удовлетворительно» |
56% - 70% |
|
|
или для получения оценки «зачет» не менее |
55% |
|
|
Время тестирования (в минутах) |
45 |
F1: Математиказачет1 семестр 2012/2013
F2: Поташев А.В., Поташева Е.В.
F3: Тестовые задания по направлению подготовки 080200.62 «Менеджмент»очнаянормативный срок505 задания, 25 вопросов
F4: Дидактическая единица; Раздел; Тема
V1: Линейная алгебра
V2: Определители
I:
S: Формула вычисления
определителя третьего порядка
 содержит следующие произведения: …
содержит следующие произведения: …
+:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S: Формула вычисления
определителя третьего порядка
 содержит следующие произведения: …
содержит следующие произведения: …
+:
![]()
-:
![]()
+:
![]()
-:![]()
I:
S: Формула
вычисления определителя третьего
порядка
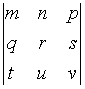 содержит
следующие произведения: …
содержит
следующие произведения: …
+:
![]()
+:
![]()
-:
![]()
-:
![]()
I:
S: Формула
вычисления определителя третьего
порядка
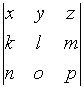 содержит
следующие произведения: …
содержит
следующие произведения: …
+:
![]()
+:
![]()
-:
![]()
-:
![]()
I:
S: Формула вычисления
определителя третьего порядка
 содержит
следующие произведения: …
содержит
следующие произведения: …
+:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S: Формула вычисления
определителя третьего порядка
 содержит
следующие произведения: …
содержит
следующие произведения: …
-:
![]()
-:
![]()
+:
![]()
+:
![]()
I:
S: Формула вычисления
определителя третьего порядка
 содержит
следующие произведения: …
содержит
следующие произведения: …
-:
![]()
+:
![]()
+:
![]()
-:
![]()
I:
S: Формула вычисления
определителя третьего порядка
 содержит
следующие произведения: …
содержит
следующие произведения: …
+:
![]()
+:
![]()
-:
![]()
-:
![]()
I:
S: Определитель
 равен…
равен…
-:
![]()
-:
![]()
-:
![]()
+:
![]()
I:
S: Разложение
определителя
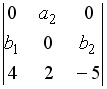 по
элементам первой строки имеет вид…
по
элементам первой строки имеет вид…
+:
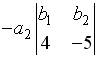
-:

-:

-:

I:
S: Определитель
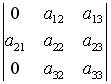 равен…
равен…
+:
![]()
-:
![]()
-:
![]()
-:
![]()
I:
S: Разложение
определителя
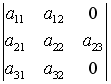 по
элементам третьего столбца имеет вид
…
по
элементам третьего столбца имеет вид
…
-:
![]()
+:
![]()
-:
![]()
-:
![]()
I:
S: Определитель
 равен
0, если
равен
0, если
![]() равно
…
равно
…
-: 2
-: – 4
-: 0
+: 1
I:
S: Определитель
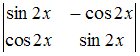 равен …
равен …
-: 0
-:
![]()
+: 1
-:
![]()
I:
S: Определитель
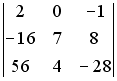 равен
…
равен
…
+: 0
I:
S: Определитель
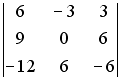 равен
…
равен
…
+: 0
I:
S: Определитель
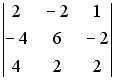 равен
…
равен
…
+: 0
I:
S: Определитель
 равен
…
равен
…
+: 35
I:
S: Определитель
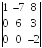 равен
…
равен
…
+: -12
I:
S: Определитель
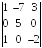 равен
…
равен
…
+: -25
I:
S: Определитель
 равен
…
равен
…
+: 2
I:
S: Определитель
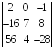 равен
…
равен
…
+: 0
I:
S: Определитель
 равен
…
равен
…
+: 0
I:
S: Определитель
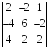 равен
…
равен
…
+: 0
V2: Линейные операции над матрицами
I:
S: Даны матрицы
 ,
,
 ,
,
 .
Тогда матрица
.
Тогда матрица
![]() равна
…
равна
…
-:
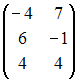
-:
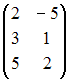
-:
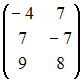
+:
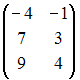
I:
S: Дана матрица
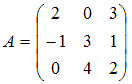 .
Если E – единичная матрица того же
размера, что и матрица A, то матрица
.
Если E – единичная матрица того же
размера, что и матрица A, то матрица
![]() равна …
равна …
+:

-:
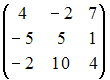
-:

-:
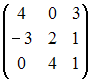
I:
S: Если
 ,
то матрица
,
то матрица
![]() имеет
вид...
имеет
вид...
-:

+:
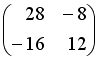
-:

-:
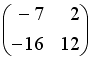
I:
S: Даны матрицы
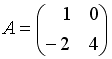 и
и
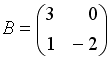 .
Тогда
.
Тогда
![]() равно
…
равно
…
-:
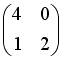
-:

-:
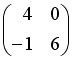
+:

I:
S: Даны матрицы
 ,
,
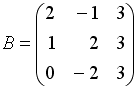 .
Тогда матрица
.
Тогда матрица
![]() равна…
равна…
-:
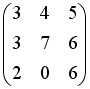
-:
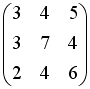
+:

-:

I:
S: Даны матрицы
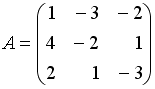 ,
,
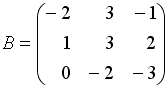 .
Тогда матрица
.
Тогда матрица
![]() равна
…
равна
…
-:
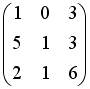
-:
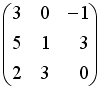
-:

+:
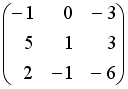
I:
S: Даны матрицы
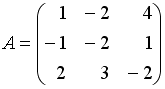 ,
,
 .
Тогда матрица
.
Тогда матрица
![]() равна
…
равна
…
-:

-:

+:

-:

I:
S: Если
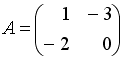 и
и
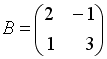 ,
то матрица
,
то матрица
![]() имеет
вид…
имеет
вид…
-:
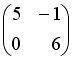
+:
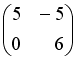
-:
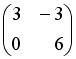
-:

I:
S: Если
 и
и
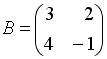 ,
то матрица
,
то матрица
![]() имеет
вид…
имеет
вид…
-:

-:
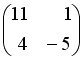
-:
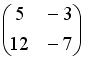
+:
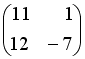
V2: Произведение матриц
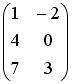
I:
S: Для матрицА и В найдено
произведение
![]() ,
причем
,
причем
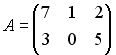 .
Тогда матрицей В может быть матрица
…
.
Тогда матрицей В может быть матрица
…
-:
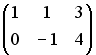
-:
![]()
+:
-:
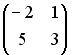
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
+:
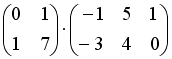
-:

+: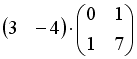
+: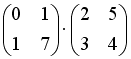
-:
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
-:
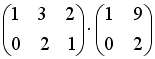
+:
-:
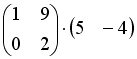
+:
+:
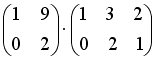
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
+:
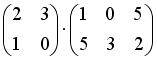
-:

+:
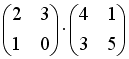
-:

+:
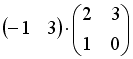
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
+:
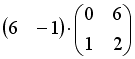
+:
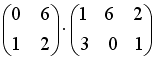
-:
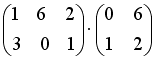
-:

+:
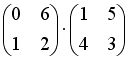
I:
S: Операция произведения матриц правильно определена для матричного произведения вида …
+:

+:
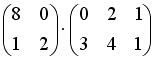
-:
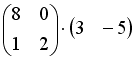
+:

-:

I:
S: Заданы матрицы
 ,
,
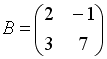 .
Тогда элемент
.
Тогда элемент
![]() матрицы
матрицы
![]() равен
…
равен
…
+: 3
-: −11
-: −7
-: 5
I:
S: Дана матрица
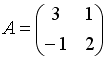 .
Тогда элемент
.
Тогда элемент
![]() матрицы
матрицы
![]() равен
…
равен
…
+: 5
-: – 5
-: – 1
-: 1
I:
S: Элемент
 в произведении матриц
в произведении матриц
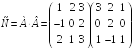 равен …
равен …
+: 3
I:
S: Элемент
 в произведении матриц
в произведении матриц
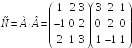 равен …
равен …
+: 6
I:
S: Элемент
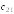 в произведении матриц
в произведении матриц
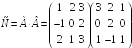 равен …
равен …
+: -1
I:
S: Элемент
 в произведении матриц
в произведении матриц
 равен …
равен …
+: 3
I:
S: Заданы матрицы
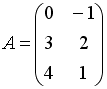 ,
,
 .
Тогда элемент
.
Тогда элемент
![]() матрицы
матрицы
![]() равен
…
равен
…
+: 3
-: − 11
-: − 7
-: 5
I:
S: Дана матрица 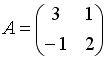 .
Тогда элемент
.
Тогда элемент
![]() матрицы
матрицы
![]() равен
…
равен
…
+: 5
-: – 5
-: – 1
-: 1
I:
S:Если
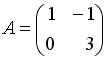 ,
,
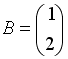 ,
тогда матрица
,
тогда матрица
![]() имеет
вид …
имеет
вид …
-:
![]()
+:
![]()
-:
![]()
-:
![]()
I:
S:Если
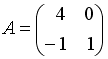 ,
,
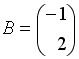 ,
тогда матрица
,
тогда матрица
![]() имеет
вид …
имеет
вид …
+:
![]()
-:
![]()
-:
![]()
-:
![]()
I:
S:Если
 ,
,
 ,
тогда матрица
,
тогда матрица
![]() имеет
вид …
имеет
вид …
-:

-:
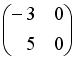
-:
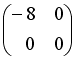
+:

I:
S:Если
 ,
,
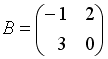 ,
тогда матрица
,
тогда матрица
![]() имеет
вид …
имеет
вид …
+:
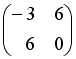
-:
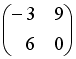
-:
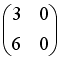
-:

I:
S: Дана матрица
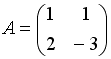 .
Тогда матрица
.
Тогда матрица
![]() имеет
вид …
имеет
вид …
-:
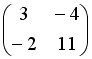
-:

-:
![]()
+:
I:
S: Дана матрица
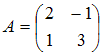 .
Тогда матрица
.
Тогда матрица
![]() имеет
вид …
имеет
вид …
-:
-:

+:
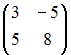
-:

I:
S: Дана матрица
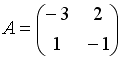 .
Тогда матрица
.
Тогда матрица
![]() имеет
вид …
имеет
вид …
