математике экзамен Сервис СПО_
.doc
Тогда математическое ожидание случайной
величины
равно…
+: 14,5
-: 20
-: 15,5
-: 7,9
I:{{368}} ТЗ-368 (ДЕ-10-24-0); t=0; k=; ek=0; m=0; c=0;
S: Дискретная случайная величина Х задана законом распределения вероятностей
.
Тогда значение интегральной функции
распределения вероятностей
равно
…
+: 0,2
-: 0,8
-: 0,6
-: 0,9
I:{{369}} ТЗ-369 (ДЕ-10-24-0); t=0; k=; ek=0; m=0; c=0;
S: Дискретная случайная
величина Х задана законом распределения
вероятностей
.
Тогда значение интегральной функции
распределения вероятностей
равно
…
-: 0,4
+: 0,6
-: 0,3
-: 0,9
V2: {{25}} 10.25. Непрерывная случайная величина
I:{{370}} ТЗ-370 (ДЕ-10-25-0); t=0; k=; ek=0; m=0; c=0;
S: График плотности
распределения вероятностей непрерывной
случайной величины Х, распределённой
равномерно в интервале
,
имеет вид:
Тогда значение a равно…
+:
-:
-: 1
-:
I:{{371}} ТЗ-371 (ДЕ-10-25-0); t=0; k=; ek=0; m=0; c=0;
S: Случайная величина
распределена
равномерно на отрезке
.
Распределение случайной величины
имеет...
-: другой (кроме равномерного и нормального) вид распределения
-: равномерное распределение на отрезке
+: равномерное распределение на отрезке
-: нормальное распределение на отрезке
I:{{372}} ТЗ-372 (ДЕ-10-25-0); t=0; k=; ek=0; m=0; c=0;
S: Случайная величина
распределена
равномерно на отрезке
.
Тогда случайная величина
имеет…
-: другой (не равномерный) вид распределения
-: равномерное распределение
на отрезке
-: равномерное распределение
на отрезке
+: равномерное распределение
на отрезке
I:{{373}} ТЗ-373 (ДЕ-10-25-0); t=0; k=; ek=0; m=0; c=0;
S: Случайная величина
распределена
равномерно на отрезке
..
Тогда случайная величина
имеет…
-: другой (кроме равномерного и нормального) вид распределения
+: равномерное распределение на отрезке
-: нормальное распределение на отрезке
-: равномерное распределение на отрезке
V2: {{26}} 10.26. Полная вероятность. Формула Байеса
I:{{374}} ТЗ-374 (ДЕ-10-26-0); t=0; k=; ek=0; m=0; c=0;
S: В первой урне 3 белых и 7 черных шаров. Во второй урне 6 белых и 4 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
-: 0,5
-: 0,9
+: 0,45
-: 0,15
I:{{375}} ТЗ-375 (ДЕ-10-26-0); t=0; k=; ek=0; m=0; c=0;
S: Имеются две одинаковые на вид урны. В первой урне находятся один белый и два черных шара. Во второй урне - два белых и два черных шара. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар белый равна …
-:
+:
-:
-:
I:{{376}} ТЗ-376 (ДЕ-10-26-0); t=0; k=; ek=0; m=0; c=0;
S: Имеются две одинаковые на вид урны. В первой урне находятся три красных и один черный шар. Во второй – два красных и один черный шар. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар красный равна …
-:
+:
-:
-:
I:{{377}} ТЗ-377 (ДЕ-10-26-0); t=0; k=; ek=0; m=0; c=0;
S: Имеются две одинаковые на вид урны. В первой урне находятся два белых и один черный шар. Во второй урне – семь белых и семь черных шаров. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар белый равна …
-:
-:
-:
+:
I:{{378}} ТЗ-378 (ДЕ-10-26-0); t=0; k=; ek=0; m=0; c=0;
S: В первом ящике 7 красных и 11 синих шаров, во втором – 5 красных и 9 синих. Из произвольного ящика достают один шар. Вероятность того, что он синий, равна…
-:
-:
+:
-:
I:{{379}} ТЗ-379 (ДЕ-10-26-0); t=0; k=; ek=0; m=0; c=0;
S: Событие А может наступить
лишь при условии появления одного из
двух несовместных событий
и
,
образующих полную группу событий.
Известны вероятность
и
условные вероятности
.
Тогда вероятность
равна
…
-:
-:
-:
+:
I:{{380}} ТЗ-380 (ДЕ-10-26-0); t=0; k=; ek=0; m=0; c=0;
S: Событие А может наступить
лишь при условии появления одного из
двух несовместных событий
и
,
образующих полную группу событий.
Известны вероятность
и
условные вероятности
.
Тогда вероятность
равна
…
-:
-:
+:
-:
I:{{381}} ТЗ-381 (ДЕ-10-26-0); t=0; k=; ek=0; m=0; c=0;
S: Событие А может наступить
лишь при условии появления одного из
двух несовместных событий
и
,
образующих полную группу событий.
Известны вероятность
и
условные вероятности
.
Тогда вероятность
равна
…
-:
-:
-:
+:
I:{{382}} ТЗ-382 (ДЕ-10-26-0); t=0; k=; ek=0; m=0; c=0;
S: В первой урне 1 черный и 9 белых шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
+: 0,65
-: 0,13
-: 0,7
-: 0,25
I:{{383}} ТЗ-383 (ДЕ-10-26-0); t=0; k=; ek=0; m=0; c=0;
S: В первой урне 5 белых и 5 черных шаров. Во второй урне 3 черных и 7 белых шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
-: 0,1
-: 0,65
+: 0,6
-: 0,12
V1: {{11}} 11. Численные методы
V2: {{27}} 11.27. Численные методы решения алгебраических уравнений
I:{{384}} ТЗ-384 (ДЕ-11-27-0); t=0; k=; ek=0; m=0; c=0;
S: Действительный корень
уравнения
принадлежит
интервалу…
-:
-:
+:
-:
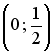
I:{{385}} ТЗ-385 (ДЕ-11-27-0); t=0; k=; ek=0; m=0; c=0;
S: Действительный корень
уравнения
принадлежит
интервалу…
-:
+:
-:
-:
I:{{386}} ТЗ-386 (ДЕ-11-27-0); t=0; k=; ek=0; m=0; c=0;
S: Действительный корень
уравнения
принадлежит
интервалу…
-:
+:
-:
-:
I:{{387}} ТЗ-387 (ДЕ-11-27-0); t=0; k=; ek=0; m=0; c=0;
S: Три итерации метода
половинного деления при решении уравнения
на
отрезке
требуют
последовательного вычисления значений
функции
в
точках...
-:
-:
+:
-:
I:{{388}} ТЗ-388 (ДЕ-11-27-0); t=0; k=; ek=0; m=0; c=0;
S: Три итерации метода
половинного деления при решении уравнения
на
отрезке
требуют
последовательного вычисления значений
функции
в
точках...
-:
-:
-:
+:
I:{{389}} ТЗ-389 (ДЕ-11-27-0); t=0; k=; ek=0; m=0; c=0;
S: Три итерации метода
половинного деления при решении уравнения
на
отрезке
требуют
последовательного вычисления значений
функции
в точках...
+:
-:
-:
-:
I:{{390}} ТЗ-390 (ДЕ-11-27-0); t=0; k=; ek=0; m=0; c=0;
S: Три итерации метода
половинного деления при решении уравнения
на
отрезке
требуют
последовательного вычисления значений
функции
в точках...
+:
-:
-:
-:
I:{{391}} ТЗ-391 (ДЕ-11-27-0); t=0; k=; ek=0; m=0; c=0;
S: Три итерации метода
половинного деления при решении уравнения
на
отрезке
требуют
последовательного вычисления значений
функции
в точках...
+:
-:
-:
-:
I:{{392}} ТЗ-392 (ДЕ-11-27-0); t=0; k=; ek=0; m=0; c=0;
S: Три итерации метода
половинного деления при решении уравнения
на
отрезке
требуют
последовательного вычисления значений
функции
в точках...
+:
-:
-:
-:
I:{{393}} ТЗ-393 (ДЕ-11-27-0); t=0; k=; ek=0; m=0; c=0;
S: Три итерации метода
половинного деления при решении уравнения
на
отрезке
требуют
последовательного вычисления значений
функции
в точках...
+:
-:
-:
-:
V2: {{28}} 11.28. Численные методы решения дифференциальных уравнений
I:{{394}} ТЗ-394 (ДЕ-11-28-0); t=0; k=; ek=0; m=0; c=0;
S: Дано дифференциальное
уравнение
при
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид …
+:
-:
-:
-:
I:{{395}} ТЗ-395 (ДЕ-11-28-0); t=0; k=; ek=0; m=0; c=0;
S: Дано дифференциальное
уравнение
при
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид …
-:
-:
-:
+:
I:{{396}} ТЗ-396 (ДЕ-11-28-0); t=0; k=; ek=0; m=0; c=0;
S: Дано дифференциальное
уравнение
при
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
-:
-:
+:
-:
I:{{397}} ТЗ-397 (ДЕ-11-28-0); t=0; k=; ek=0; m=0; c=0;
S: Дано дифференциальное
уравнение
при
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
-:
-:
-:
+:
I:{{398}} ТЗ-398 (ДЕ-11-28-0); t=0; k=; ek=0; m=0; c=0;
S: Дано дифференциальное
уравнение
при
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
-:
+:
-:
-:
I:{{399}} ТЗ-399 (ДЕ-11-28-0); t=0; k=; ek=0; m=0; c=0;
S: Дано дифференциальное
уравнение
при
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
-:
+:
-:
-:
I:{{400}} ТЗ-400 (ДЕ-11-28-0); t=0; k=; ek=0; m=0; c=0;
S: Дано дифференциальное
уравнение
при
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
+:
-:
-:
-:
I:{{401}} ТЗ-401 (ДЕ-11-28-0); t=0; k=; ek=0; m=0; c=0;
S: Дано дифференциальное
уравнение
при
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
-:
+:
-:
-:
I:{{402}} ТЗ-402 (ДЕ-11-28-0); t=0; k=; ek=0; m=0; c=0;
S: Дано дифференциальное
уравнение
при
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
+:
-:
-:
-:
I:{{403}} ТЗ-403 (ДЕ-11-28-0); t=0; k=; ek=0; m=0; c=0;
S: Дано дифференциальное
уравнение
при
.Тогда
первые три члена разложения его решения
в степенной ряд имеют вид ...
+:
-:
-:
-:
I:{{404}} ТЗ-404 (ДЕ-11-28-0); t=0; k=; ek=0; m=0; c=0;
S: Дано дифференциальное
уравнение
при
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
+:
-:
-:
-:
I:{{405}} ТЗ-405 (ДЕ-11-28-0); t=0; k=; ek=0; m=0; c=0;
S: Дано дифференциальное
уравнение
при
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
+:
-:
-:
-:
V2: {{29}} 11.29. Численное дифференцирование и интегрирование
I:{{406}} ТЗ-406 (ДЕ-11-29-0); t=0; k=; ek=0; m=0; c=0;
S: Формула прямоугольников
приближенного вычисления определенного
интеграла, соответствующая рисунку,
имеет вид …