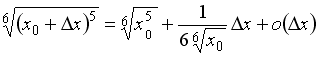- •V1: Дифференциальные уравнения
- •V2: Типы дифференциальных уравнений
- •V2: Дифференциальные уравнения первого порядка
- •V2: Дифференциальные уравнения высших порядков
- •V2: Линейные дифференциальные уравнения 2 порядка. Характеристическое уравнение
- •V2: Линейные дифференциальные уравнения 2 порядка. Частное решение
- •V1: Ряды
- •V2: Признаки сходимости числовых рядов
- •V2: Знакоположительные ряды
- •V2: Знакочередующиеся ряды
- •V2: Радиус сходимости степенного ряда
- •V2: Ряды Тейлора (Маклорена)
- •V1: Численные методы
- •V2: Численные методы решения алгебраических уравнений
- •V2: Численные методы решения дифференциальных уравнений
- •V2: Численное интегрирование
- •V2: Приближенное значение функции
-
V2: Численные методы решения дифференциальных уравнений
-
I:
-
S: Дано
дифференциальное уравнение
![]() при
при
![]() .
Тогда первые три члена разложения его
решения в степенной ряд имеют вид …
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид …
+:
![]()
-:
![]()
-:
![]()
-:
![]()
-
I:
S: Дано
дифференциальное уравнение
![]() при
при
![]() .
Тогда первые три члена разложения его
решения в степенной ряд имеют вид …
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид …
-:
![]()
-:
![]()
-:
![]()
+:
![]()
-
I:
S: Дано
дифференциальное уравнение
![]() при
при
![]() .
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
-:
![]()
-:
![]()
+:
![]()
-:
![]()
-
I:
S: Дано
дифференциальное уравнение
![]() при
при
![]() .
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
-:
![]()
-:
![]()
-:
![]()
+:
![]()
-
I:
S: Дано
дифференциальное уравнение
![]() при
при
![]() .
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
-:
![]()
+:
![]()
-:
![]()
-:
![]()
-
I:
S: Дано
дифференциальное уравнение
![]() при
при
![]() .
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
-:
![]()
+:
![]()
-:
![]()
-:
![]()
-
I:
S: Дано
дифференциальное уравнение![]() при
при
![]() .
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
+:
![]()
-:
![]()
-:
![]()
-:
![]()
-
I:
S: Дано
дифференциальное уравнение
![]() при
при
![]() .
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
-:
![]()
+:
![]()
-:
![]()
-:
![]()
-
I:
S: Дано
дифференциальное уравнение![]() при
при
![]() .
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
+:
![]()
-:
![]()
-:
![]()
-:
![]()
-
I:
S: Дано
дифференциальное уравнение![]() при
при
![]() .Тогда
первые три члена разложения его решения
в степенной ряд имеют вид ...
.Тогда
первые три члена разложения его решения
в степенной ряд имеют вид ...
+:
![]()
-:
![]()
-:
![]()
-:
![]()
-
I:
S: Дано
дифференциальное уравнение![]() при
при
![]() .
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
+:
![]()
-:
![]()
-:
![]()
-:
![]()
-
I:
S: Дано
дифференциальное уравнение![]() при
при
![]() .
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
.
Тогда первые три члена разложения его
решения в степенной ряд имеют вид ...
+:
![]()
-:
![]()
-:
![]()
-:
![]()
-
V2: Численное интегрирование
-
I:
-
S: Формула
прямоугольников приближенного вычисления
определенного интеграла, соответствующая
рисунку, имеет вид …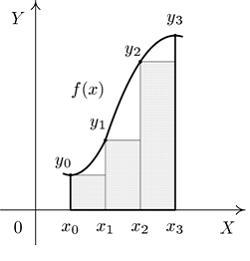
-:
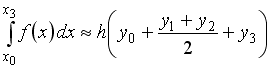
+:
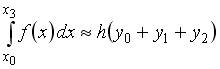
-:
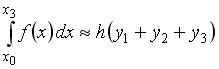
-:
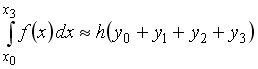
-
I:
S: Формула
прямоугольников приближенного вычисления
определенного интеграла, соответствующая
рисунку, имеет вид …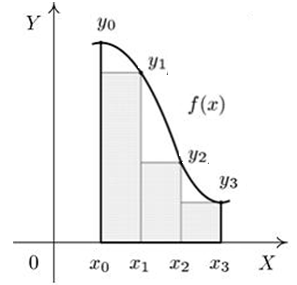
-:
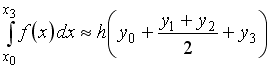
-:
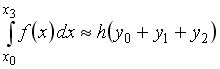
+:
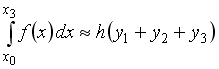
-:
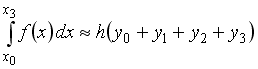
-
I:
S: Формула левых прямоугольников для приближенного вычисления определенного интеграла от функции f(x), заданной на отрезке [0,2], имеет вид:
+:
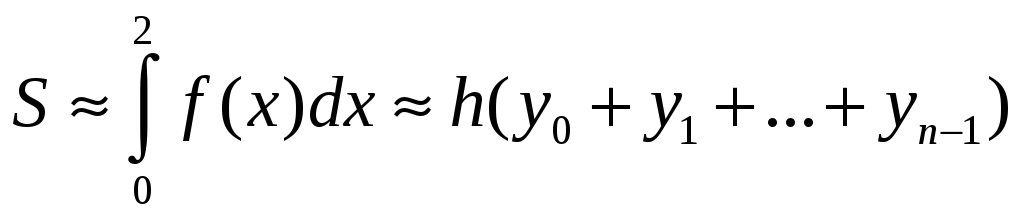
-:
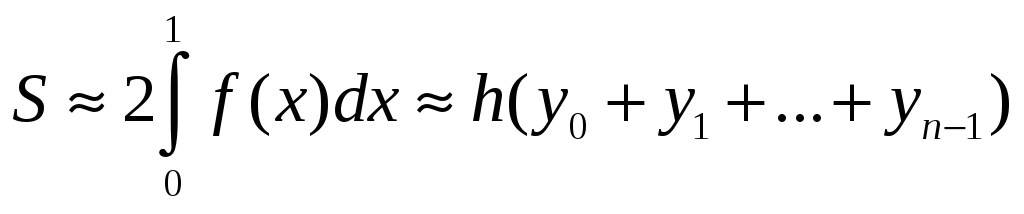
-:
![]()
-:
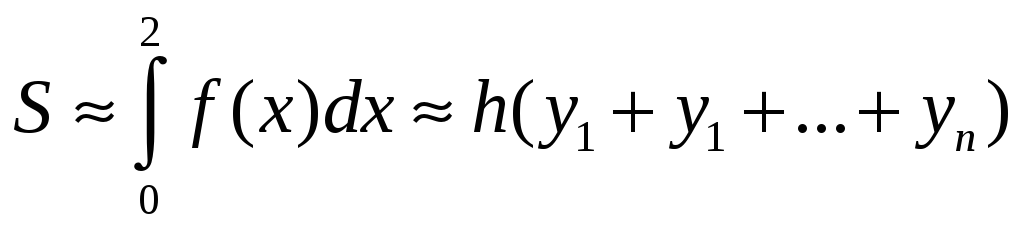
-
I:
S: Формула правых прямоугольников для приближенного вычисления определенного интеграла от функции f(x), заданной на отрезке [2,4], имеет вид:
-:
![]()
-:
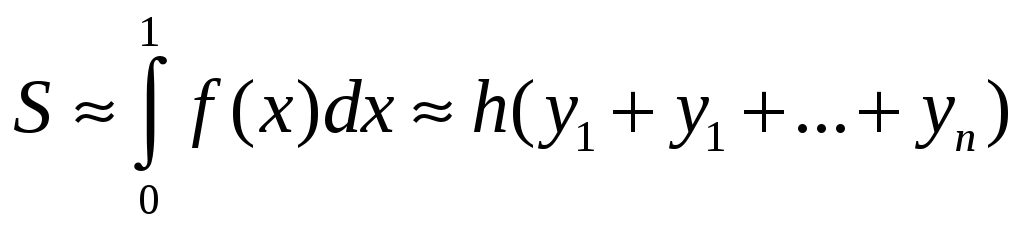
-:
![]()
+:
![]()
-
I:
S: Формула трапеции для приближенного вычисления определенного интеграла от функции f(x), заданной на отрезке [0,2], имеет вид:
+:
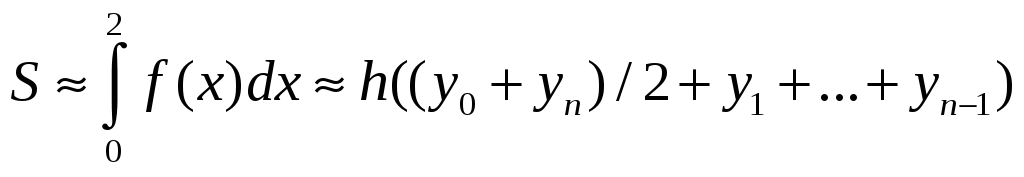
-:

-:
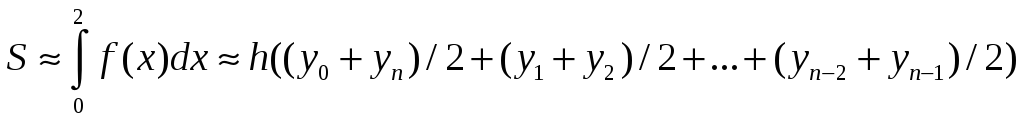
-:
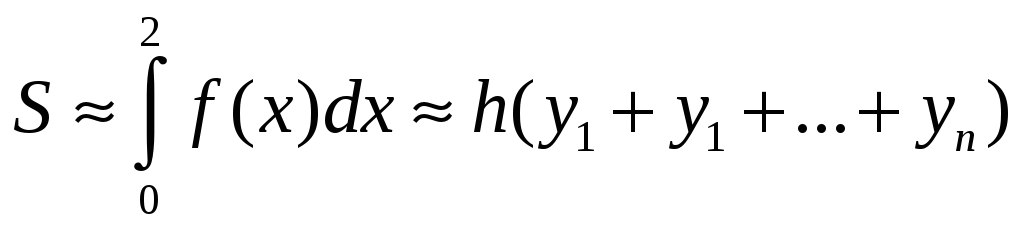
-
V2: Приближенное значение функции
-
I:
-
S: Значение
функции
![]() в
точке
в
точке
![]() можно
вычислить по формуле …
можно
вычислить по формуле …
-:
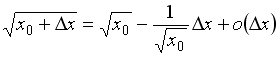
-:
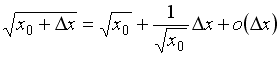
-:
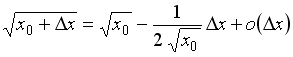
+:
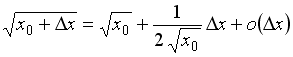
-
I:
S: Значение
функции
![]() в
точке
в
точке
![]() можно
вычислить по формуле …
можно
вычислить по формуле …
-:
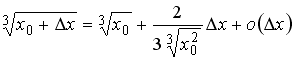
-:
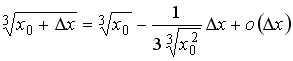
-:
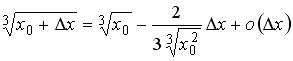
+:
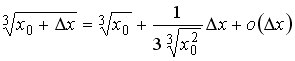
-
I:
S: Значение
функции
![]() в
точке
в
точке
![]() можно
вычислить по формуле …
можно
вычислить по формуле …
-:
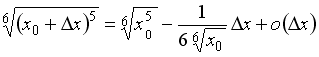
-:
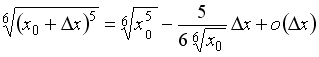
+:

-: