
- •V1: Дифференциальные уравнения
- •V2: Типы дифференциальных уравнений
- •V2: Дифференциальные уравнения первого порядка
- •V2: Дифференциальные уравнения высших порядков
- •V2: Линейные дифференциальные уравнения 2 порядка. Характеристическое уравнение
- •V2: Линейные дифференциальные уравнения 2 порядка. Частное решение
- •V1: Ряды
- •V2: Признаки сходимости числовых рядов
- •V2: Знакоположительные ряды
- •V2: Знакочередующиеся ряды
- •V2: Радиус сходимости степенного ряда
- •V2: Ряды Тейлора (Маклорена)
- •V1: Численные методы
- •V2: Численные методы решения алгебраических уравнений
- •V2: Численные методы решения дифференциальных уравнений
- •V2: Численное интегрирование
- •V2: Приближенное значение функции
Тема. 1. V1: Дифференциальные уравнения 1
I. V2: Типы дифференциальных уравнений 1
II. V2: Дифференциальные уравнения первого порядка 3
III. V2: Дифференциальные уравнения высших порядков 5
IV. V2: Линейные дифференциальные уравнения 2 порядка. Характеристическое уравнение 6
V. V2: Линейные дифференциальные уравнения 2 порядка. Частное решение 8
Тема. 2. V1: Ряды 10
I. V2: Признаки сходимости числовых рядов 10
II. V2: Знакоположительные ряды 11
III. V2: Знакочередующиеся ряды 14
IV. V2: Радиус сходимости степенного ряда 15
V. V2: Ряды Тейлора (Маклорена) 17
Тема. 3. V1: Численные методы 19
I. V2: Численные методы решения алгебраических уравнений 19
II. V2: Численные методы решения дифференциальных уравнений 21
III. V2: Численное интегрирование 23
IV. V2: Приближенное значение функции 24
F1:Математика 2 семестр экзамен очное полный
F2: Поташев А.В., Поташева Е.В.
F3:
F4: Дидактическая единица; Тема
-
V1: Дифференциальные уравнения
-
V2: Типы дифференциальных уравнений
-
I:
-
-
S: Среди перечисленных дифференциальных уравнений уравнениями первого порядка являются:
+:
![]()
-:
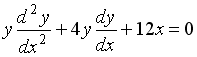
+:
![]()
-:
![]()
-
I:
S: Среди перечисленных дифференциальных уравнений уравнениями второго порядка являются:
-:

+:

-:
![]()
+:
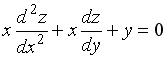
-
I:
S: Среди перечисленных дифференциальных уравнений уравнениями второго порядка являются:
+:

+:
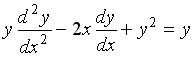
-:
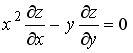
-:
![]()
-
I:
S: Среди перечисленных дифференциальных уравнений уравнениями второго порядка являются:
-:
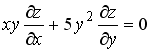
-:
![]()
+:

+:

-
I:
S: Из данных дифференциальных уравнений уравнениями Бернулли являются…
+:
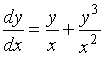
-:
![]()
-:
![]()
+:
![]()
-
I:
S: Укажите дифференциальное уравнение первого порядка.
+:

+:
![]()
-:
![]()
-:
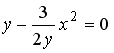
-
I:
S: Укажите дифференциальное уравнение первого порядка.
-:
![]()
+:
![]()
+:
![]()
-:
![]()
-
I:
S: Укажите дифференциальное уравнение первого порядка.
-:
![]()
-:
![]()
+:
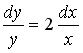
+:
![]()
-
I:
S: Дифференциальными уравнениями первого порядка являются …
-:
![]()
+:
![]()
-:
![]()
+:
![]()
-
I:
S: Дифференциальными уравнениями первого порядка являются …
+:
![]()
+:
![]()
-:
![]()
-:
![]()
-
V2: Дифференциальные уравнения первого порядка
-
I:
-
S: Общий интеграл
дифференциального уравнения
![]() имеет
вид…
имеет
вид…
+:
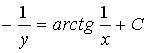
-:
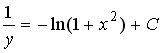
-:

-:
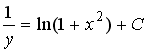
-
I:
S: Общее решение
дифференциального уравнения
![]() имеет вид
имеет вид
-:
![]()
-:
![]()
+:
![]()
-:

-
I:
S: Общее решение
дифференциального уравнения
![]() имеет
вид
имеет
вид
+:
![]()
-:
![]()
-:
![]()
-:
![]()
-
I:
S: Если
дифференциальное уравнение имеет вид
![]() ,
,
![]() ,
,
то в общем
решении
![]() произвольная
постоянная С равна …
произвольная
постоянная С равна …
+: 15
-
I:
S: Если
дифференциальное уравнение имеет вид
![]() ,
,![]()
то в общем
решении
![]() произвольная постоянная С равна
…
произвольная постоянная С равна
…
+: 4
-
I:
S: Если
дифференциальное уравнение имеет вид
![]() ,
,
![]()
то в общем
решении
![]() при произвольная постоянная С равна
…
при произвольная постоянная С равна
…
+: -3
-
I:
S: Если
дифференциальное уравнение имеет вид
![]() ,
,
![]()
то в общем
решении
![]() произвольная постоянная С равна
…
произвольная постоянная С равна
…
+: -7
-
I:
S: Если
дифференциальное уравнение имеет вид
![]() ,
,
![]()
то в общем
решении
![]() произвольная постоянная С равна …
произвольная постоянная С равна …
+: 3
-
I:
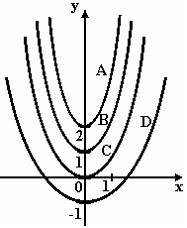
S: Дано
дифференциальное уравнение
![]() при
у(1)=1. Тогда интегральная кривая, которая
определяет решение этого уравнения,
имеет вид…
при
у(1)=1. Тогда интегральная кривая, которая
определяет решение этого уравнения,
имеет вид…
-: В
+: С
-: D
-: A
-
I:
S: Дано
дифференциальное уравнение
![]() при у(0)= -1. Тогда интегральная кривая,
которая определяет решение этого
уравнения, имеет вид…
при у(0)= -1. Тогда интегральная кривая,
которая определяет решение этого
уравнения, имеет вид…
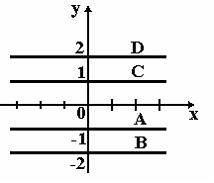
-: B
-: C
+: A
-: D
-
V2: Дифференциальные уравнения высших порядков
-
I:
-
S: Общее решение
дифференциального уравнения
![]() имеет вид
имеет вид
-:
![]()
-:
![]()
-:
![]()
+:
![]()
-
I:
S: Общее решение
дифференциального уравнения
![]() имеет
вид
имеет
вид
-:
![]()
+:
![]()
-:
![]()
-:
![]()
-
I:
S: Общее решение
дифференциального уравнения
![]() имеет
вид
имеет
вид
+:
![]()
-:
![]()
-:
![]()
-:
![]()
-
I:
S: Общее решение
дифференциального уравнения
![]() имеет
вид
имеет
вид
-:
![]()
-:
![]()
-:
![]()
+:
![]()
-
I:
S: Общее решение
дифференциального уравнения
![]() имеет
вид
имеет
вид
-:
![]()
-:
![]()
-:
![]()
+:
![]()
