Вариант 5

1. Найти область определения функции .

2. Построить линии уровня функции.

3. Вычислить частные производные первых и вторых порядков функции двух переменных .

4. Вычислить полный дифференциал функции в точке.

5. Исследовать на экстремум функцию .

6. Найти наибольшее и наименьшее значения функции в прямоугольнике, ограниченном прямымих = 1 ,х = 3,у = -1,у = 1. .

7. Найти градиент функции в точке.

8. Найти производную функции в направлении векторав точке.

9. Провести касательную плоскость к поверхности в точке.

10. Экспериментально получены пять значений искомой функции у=f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию у=f(x) в виде у=ах+b.

х	1	2	3	4	5
у	5,1	6,1	4,6	2,6	3,1

11. Вычислить двойной интеграл , гдеD– область, ограниченная линиями.

12. Требуется изготовить из жести ведро без крышки данного объема V, цилиндрической формы. Каковы должны быть высота цилиндра и радиус основания, чтобы на изготовление ведра ушло наименьшее количество материала?

Вариант 6

1. Найти область определения функции .

2. Построить линии уровня функции .

3. Вычислить частные производные первых и вторых порядков функции двух переменных .

4. Вычислить полный дифференциал функции в точке.

5. Исследовать на экстремум функцию .

6. Найти наибольшее и наименьшее значения функции в прямоугольнике, ограниченном прямымих = -1 ,х = 1,у = -1,у = 1 .

7. Найти градиент функции в точке.

8. Найти производную функции в направлении векторав точке.

9. Написать уравнение нормали к поверхности в точке.

10. Экспериментально получены пять значений искомой функции у=f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию у=f(x) в виде у=ах+b.

х	1	2	3	4	5
у	3,9	4,9	3,4	1,4	1,9

11. Вычислить двойной интеграл , гдеD– область, ограниченная линиями.

12. При каких линейных размерах закрытая цилиндрическая банка данной вместимости Vбудет иметь наименьшую полную поверхность?

Вариант 7

1. Найти область определения функции .

2. Построить линии уровня функции .

3. Вычислить частные производные первых и вторых порядков функции двух переменных .

4. Вычислить полный дифференциал функции в точке.

5. Исследовать на экстремум функцию .

6. Найти наибольшее и наименьшее значения функции 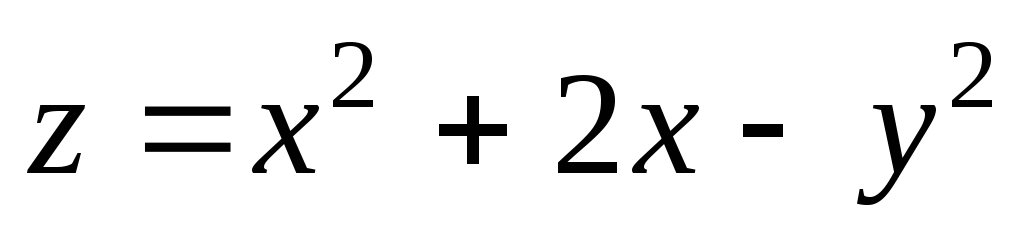в прямоугольнике, ограниченном прямымих = -3 ,х = 0,у = -1,у = 1.

7. Найти градиент функции в точке.

8. Найти производную функции в направлении векторав точке.

9. Написать уравнение касательной плоскости к поверхности в точке.

10. Экспериментально получены пять значений искомой функции у=f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию у=f(x) в виде у=ах+b.

х	1	2	3	4	5
у	5,2	6,2	4,7	2,7	3,2

11. Вычислить двойной интеграл , гдеD– область, ограниченная линиями.

12. Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен а. При каких размерах сторон прямоугольника окно будет пропускать наибольшее количество света?