Тесты главы:  1. Математика в экономике 3кр 1руб13.12.2010(N)p с 2012-09-01 по 2012-12-29.     Пройти тест     Результаты теста 

 

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ

АНАЛИЗ

 

1.     Понятие функции.  Способы задания функции.

2.     Классификация функций.

3.     Предел  числовой последовательности.

4.     Бесконечно малые величины и их свойства.

5.     Предел функции.

6.     Основные теоремы о пределах.

7.     Замечательные пределы.

8.     Непрерывность функции.

 

1.    Понятие функции.  Способы задания функции.

Понятие функции является одним из основных понятий современной математики. С этим понятием часто встречаются при изучении реальных процессов в природе, науке и технике. С помощью  различных функций могут быть описаны многие процессы и явления реального мира.

Определение. Переменная величина y называется функцией от переменной величины х, если они связаны между собой так, что каждому рассматриваемому значению величины х соответствует единственное вполне определенное значение величины у.

y=f(x),  y=F(x)-функциональная зависимость х и у.

f, F - характеристики функции,   х - независимая переменная  (аргумент),   у – зависимая переменная.

Совокупность всех значений независимой переменной х, для которых функция определена, называется областью определения или областью существования функции.

Пример: область определения функции

Рассматривают три способа задания функции: аналитический, табличный и графический.

1. Аналитический.

Способ задания функции при помощи формулы называется аналитическим. Этот способ является основным в мат. анализе, но на  практике не удобен.

 

 

 

2. Табличный способ задания функции.

Функцию можно задать с помощью таблицы, содержащей  значения аргумента и соответствующие им значения функции.

3. Графический способ задания функции.

Функция у=f(х) называется заданной графически, если построен ее график. Такой способ задания функции дает возможность определять значения функции только приближенно, так как построение графика и нахождение на нем значений функции сопряжено с погрешностями

 

2.    Классификация функций.

Элементарные функции разделяют на алгебраические и неалгебраические (трансцендентные).

Алгебраической называют функцию, в которой над аргументом производится конечное число алгебраических действий.

К ним относятся:

- целая рациональная функция (многочлен, полином)

- дробно-рациональная функция – отношение двух многочленов

- иррациональная функция (среди действий над аргументом есть ивлечение корня).

К трансцендентным относятся: показательная, логарифмическая, тригонометрические и обратные тригонометрические функции.

 

3.    Предел  числовой последовательности.

Если каждому числу n из натурального ряда чисел 1,2, 3,…, n,.. поставлено в соответствие действительное число х_n, то множество чисел х_{.1  ,} х₂,              …, х_n, … называется числовой последовательностью , числа х_{.1  ,} х ₂,      …, х_n, … называются членами последовательности, х_n – общий членпоследовательности. Обозначается последовательность{х_n }.

Пример. {1/n} означает последовательность:

1, 1/2, 1/3,…, 1/n,…                                    .

Графически последовательность изображается на числовой прямой в виде последовательности точек.

Определение 1. Последовательность {х_n} называется ограниченной сверху (снизу), если существует такое число М (м), что для любого  х_n выполнено неравенство:

х_n ≤  М  ( х_n ≥ м )

Определение 2. Последовательность {х_n} называется ограниченной, если она ограничена и сверху и снизу, т.е.  существуют такие числа  М  и м, что для любого  х_n выполнено неравенство:  м ≤ х_n ≤  М.

Примеры:

1)   1, 2, 3, ……. - ограничена снизу;

2)  -1, -2, -3, ….. - ограничена сверху;

3)   1, 1/2, 1/3, ….. - ограничена

Определение 3. Последовательность {х_n} называется бесконечно большой (б.б.), если

Определение 4. Последовательность {α_n} называется бесконечно малой (б.м.), если 

Теорема 1. Если {х_n} – б.б. последовательность и все ее члены не равны нулю, то последовательность {1/х_n} – б.м. и обратно, если {α_n}- б.м. последовательность и α_n≠ 0, то

{1/α_n}- б.б.

Определение 5. Число а называется пределом последовательности х_n}, если.

Последовательность, имеющая предел, называется сходящейся. Записывается это так:

Замечание 1: Если последовательность {х_n} имеет предел а, то для любого х можно записать:    х_n = а + α_n,          где α_n – б.м.

Замечание 2.   Пусть - любое положительное число, а – некоторое действительное число, тогда множество действительных чисел удовлетворяющих неравенствам      или     называется -окрестностью точки а.

 

 

 -------       х

 

а – центр окрестности,   - радиус окрестности.

Замечание 3.  Всякая б.б. последовательность не имеет предела, т.е..

Замечание 4. Всякая б.м. последовательность является сходящейся и ее предел равен нулю.

 

4.    Бесконечно малые величины и их свойства.

1. Алгебраическая сумма любого конечного числа бесконечно малых есть также величина бесконечно малая.

2. Произведение бесконечно малой на величину ограниченную есть также величина бесконечно малая.

Следствие 1: Произведение бесконечно малой на величину постоянную, есть бесконечно малая.

Следствие 2:  Произведение конечного числа бесконечно малых величин есть бесконечно малая величина.

Следствие 3:  Частное от деления бесконечно малой величины на величину имеющую предел, отличный от нуля, есть также бесконечно малая величина.

Теорема 2.Сумма (разность) двух сходящихся последовательностей есть сходящаяся последовательность, предел которой равен сумме (разности) пределов этих последовательностей.

Теорема 3. Произведение двух сходящихся последовательностей есть сходящаяся последовательность, предел которой равен произведению пределов этих последовательностей.

Теорема 4.  Частное двух сходящихся последовательностей при условии, что предел знаменателя не равен нулю, есть сходящаяся последовательность, предел которой равен частному пределов этих последовательностей.

 

5.    Предел функции.

Определение. Число А называется пределом функции f(x) в точке х=а, если для каждого положительного наперед заданного сколь угодно малого числа >0 найдется такое положительное число, что для всех х, отличных от а и удовлетворяющих неравенству  выполняется неравенство:         .

Число  зависит от , при уменьшении  уменьшается и .

Если А предел f(x) в точке х=а, то обозначают 

Таким образом, когда мы имеем функцию f(x), процесс изменения состоит в том, что значения аргумента приближаются к некоторой точке а, вследствие чего соответствующие значения функции приближаются к своему пределу А.

 

6.    Основные теоремы о пределах.

Теорема 5.  Предел алгебраической суммы конечного числа слагаемых равен сумме пределов этих слагаемых.

Теорема 6.  Предел произведения любого конечного количества сомножителей равен произведению их пределов.

Теорема 7.  Предел частного двух переменных равен частному их пределов, если только предел знаменателя отличен от нуля.

Следствие 1. Постоянный множитель можно выносить за знак предела.

.

Следствие 2 .  Предел степени переменной равен той же степени предела переменной.

.

 

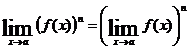Примеры.  Найти предел функции.

 

1) 

2) 

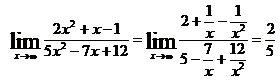
7.    Замечательные пределы.

Теорема. Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен 1.

Этот предел называется первым замечательным пределом.

Пример.

Теорема . Последовательность при , имеет предел,  заключенный между числами 2 и 3.

        где е = 2,71828…

Этот предел называется вторым замечательным пределом.

Число е является основанием логарифмов, которые называются натуральными логарифмами и обозначаются lnx

 

Пример.

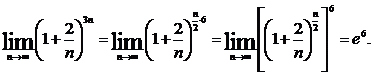
Если обозначить  1/n = α, то второй замечательный предел запишется в виде:

Пример.

 

8.    Непрерывность функции.

Пусть функция y=f(x) определена в точке х=х₀ и ее окрестности. Придадим аргументу новое значение х₁.

Величина  х₁-х₀ называется приращением аргумента.

х₁-х₀=Δх,    х₁=х₀+ Δх

Тогда функция у принимает соответствующее значение f(x₁).:

f(x₁)- f(x₀)= Δу – приращение функции.

f(x₁)= Δу+ f(x₀),         f(x₁)= у₀+Δу

Определение1: Функция y=f(x) называется непрерывной в точке х₀, если бесконечно малому  приращению аргумента соответствует бесконечно малое приращение функции.

Определение 2. Функция y=f(x) называется непрерывной в точке х₀, если:

1.        Эта функция определена при х=х₀.

2.        Предел функции в точке х=х₀ равен значению функции в точке х₀.

Определение 3. Функция  у= f (x) называется непрерывной на отрезке