Матем / 7

 

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

 

1.     Первообразная  функция и неопределенный интеграл.

2.     Свойства неопределенного интеграла.

3.     Таблица  интегралов.

4.   Метод замены переменной.

5.   Метод интегрирования по частям.

6.   Интегрирование рациональных дробей.

7.   Интегрирование тригонометрических функций

 

1. Первообразная  функция и неопределенный интеграл.

Основная задача дифференциального исчисления состоит в нахождении по данной функции ее производной или дифференциала. Многочисленные вопросы науки и техники приводят к постановке обратной задачи: для данной функции f(x) найти такую функцию F(x), производная которой равнялась бы заданной функции f(x), т.е.

F′(x)=f(x)  или  dF(x)= f(x)dx

Определение. Первообразной функцией для данной функции f(x) называется функция F(х), производная которой равна данной функции.

Теорема. Любая непрерывная на сегменте функция имеет на этом сегменте первообразную.

Если функция F(x) – первообразная для функции f(x)  на сегменте a ≤ x ≤ b, то всякая другая первообразная отличается от F(x) на постоянное слагаемое, т.е. может быть представлена в виде F(x)+С, где С – постоянная.

Определение.  Если F(x) – одна из первообразных для функции f(x), то выражение F(x)+C, где С – произвольная постоянная, называетсянеопределенным интегралом.

Неопределенный интеграл обозначается символом

.

f(х) называется подынтегральной функцией, f(x)dx – подынтегральным выражением.

Действие отыскания неопределенного интеграла – нахождение всех первообразных для данной функции, называется интегрированием этой функции.

Операция интегрирования функции является обратной для операции дифференцирования функции.

 

2.    Свойства неопределенного интеграла.

1.        Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.

а)

б)

2.        Неопределенный интеграл от дифференциала функции f(x) равен функции f(x) с точностью до постоянного слагаемого, т.е.

3.        Постоянный множитель в подынтегральном выражении можно выносить за знак неопределенного интеграла, т.е.

4.        Неопределенный интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов этих функций, т.е.

5.        Вид интеграла не меняется при переходе от переменной x к переменной u, где u – дифференцируемая функция от х

Если, то и 

 

3.    Таблица  интегралов.

Для облегчения интегрирования составлена таблица так называемых основных интегралов. Эта таблица получается из основных формул дифференциального исчисления. Справедливость каждой формулы проверяется дифференцированием.

1.                       2. (при n ≠ -1)

3.                     4. 

5.                      6. 

7.            8. 

9.              10. 

11.        12. 

13.

14..

 

4.   Метод замены переменной.

Этот способ интегрирования применяется в случаях, когда преобразования подинтегральной функции с помощью свойств неопределенного интеграла или путем разбиения ее на отдельные слагаемые не приводят к табличным формулам, но такие формулы можно получить в результате перехода к новой переменной. Этот метод интегрирования получил название метода замены переменной или метода интегрирования подстановкой.

Пример.  

 

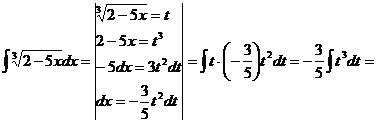
5.   Метод интегрирования по частям.

-       это  формула интегрирования по частям.

Эта формула чаще всего применяется тогда, когда под интегралом имеется произведение алгебраической и трансцендентной функции. При этом за uпринимается функция, которая дифференцированием упрощается, а за dv – та часть подынтегрального выражения, содержащая dx, интеграл от которой известен или может быть найден.

Пример: Найти интеграл  .

,  ,    ,

,    

 

 

Тогда получим:

 

6.   Интегрирование рациональных дробей.

Пусть требуется найти интеграл от дроби, где P(x) и  Q(x) – многочлены, т.е. подинтегральная функция рациональная. Эта дробь называетсяправильной, если степень числителя меньше степени знаменателя. В противном случае дробь называется неправильной.

Любая правильная рациональная дробь может быть представлена в виде суммы конечного числа простейших дробей .

Интегрирование простейших дробей типов

1)   и   2)   выполняется непосредственно:

1) ,

2)  

Пусть знаменатель Q(x) рациональной дроби  разлагается на множители следующим образом:

, где квадратный трехчлен не имеет действительных корней. Тогда имеет место следующая теорема:

Правильную рациональную дробь  можно единственным образом разложить в сумму простейших  дробей:

,

где, ,  , - действительные числа (i=1,2,…)

Одним из наиболее простых методов определения коэффициентов в разложении правильной дроби на простейшие является метод неопределенных коэффициентов.

 

Пример.

= 

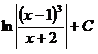
Если знаменатель не имеет действительных корней, то в нем выделяют полный квадрат и производят замену переменной.

При интегрировании неправильной рациональной дроби необходимо выделить целую часть и только потом интегрировать многочлен и правильную дробь.

 

7. Интегрирование тригонометрических функций

Рассмотрим интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.е.

В частных случаях один из показателей (m или n) может равняться нулю.  Пусть m и n – целые неотрицательные числа.

А) Рассмотрим   случай, когда  хотя бы один из показателей m и n есть число  нечетное. В этом случае интеграл  вычисляется методом замены переменной: отделяем от  нечетной степени один множитель и полагаем кофункцию этого множителя равной новой переменной t.

Пример.  

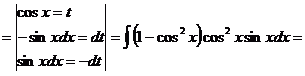
Б) Рассмотрим случай, когда оба показателя m и n – числа четные. В этом случае для вычисления интеграла  используются формулы понижения степени:

,      ,      

В) Рассмотрим  интегралы вида

,  ,   .

Воспользовавшись известными тригонометрическими формулами:

можно преобразовать каждое из произведений под знаком интеграла в алгебраическую сумму и проинтегрировать по табличным формулам.