
Матем / 5
.docx
ПРОИЗВОДНАЯ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ
1. Определение производной.
2. Геометрический и экономический смысл производной.
3. Зависимость между непрерывностью и дифференцируемостью функции.
4. Основные правила дифференцирования.
5. Производная сложной и обратной функции.
6. Таблица производных.
7. Производные высших порядков.
8. Дифференциал функции.
1. Определение производной.
Пусть y=f(x)
непрерывная функция от х. Дадим аргументу
х приращение![]() ,
тогда функция y получит
приращение
,
тогда функция y получит
приращение![]() .
Составим отношение
.
Составим отношение![]() .
Это отношение есть некоторая функция
от
.
Это отношение есть некоторая функция
от![]() .
Может случиться, что эта функция имеет
предел при
.
Может случиться, что эта функция имеет
предел при![]() ,
т.е. существует
,
т.е. существует
![]() .
.
Этот
предел называется производной
от данной функции y и
обычно обозначается через![]() :
:
![]() .
.
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, если этот предел существует и конечен.
Действие нахождения производной называется дифференцированием, а функция, имеющая конечную производную, называется дифференцируемой.
1. Геометрический и экономический смысл
производной.
Геометрический
смысл производной:
для данной функции y=f(x)
ее производная ![]() для
каждого значения х равна угловому
коэффициенту касательной к графику
функции в соответствующей точке.
для
каждого значения х равна угловому
коэффициенту касательной к графику
функции в соответствующей точке.
![]() .
.
Экономический смысл производной.
Пусть
предприятие выпускает однородную
продукцию. Тогда издержки производства y можно
считать функцией количества выпускаемой
продукции x, y=f(x).
Предположим, что количество выпускаемой
продукции изменилось на![]() ,
тогда издержки производства изменяются
на
,
тогда издержки производства изменяются
на![]() :
:![]() .
.
Разделим
приращение издержек производства на
приращение выпускаемой продукции:![]() .
Это равенство выражает среднее приращение
издержек производства на единицу
приращенной продукции, перейдем к
пределy,
.
Это равенство выражает среднее приращение
издержек производства на единицу
приращенной продукции, перейдем к
пределy,
![]() .
.
Этот
предел в экономике называется предельными
издержками производства. Таким
образом, производная ![]() выражает
предельные издержки производства и
характеризует приближенно дополнительные
затраты на производство единицы
дополнительной продукции.
выражает
предельные издержки производства и
характеризует приближенно дополнительные
затраты на производство единицы
дополнительной продукции.
Аналогичным образом могут быть определены предельная выручка, предельный доход, предельный продукт, предельная полезность и другие предельные величины.
3. Зависимость между непрерывностью и дифференцируемостью функции.
Функция y=f(x)
называется непрерывной в
точке, если ![]() .
Функция y=f(x)
называется дифференцируемой в точке,
если она имеет производную, т.е.
.
Функция y=f(x)
называется дифференцируемой в точке,
если она имеет производную, т.е. ![]()
Между этими понятиями существует связь.
Теорема: Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна. Обратное утверждение неверно: непрерывная функция может не иметь производной.
Следствие: Если функция не является непрерывной в некоторой точке, то она не имеет производной в этой точке.
4. Основные правила дифференцирования.
1. Производная постоянной величины равна 0.
![]()
2. Производная алгебраической суммы нескольких дифференцируемых функций равна сумме производных этих функций.
![]()
3. Производная произведения двух дифференцируемых функций равна сумме произведения каждой функции на производную другой функции.
![]()
Следствия:
а) Постоянный множитель можно выносить за знак производной.
![]()
б) Производная произведения любого числа дифференцируемых функций равна сумме произведения производной каждой функции на произведение всех остальных функций.
![]() ;
; ![]()
4. Производная частного равна производной числителя, умноженной на знаменатель, минус производная знаменателя, умноженная на числитель, и все это деленное на квадрат знаменателя.
![]()
Следствия: 1)![]() ;
2)
;
2) ![]() .
.
5. Производная сложной и обратной функции.
1. Производная сложной функции равна произведению производных от функций, составляющих данную функцию.
![]() ,
, ![]() -
дифференцируемые функции. Тогда
-
дифференцируемые функции. Тогда
![]() .
.
2. Производная
обратной функции.
Пусть нам дана дифференцируемая
функция y= f(x).
Если y рассматривать
как аргумент, а x-
функцию, то новая функция ![]() называется
обратной по отношению к y.
Зная производную функции y= f(x)
называется
обратной по отношению к y.
Зная производную функции y= f(x) ![]() ,
можно найти производную обратной
функции
,
можно найти производную обратной
функции![]() ,
предполагая, что обратная функция
существует и непрерывна.
,
предполагая, что обратная функция
существует и непрерывна.
Теорема. Для
дифференцируемой функции с производной
не равной 0, производная обратной функции
равна обратной величине производной
данной функции ![]() .
.
6. Таблица производных.
№
Функция y
Производная ![]()
1 ![]() 0
0
2 ![]() 1
1
3 ![]()
![]()
4 ![]()
![]()
5 ![]()
![]()
6 ![]()
![]()
7 ![]()
![]()
8 ![]()
![]()
9 ![]()
![]()
10 ![]()
![]()
11 ![]()
![]()
12 ![]()
![]()
13 ![]()
![]()
14 ![]()
![]()
15 ![]()
![]()
16 ![]()
![]()
Примеры: Найти производную функций:
а) ![]()
Воспользуемся
формулами ![]() а
также свойством производной, что
постоянный множитель можно выносить
за знак производной.
а
также свойством производной, что
постоянный множитель можно выносить
за знак производной.
![]()
![]()
![]() .
.
б) ![]()
Это
сложная степенная функция.
Обозначим![]() ,
тогда
,
тогда![]() .
Воспользуемся производной сложной
функции.
.
Воспользуемся производной сложной
функции.
![]()
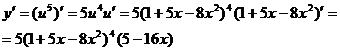
7 . Производные высших порядков.
Производная у′ =f ′(x) называется производной первого порядка. Если f ′(x) дифференцируема, то ее производная обозначается символом у″ =f ″(x)и называется производной второго порядка.
Производная от производной первого порядка называется производной второго порядка.
Если![]() ,
то вторая производная обозначается
,
то вторая производная обозначается
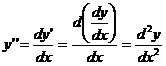 .
.
Производная n-го порядка есть производная от производной (n-1) порядка.
![]()
8. Дифференциал функции.
Пусть
функция y=f(x) дифференцируема
при некотором значении х. Следовательно,
в точке х существует конечная
производная ![]() По
определению предела имеем
По
определению предела имеем ![]()
Отсюда
находим ![]() .
.
y′
от ![]() не
зависит, она остается постоянной при
не
зависит, она остается постоянной при ![]()
Если ![]() то
то ![]() -
является бесконечно малой величиной
того же порядка малости, что и
-
является бесконечно малой величиной
того же порядка малости, что и![]() .
. ![]() -
бесконечно малая величина более
высокого порядка малости, чем первое
слагаемое. Поэтому величину
-
бесконечно малая величина более
высокого порядка малости, чем первое
слагаемое. Поэтому величину ![]() (
(![]() )
называют главной, линейной
относительно
)
называют главной, линейной
относительно ![]() частью
приращения функции; чем меньше
частью
приращения функции; чем меньше![]() ,
тем большую долю приращения составляет
это выражение. Поэтому при малых
значениях
,
тем большую долю приращения составляет
это выражение. Поэтому при малых
значениях ![]() приращение
функции можно заменить
приращение
функции можно заменить![]() ,
т.е.
,
т.е.
![]()
Эту
главную часть приращения функции
называют дифференциалом
функции в
точке х и
обозначают dy или df(x),
следовательно,![]() или
или ![]()
Дифференциал равен произведению ее производной на приращение независимой переменной.
Если f(x)=x, тогда dx=x′![]() =
=![]() , т.е.
, т.е. ![]() .
.
Окончательно
можно записать: ![]()
Из
изложенного выше следует, что![]() ,
т.е. приращение функции
,
т.е. приращение функции ![]() отличается
от дифференциала
отличается
от дифференциала ![]() на
бесконечно малую величину более высокого
порядка, чем
на
бесконечно малую величину более высокого
порядка, чем![]() .
Поэтому при достаточно малых
значениях
.
Поэтому при достаточно малых
значениях ![]() имеем
имеем![]() ,
т.е.
,
т.е.![]() ,
откуда получаем формулу:
,
откуда получаем формулу:
![]() .
.
Чем
меньше значение![]() ,
тем точнее эта формула, и ее можно
использовать для приближенных вычислений.
,
тем точнее эта формула, и ее можно
использовать для приближенных вычислений.
Пример.
Вычислить ![]()
Решение:![]() ,
,
где ![]()
Найдем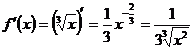 ,
, ![]() .
Тогда имеем:
.
Тогда имеем: ![]()
