32 Уравнения линии в пространстве

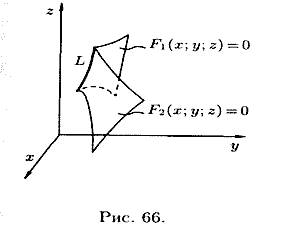
Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 66) или как геометрическое место точек, об­щих двум поверхностям.

Если F₁ ( x_; y;z)  и  F₂ (x; y; z) — уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными:

     

Сравнения системы называются уравнениями линии в пространстве. Например, y=0 

есть уравнения оси Ох. Z=0

.

Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

где и  — произвольные постоянные, причем постоянные и не равны нулю одновременно.

При прямая параллельна оси , при  — параллельна оси .

Вектор с координатами называется нормальным вектором, он перпендикулярен прямой.

При прямая проходит через начало координат.

Также уравнение можно переписать в виде

Направляющий вектор произвольной прямой в дальнейшем обозначается буквой , его координаты - буквами l, m, n:

.

Если известна одна точка прямой и направляющий вектор , то прямая может быть определена (двумя) уравнениями вида

.

33 Выразим параметр из каждого уравнения системы (4.33):, а затем исключим этот параметр:

(4.34)

Уравнение (4.34) называется каноническим уравнением прямой в пространстве. В этом уравнении коэффициенты не равны нулю одновременно, так как это координаты направляющего вектора прямой.

Уравнение прямой, проходящей через две точки

Нам известно, что каноническое уравнение прямой на плоскости вида задает в прямоугольной системе координат Oxy прямую линию, проходящую через точку и имеющую направляющий вектор .

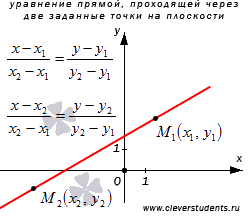
Напишем каноническое уравнение прямой a, проходящей через две заданные точки и .

Очевидно, направляющим вектором прямой a, которая проходит через точки М₁ и М₂, является вектор , он имеет координаты (при необходимости смотрите статьювычисление координат вектора по координатам точек его конца и начала). Таким образом, мы имеем все необходимые данные, чтобы написать каноническое уравнение прямой a – координаты ее направляющего вектора и координаты лежащей на ней точки (и ). Оно имеет вид (или ).

Также мы можем записать параметрические уравнения прямой на плоскости, проходящей через две точки и . Они имеют вид или .

Параметрические уравнения прямой.

, , . (3)

Это - параметрические уравнения прямой, проходящей через точку в направлении вектора . В уравнениях (3) t рассматривается как произвольно изменяющийся параметр, x, y, z - как функции от t; при изменении t величины x, y, z меняются так, что точка M(x; y; z) движется по данной прямой.

Если параметр t рассматривать как переменное время, а уравнения (3) как уравнения движения точки М, то эти уравнения будут определять прямолинейное и равномерное движение точки М. При t=0 точка М совпадает с точкой . Скорость v точки М постоянная и определяется формулой

Приведение общего уравнения к каноническому

Если нужно привести ее уравнения к каноническим или параметрическим . то следует выбрать на этой прямой какую-то точку и найти вектор, параллельный ей. Координатами точки, принадлежащей прямой, является любое из решений заданной линейной системы. Направляющим вектором прямой является вектор

- нормальные векторы плоскостей, задающих прямую. (рис. 10)

34. Угол φ между прямыми K и K' (точнее, один из углов между ними) находится по формуле

где l, m, n и l', m', n'- направляющие коэффициенты прямых Kи K'.

  Пример 

  Найти угол между прямыми

{	2x-2y-z +8=0	{	4x+y+3z-21=0
	x+2y-2z+l=0		2x+2y-3z+15=0

  Решение

  Направляющие коэффициенты первой прямой равны l=2, m=1, n=2. Если за направляющий вектор второй прямой принять векторное произведение {4, 1, 3}х{2, 2, -3}, то направляющие коэффициенты ее равны  -9, 18, 6. Помножив их (чтобы

иметь дело с меньшими числами) на (смотрите замечание),

получим l=-3, m= 6, n=2. Получаем:

 

  Откуда находим,  φ=79⁰.02

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.