9 Вопрос.

Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность)

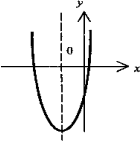Парабола - график функции квадратного трёхчлена у = ах² + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax² + bx +с =0

Функция вида  ( a , b , c , d – некоторые постоянные) называется дробно-линейной . а, b, с, d - постоянные, причем 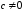(иначе мы имели бы линейную функцию) и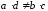(иначе произошло бы сокращение и мы получили бы постоянную функцию).

y=lxl f(x)<=0 для любого x. график симметричен относительно оси ординат

10 Вопрос.

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функцииобычно обозначается, иногда также используется обозначение.

Сложная функция – функция от функции. Если z – функция от у, т.е. z(y), а у, в свою очередь, – функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.

Очень удобно классификацию элементарных функций представить в виде таблицы.

Элементарные функции

• Трансцендентные

• Алгебраические

  • Иррациональные

  • Рациональные

    • Целые рациональные

    • Дробные рациональные

Итак, по приведенной классификации элементарные функции подразделяются наалгебраические и трансцендентные.

Алгебраические функции.

Алгебраическими называют функции, составленные из букв и цифр, соединенных знаками действий сложение, умножение, вычитание, деление, возведение в целую степень и извлечение корня.

Другими словами: алгебраическими называют элементарные функции, которые могут быть получены из двух основных функций f(x)=x и f(x)=1 при помощи любого числа последовательно выполненных алгебраических действий (сложение, умножение, вычитание, деление, возведение в целую степень, извлечение корня) и умножения на числовые коэффициенты.

Например, функция является алгебраической.

Алгебраические функции подразделяются на рациональные и иррациональные.

Рациональные функции.

Рациональными называются алгебраические функции, которые не содержат аргумент под знаком радикала (корня).

Рациональные функции разделяются на целые рациональные функции (многочлены) идробные рациональные (отношение многочленов).

Пример целой рациональной функции: .

Пример дробно-рациональной функции: .

ПРИМЕЧАНИЕ:

Рациональные функции могут содержать и иррациональные коэффициенты (главное, чтобы под знаком радикала не было аргумента функции). Например, - целая рациональная функция, а не иррациональная.

Иррациональные функции.

Иррациональными называются алгебраические функции, содержащие аргумент под знаком радикала (корня).

Примером может являться функция .

Трансцендентные функции.

Трансцендентными называют элементарные функции, которые не являются алгебраическими. (То есть, они образованы при помощи возведения в иррациональную степень, логарифмирования, с использованием тригонометрических и обратных тригонометрических операций).

К примеру, - трансцендентная функция.