Первообразная и неопределенный интеграл. Свойства.
Первообразная. Первообразной функцией для данной функции f(x) на данном промежутке называется такая функция F(x), производная которой равна f(x) или дифференциал которой равен f(x)dx на рассматриваемом промежутке. Любая функция имеет бесчисленное множество первообразных.
Теорема: две различные первообразные одной и той же функции, определенной в некотором промежутке, отличаются друг от друга в этом промежутке на постоянное слагаемое.
Доказательство: пусть F1(x) = f(x) и F2(x) = f(x). Таким образом F1(x) = F2(x). Рассмотрим производную разности
(F1(x) – F2(x)) = F1(x) - F2(x) = 0.
Производная разности двух функций равна нулю, следовательно, эти функции отличаются друг от друга на константу, ч. т. д.
Неопределенный интеграл. Неопределенным интегралом от функции f(x) называется общее выражение для всех первообразных данной непрерывной функции f(x) или от дифференциального выражения f(x)dx. Неопределенный интеграл обоначается
.
Интеграл является функцией общего вида, дифференциал которой равен подынтегральному выражению. Таким образом, можно записать:
.
Свойства неопределенного интеграла:
Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции (следует из определения).
Неопределенный интеграл от дифференциала непрерывной дифференцируемой функции равен самой этой функции с точностью до постоянного слагаемого.
Отличный от нуля постоянный множитель можно выносить за знак интеграла:Af(x)dx = A(F(x)+C) = AF(x) + C1.
Неопределенный интеграл от алгебраической суммы конечного числа функций равен такой же алгебраической сумме интегралов этих функций:
f(x)dx + g(x)dx = (F(x) + C1) + (G(x) + C2) = (F(x) + G(x)) + C.
Неопределенный интеграл не зависит от выбора аргумента.
Доказательство: положим u = (x), где (х) – некоторая непрерывно дифференцируемая функция. Рассмотрим интеграл:
f(u)du = f(u)udx. (1)
В таком случае сложная функция F(u) = F((x)) является первообразной для подынтегральной функции интеграла (1). Действительно, в силу независимости дифференциала первого порядка от выбора переменной, получаем:
dF(u) = F(u)du = f(u)du.
И, следовательно,
.
Поэтому
f(u)du = F(u) + C,
где А(г) = а(г)б ч. т. д.
Интегрирование путем замены переменной. Пусть f(x) непрерывна на интервале (а,b) и x = (t) непрерывно дифференцируема на интервале (,), причем функция отображает интервал (,) в интервал (a,b).
На основании свойства независимости неопределенного интеграла от выбора аргумента, и учитывая, что dx = (t)dt, получаем формулу замены переменной в неопределенном интеграле:
f(x)dx = f((t))(t)dt.
Интегрирование по частям. Пусть u и v – непрерывно дифференцируемые функции от x. На основании формулы дифференциала произведения имеем:
d(uv) = udv + vdu;
udv = d(uv) – v(du).
Интегрируем последнее выражение. Получаем:
udv = d(uv) - vdu;
udv = uv - vdu.
Полученная формула называется формулой интегрирования по частям.
Свойства определенного интеграла.
Определенный
интеграл. Обозначим
через
длину наибольшего частичного отрезка
xi
данного разбиения. Определенным
интегралом от
функции f(x)
по отрезку
называется конечный пределI
интегральной суммы ,
если такой предел существует:
В
случае, если такой предел существует,
функция называется интегрируемой на
.
Свойства определенного интеграла.
Из определения определенного интеграла следует а) если a = b, то
;
б) если поменять местами пределы, то определенный интеграл поменяет знак:
Какие бы ни были числа a, b, c, имеет место равенство:
. *)
Доказательство:
допустим сначала, что a
< b
< c.
Так как предел интегральной суммы
не зависит от способа разбиения отрезка
,
то будем разбивать отрезок
так, чтобы точка с была точкой разбиения.
Если, например, с =xm,
то
можно разбить на две суммы:
.
Переходя к пределу при 0, получаем равенство *). Доказательства для других случаев расположения точек а, b, c легко сводятся к рассмотренному случаю с помощью первых двух свойств.
Постоянный множитель можно выносить за знак определенного интеграла.
Доказательство:
для любого разбиения отрезка
и для любого выбора точекi
.
Переходя к пределу при 0, имеем
.
Определенный интеграл от алгебраической суммы функций равен сумме их интегралов. Действительно, для любого разбиения отрезка
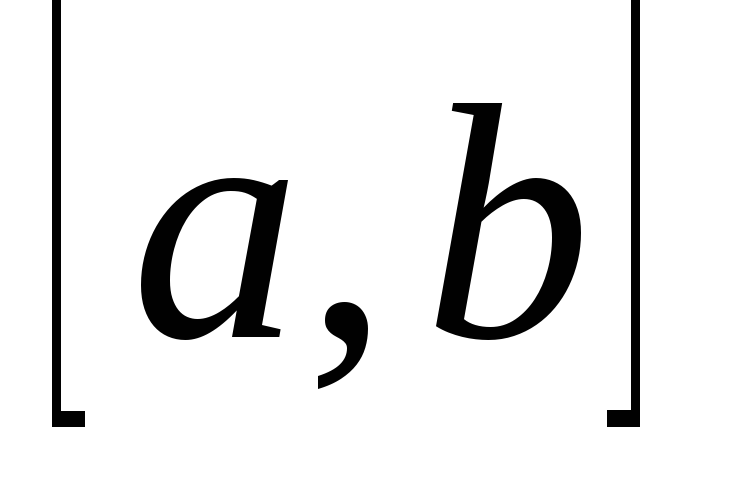и любого выбора точекi:
Замечание: свойство №4 имеет место для любого конечного числа слагаемых.
Если всюду на отрезке
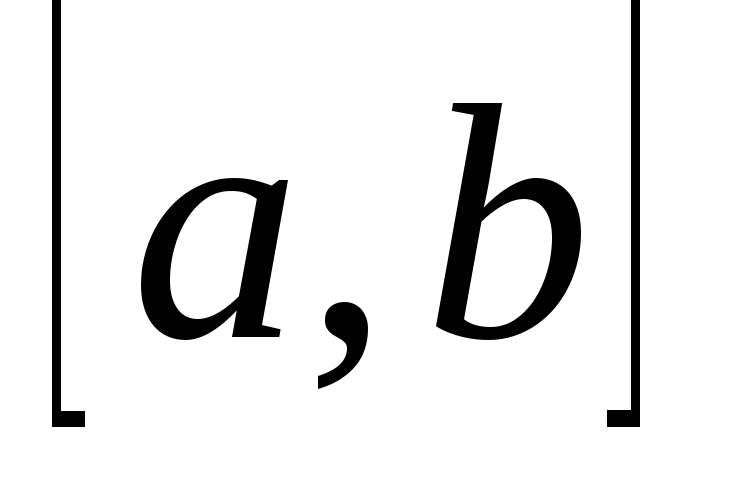функцияf(x)
0, то
.
Доказательство: в
самом деле любая интегральная сумма
для функции f(x)
0 на отрезке
неотрицательна, т.к.f(i)
0, xi
= xi
– xi-1
> 0, i
= 1, 2, …, n.
Переходя к пределу при
0 в неравенстве
,
получаем:
.
6. Если всюду на
отрезке
f(x)
g(x),
то
.
Согласно свойству №5 для функции f(x) – g(x):
.
Но согласно свойству №4:
.
Таким образом,
получаем неравенство
Определенный интеграл, его геометрический смысл.
Определенный
интеграл. Обозначим
через
длину наибольшего частичного отрезка
xi
данного разбиения. Определенным
интегралом от
функции f(x)
по отрезку
называется конечный пределI
интегральной суммы ,
если такой предел существует:
В случае, если такой
предел существует, функция называется
интегрируемой на
.
геометрический
смысл определенного интеграла: если
,
то
равен площади фигуры, ограниченной
графиком функции, осью абсцисс и прямыми
теорема о среднем. Обобщенная теорема о среднем.
Интегральная теорема о среднем значении
Теорема: если
функция f(x)
непрерывна на отрезке
,
то на этом отрезке существует точкаc
такая, что
Доказательство:
так как функция f(x)
непрерывна на
,
то по второй теореме Вейерштрасса
существуют числаm
и M
такие, что
Применяя 6-е свойство определенных интегралов, запишем
Заметим, что
Отсюда получаем соотношение
Положим
Так как число
заключено между наименьшим и наибольшим
значениями непрерывной функции f(x)
на
,
то по теореме о прохождении непрерывной
функции через любое промежуточное
значение существует точка с
такая, чтоf(c)
= .
Поэтому
Геометрический смысл теоремы состоит в следующем: величина определенного интеграла при f(x) 0 равна площади прямоугольника, имеющего высоту f(c) и основание b – a.
Обобщенная теорема о среднем. Если функции f(x) и (x) непрерывны на отрезке
[a, b], и функция (х) знакопостоянна на нем, то на этом отрезке существует точка
, такая, что
Замена переменной в определенном интеграле.
Теорема: пусть f(x)
– непрерывная функция на отрезке
,
функция х =(t)
непрерывно дифференцируема на
,()
= а и ()
= b.
Тогда справедлива формула
Доказательство: По формуле Ньютона-Лейбница
где F(x)
– какая-нибудь первообразная для функции
f(x)
на
.
Рассмотрим на отрезке
сложную функцию от переменнойt:
Ф(t)
= F((t)).
Согласно правилу дифференцирования
сложной функции находим:
Ф(t) = F((t))(t) = f((t))(t).
Отсюда следует,
что функция Ф(t)
является первообразной для функции
f((t))(t),
непрерывной на
.
Поэтому, согласно формуле Ньютона-Лейбница
получаем:
Интегрирование по частям в определенном интеграле.
Теорема: если
функции u(x)
и v(x)
имеют непрерывные производные на отрезке
,
то справедлива формула
Доказательство: так как функция u(x)v(x) является первообразной для функции (u(x)v(x)) = u(x)v(x) + v(x)u(x), то по формуле Ньютона-Лейбница
Используем теперь свойство интеграла суммы. Получим:
или, что то же самое,
Определенный интеграл с переменным верхним пределом.
Определенный интеграл с переменным верхним пределом. Определенный интеграл с переменным верхним пределом является функцией от этого верхнего предела:
Теорема Барроу: производная от интеграла от непрерывной функции по переменному верхнему пределу существует и равна значению подынтегральной функции в точке, равной верхнему пределу, т.е.
Доказательство:
возьмем любое значение х
и дадим ему приращениех
0 такое, чтобы х
.
Тогда функция Ф(х) получит новое значение:
Согласно свойству №2 определенных интегралов имеем
Отсюда находим приращение функции Ф(х):
Применим теперь интегральную теорему о среднем. Получим:
Ф(х + х) – Ф(х) = f(c)x,
где с – число, заключенное между х и х + х. Разделим обе части равенства на х:
Если теперь х
0, то с
х, и тогда, в силу непрерывности функции
f(x)
на
,f(c)
f(x).
Поэтому, переходя к пределу при х
0, получаем:
Таким образом любая непрерывная на отрезке функция f(x) имеет на этом отрезке первообразные, причем функция Ф(х) – интеграл с переменным верхним пределом – является первообразной для f(x). А так как всякая другая первообразная для функции f(x) может отличаться от Ф(х) только на постоянную, то установлена связь между неопределенным и определенным интегралами в виде
Формула
Ньютона-Лейбница.
Таким
образом, функция, непрерывная на отрезке
,
имеет на этом отрезке первообразные,
причем одной из них является функция
Пусть F(x)
– любая другая первообразная для функции
f(x)
на том же отрезке
.
Так как первообразные Ф(х) иF(х)
отличаются на постоянную, то имеет место
равенство
где С – некоторое число. Подставляем в эту формулу значение x = a, получаем
т.е. для любого х
Полагая x = b, получаем формулу Ньютона-Лейбница:
ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ, специальная функция, определяемая интегралом
Этот интеграл не выражается в конечной форме через элементарные функции. Ecли х > 1, то интеграл понимается в смысле главного значения
И. л. введён в матем.
анализ Л. Эйлером в 1768. И. л. Н(х) связан
с интегральной показательной функцией
Ei(x) соотношением li(х) = Ei(lnx). Для больших
положительных х функция li(x) растёт как
ИНТЕГРАЛЬНЫЙ СИНУС И ИНТЕГРАЛЬНЫЙ КОСИНУС -специальные функции, определяемые соответственно интегралами
Эти функции введены итал. математиком Л. Маскерони в 1790. Однако ещё Л. Эйлеру (1781) было известно, что
Этот интеграл является простейшим примером сходящегося, но не абсолютно сходящегося несобственного интеграла. Функции Si(x) и Ci(x) встречаются в различных вопросах анализа и техники, и для них имеются подробные таблицы
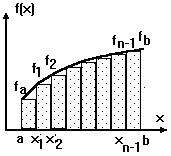
Формула прямоугольников
Если известны значения функции f(x) в некоторых точках x0, x1, … , xm, то в качестве функции “близкой” к f(x) можно взять многочлен Р(х) степени не выше m, значения которого в выбранных точках равны значениям функции f(x) в этих точках.
Если разбить отрезок
интегрирования на n
равных частей
.
При
этом: y0 = f(x0), y1 = f(x1), …. , yn = f(xn).
Составим суммы: y0x + y1x + … + yn-1x
y1x + y2x + … + ynx
Это соответственно нижняя и верхняя интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной
Тогда
или
любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется общей формулой прямоугольников.
Для метода прямоугольников приведены две расчетные формулы, так как площадь прямоугольника на каждом шаге интегрирования может определяться по левой или правой стороне. Суть метода прямоугольников для отрезка [a,b] проиллюстрирована на рисунке, при этом площадь под кривой f(x) (вспомните геометрический смысл определенного интеграла) заменена суммой площадей заштрихованных прямоугольников
Формула трапеций.
Эта формула является более точной по сравнению с формулой прямоугольников.
Подинтегральная функция в этом случае заменяется на вписанную ломаную.
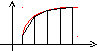
y1 у2 уn
a x1 x2 b x
Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций. Очевидно, что чем больше взять точек n разбиения интервала, тем с большей точностью будет вычислен интеграл.
Площади вписанных трапеций вычисляются по формулам:
После приведения подобных слагаемых получаем формулу трапеций:
Несобственные интегралы по неограниченному промежутку. Теорема сравнения.
Пусть
функция
интегрируема
для всех
и
.
Если существуетпредел
,
то этот предел называют несобственным
интегралом по неограниченному промежутку
и обозначают его
.
Если предел конечен, то говорят, что
несобственный интеграл сходится и его
значение вычисляют по формуле
.
Аналогично определен интеграл
для
интегрируемой при
функции
и
интеграл
для функции , интегрируемой на
.
Если рассмотренные пределы бесконечны,
то говорят, что соответствующий
несобственный интеграл расходится.
Интегралы Эйлера. Гамма функция, свойства.
Г(p)=
Область существования Г – функций.
-
сходящийся
–1
род
=>
=> 
Непрерывность
Г-функция
сходящийся (по признаку Вейерштрасса)
=> равномерная сходимость по параметру, => подынтегральная функция непрерывна, => интеграл сходится к непрерывной функции,
=> Г-функция непрерывна
Дифференцируемость г- функций
Г-функция бесконечное число раз дифференцируема, производные могут быть найдены внесением дифференцирования под знак интеграла.
Функция-оригинал ~ Преобразование Лапласа ~ Основные свойства преобразования Лапласа
Операционное
исчисление - один из наиболее эффективных
методов интегрирования линейных
дифференциальных уравнений с постоянными
коэффициентами. При решении операционным
методом задача интегрирования линейного
дифференциального уравнения с постоянными
коэффициентами с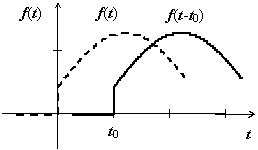
водится
к задаче о решении алгебраического
уравнения.
Функцией-оригиналом
называется
функция f (x)
для которой справедливо:
f (x)
непрерывна при неотрицательных x,
за исключением, быть может конечного
числа точек, f (x) = 0 при x<0,
существуют такие постоянные M
и a,
что
при
всех неотрицательныхx.
Преобразованием
Лапласа
функции f (x)
называется функция
Функция F (p) называется изображением функции f (x), а функция f (x) - оригиналом для F (p).
ПРИМЕР 1. Отыскание изображения и оригинала.
Основные свойства преобразования Лаплалса, используемые при решении дифференциальных уравнений следующие:
оригинал восстанавливется по изображению единственным образом, с точностью до значений в точках разрыва - теорема единственности;
если F (p) и G (p) - изображения соответственно для f (x) и g (x), то изображением для af (x) + bg (x) является aF (p) + bG (p) - линейность преобразования Лапласа;
изображением для производной f (n)(x) является функция pnF(p) - pn-1f (0) - pn-2f '(0) -...- pf (n-2)(0) - f (n-1)(0) - изображение производных;
если F (p) изображения для f (x), то для любого a>0 изображением для f (x-a) является
-
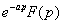теорема запаздывания.
Теорема
запаздывания.
Если f
(t)
F(
p) (т.е. f
(t)
· η(t)
F(
p)), то f
(t
− t0)
· η(t
− t0)
e
−t0
· p
· F(
p) для любого
числа t0
≥ 0.
Док-во.
. Теорема
запаздывания применяется
для изображения функций импульсных,
составных,
периодических.
Рассмотрим этот вопрос подробнее.
Теорема.
(Признак сходимости Даламбера).
Пусть при всех
,
где
.
Тогда ряд сходится. Если же при
,
то ряд расходится.
Доказательство.
Из условий теоремы следует
.
Иными словами,
и
по первой теореме сравнения ряд сходится.
Если
,
то
при
и
ряд расходится.
В предельной форме этот признак выглядит так:
Теорема.
Если существует
,
то при
ряд сходится, при
-
расходится, а при
признак неприменим.
Доказательство.
При
выбираем
так,
чтобы
.
Пусть
выбрано
так, чтобы при
,
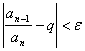т.е.
и
,
.
По предыдущей теореме ряд сходится.
Если же
,
то выберем
так, что
.
Тогда при
и
ряд расходится.
Теорема.
(Признак сходимости Коши).
Пусть
и
при достаточно больших
.
Тогда ряд
сходится.
Если же при
,
то он расходится.
Доказательство.
Неравенство
при
равносильно
неравенству
.
Так как
,
ряд
–
сходится. По теореме 1 из предыдущего
параграфа ряд
также
сходится.
Если же
,
то и
и
равенство
невозможно. Т.о. необходимый признак
сходимости не выполняется и ряд
расходится.
В предельной форме эта теорема выглядит так:
Теорема.
Пусть существует
.
Тогда если
– ряд сходится,
–
ряд расходится,
– признак неприменим.
Доказательство.
Пусть
.
Выберем
так,
чтобы
(т.е.
).
Тогда при
,
т.е.
.
Применяя предыдущую теорему получаем,
что ряд сходится.
Если же
,
то выберем
так,
что
(т.е.
).
Тогда
.
Вновь по предыдущей теореме ряд
расходится.