Параметрически заданные функции

Связь между аргументом и функцией может быть записана через дополнительную переменную, называемую параметром, то есть в виде системы, в которой прописывается зависимость аргумента от параметра и зависимость функции от того же параметра:

, где– это параметр,.

В этом случае функция называетсяфункцией, заданной параметрически.

График функции

Графиком функции y  =  f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.

Другими словами, график функции y = f (х) - это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x).

ОСНОВНЫЕ ЭЛЕМЕНЫ ПОВЕДЕНИЯ ФУНКЦИИ

Функция y=f(x) называется четной, если она удовлетворяет следующим двум условиям:

1. Область определения данной функции должна быть симметрична относительно точки О. То есть если некоторая точка a принадлежит области определения функции, то соответствующая точка -a тоже должна принадлежать области определения заданной функции.

2. Значение функции в точке х, принадлежащей области определения функции должно равняться значению функции в точке -х. То есть для любой точки х, из области определения функции должно выполняться следующее равенство f(x) = f(-x).

Если построить график четной функции, он будет симметричен относительно оси Оу.

Например, тригонометрическая функция y=cos(x) является четной

Функция y=f(x) называется нечетной, если она удовлетворяет следующим двум условиям:

1. Область определения данной функции должна быть симметрична относительно точки О. То есть если некоторая точка a принадлежит области определения функции, то соответствующая точка -a тоже должна принадлежать области определения заданной функции.

2. Для любой точки х, из области определения функции должно выполняться следующее равенство f(x) = -f(x).

График нечетной функции симметричен относительно точки О – начала координат.

Например, тригонометрические функции y=sin(x), y=tg(x), y=ctg(x) являются нечетными.

Функция у=f (х)называется периодической, если существует некоторое число Т !=0 (называемое периодом функции у=f (х) ), такое что при любом значении х, принадлежащем области определения функции, числа х+Т и х-Т также принадлежат области определения функции и выполняется равенство f(x)=f(x+T)=f(x-T).

Следует понимать, что если Т - период функции, то число k*T, где k любое целое число отличное от нуля, также будет являться периодом функции. Исходя из вышесказанного, получаем, что любая периодическая функции имеет бесконечно много периодов. Чаще всего разговор ведется о наименьшем периоде функции.

Тригонометрические функции sin(x) и cos(x) являются периодическими, с наименьшим периодом равным 2*π.

Тригонометрические функции tg(x) и ctg(x) являются периодическими, с наименьшим периодом равным π.

Ограниченность функций

     Функция y=f(x), определенная на множестве X, называется ограниченной сверху, если множество её значений ограниченно сверху. Иначе говоря, функция fограничена сверху, если существует такая постоянная М, что для каждого выполняется неравенство.

 Функция y=f(x), определенная на множестве Х, называется ограниченной снизу, если множество её значений ограниченно снизу, то есть если существует такая постоянная М, что для каждоговыполняется неравенство. Например, таковыми являются показательные функции, функцииy=x²ⁿ, y=x.

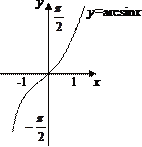
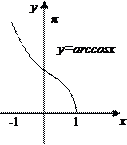
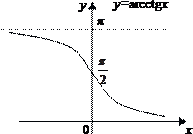
 Функция f(x), определенная на множестве Х, называется ограниченной, если множество её значений ограниченно как сверху, так и снизу. Примерами функций, ограниченных на всей числовой прямой, являются функции y=sin x, y=cos x, y=arccos x, y=arcsin x, y=arctg x, y=arcctg x.

а) если для всех х из некоторого множества Х справедливы неравенства f(x)>M и g(x)<M, где М – некоторое число, то на множестве Х уравнение f(x)=g(x) и неравенство f(x)<g(x) решений не имеют;

б) если для всех х из некоторого множества Х справедливы неравенства f(x) M и g(x)M, где М – некоторое число, то на множестве Х уравнение f(x)=g(x)равносильно системе

 

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.

Действительно, если x₁ < x₂ – корни этого уравнения на промежутке D (f(x)), то f (x₁) = f (x₂) = 0, что противоречит условию монотонности.

Перечислим свойства монотонных функций (предполагается, что все функции определены на некотором промежутке D).

• Сумма нескольких возрастающих функций является возрастающей функцией.

• Произведение неотрицательных возрастающих функций есть возрастающая функция.

• Если функция f возрастает, то функции cf (c > 0) и f + c также возрастают, а функция cf (c < 0) убывает. Здесь c – некоторая константа.

• Если функция f возрастает и сохраняет знак, то функция 1/f убывает.

• Если функция f возрастает и неотрицательна, то где, также возрастает.

• Если функция f возрастает и n – нечетное число, то f ⁿ также возрастает.

• Композиция g (f (x)) возрастающих функций f и g также возрастает.

Основные элементарные функции

Функция	График	Свойства
			-четноеЧетная. Возрастает при. Убывает при.	-нечетноеНечетная. Возрастает при
			-четноеНи четная ни нечетная. Возрастает при	-нечетноеНечетная. Возрастает при
		, Ни четная ни нечетная. Возрастает при, еслиубывает, если.
		, Ни четная ни нечетная. Возрастает, если. Убывает, если
		Четная. Возрастает. Убывает. Периодическая.
		Нечетная. Возрастает . Убывает.. Периодическая.
		.. Нечетная. Возрастает. Периодическая.
		Нечетная. Убывает . Периодическая.
		Нечетная. Возрастает .
		Ни четная ни нечетная. Убывает . .
		Нечетная. Возрастает
		Ни четная, ни нечетная. Убывает .

Определение. Функции, составленные из основных элементарных функций, называются элементарными, если удовлетворяют двум условиям: задаются одним аналитическим выражением в области определения; представляют результат конечного числа алгебраических операций и операций взятия функции от функции.