Раздел II Численные методы

Глава I. Нелинейные уравнения. §1. Уравнения с одним неизвестным.

Наиболее частой задачей, которая встречается на практике, является нахождение корней уравнений с одной неизвестной вида

(1)

Нелинейные уравнения делятся на: - алгебраические,

- трансцендентные.

Алгебраическими называются уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные).

Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.) называются трансцендентными.

Для уравнений, которые невозможно решить простыми методами, используются итерационные методы, т.е. методы последовательных приближений.

Алгоритм нахождения корня нелинейного уравнения с помощью итерационного метода состоит из 2-х этапов:

1. отыскание приближенного значение корня (начального приближения),

2. уточнение значений корней.

Под отысканием начального приближения понимают нахождение какого-либо отрезка оси абсцисс, которому принадлежит один и только один корень этого уравнения.

Аналитические методы отыскания приближенного значения корня основаны на следующих теоремах математического анализа.

Теорема 1

Если функция непрерывна на отрезке, а на концах отрезка имеет разные знаки,то внутрисуществует, по крайней мере, один корень этого уравнения.

Теорема 2

Если функция непрерывна на, на концах интервала имеет разные знаки и ее производнаяв интервалесохраняет знак, то внутри отрезкасуществует единственный корень уравнения (1).

Отыскание начального приближения можно также производить графически, в частности построение графика функции , где значениех перебираются с достаточно малым шагом , позволяет выделить участки числовой оси, где кривая пересекает ось абсцисс.

Другой способ: , например,

к виду:

Итерационный процесс состоит в последовательном уточнении начального приближения . Каждый шаг называетсяитерацией. В результате итераций находится последовательность приближенных значений корня Если эти значения с ростомстремятся к истинному значению корня, то итерационный процесссходится.

§ 2 Метод деления отрезка пополам (метод бисекции).

(1)

Допустим, известен отрезок , где находится корень, т.е.. В качестве начального приближения корняпринимаем середину этого отрезка:

Далее исследуем значение функции на концах отрезкови, т.е. в точках

Отрезок, на концах которого принимает значения разных знаков, содержит искомый корень. Его принимаем в качестве нового отрезкаВторую половину отрезка, где знакне меняется, отбрасываем.

В качестве первого приближения корня принимаем:

Таким образом, к-е приближение вычисляется как (2)

После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после k итераций он сокращается в раз.

Пусть приближенное решение требуется найти с точностью до некоторого заданного малого числа. (3)

Обозначим:

(4)

Из (2) следует, что (4) выполнено, если (5)

Таким образом, итерационный процесс нужно продолжать до тех пор, пока не будет выполнено условие (5).

Пусть для определенности ,(рис). Начальное приближениеТак как в нашем случае, то, отбрасываем.

Р

y

ассматриваем, т.е..

Следующее приближение: .

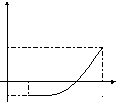
F(b)

a

c₀ c₂

x

c c₁

b

F(a)

Отрезок - отбрасываем, т.к.и

Таким образом ,

Аналогично находим и т.д. до выполнения условия (5).

Итерационный процесс можно завершить и тогда, когда значение функции послек-ой итерации станет меньшим по модулю , т.е.

(6)