20.Три стороны задачи определения напряжений

при выводе формулы опр напр необходимо расм 3 стороны задачи

1) Геометрическая(ГС)

устанавливает закон распределения деформации по сеч бруса

2) Физическая (ФС)

связывает деформации с напр посредством закона Гука

3) Статическая сторона (СС)

связ-ет напр с ВСФ(внутр сил фактор) посредствам зависимостей

21.Простое осевое растяжение – сжатие

ГС

ФС

СС

из (*)и(**)

- ф-ла для определения напряжения раст-сжатии

22.Формула для определения деформации бруса при растяжении-сжатии. Жесткость сечения бруса и физический смысл входящих в формулу величин

Опр-е деформации бруса при раст-сжатии из (**)

l-длина бруса

ЕА-жесткая сечение бруса при растяжении-сжатии

24.Формула для определения угла закручивания круглого бруса. Жесткость сечения бруса и физический смысл входящих в формулу величин

из (**)

25.Кручение брусьев прямоугольного сечения

Wk- αhb^2 -момент сопротивления кручению

Jk- βhb^3 –момент инерции при кручении

для c h\b >10 α≈β≈1\3

т.о. Wk- 1\3 hb^2

26.Кручение тонкостенных стержней открытого и закрытого профиля

Характерной геометрической особенностью тонкостенных стер­жней является то, что их толщина существенно (на порядок и более) меньше других геометрических раз­меров

тонкостенное кольцо закрытого профиля

Характер распре­деления напряжений по толщине тонкостенного стержня открытого профиля близок к равномерному (рис. 4.7, б), а замкнутого профиля меняется по ли­нейному закону, как это показано на рис. 4.7, а. Откуда следует, что напряжения в поперечных сечениях открытого профиля прак­тически не изменятся, если профиль сечения распрямить. Иначе говоря, напряжения в криволинейном открытом профиле будут примерно такими же, как и в прямом.

27.Прямой чистый изгиб

Все элементы конструкции подвергаются изгибу, они все рассчитываются на изгиб. При этом используют расчетную схему конструкции (наиболее распространенная расчетная схема для множества конструкций - балка на двух опорах). Балка – брус, который воспринимает поперечные нагрузки и работает на изгиб.

Допущения при изгибе:

1. плоскость поперечного сечения балки до и после нагружения остается плоской, перпендикулярно.

2. перпендикулярно к оси тела.

3. верхние слои балки растягиваются, а нижние сжимаются. Во всех сечениях балки действуют нормальное напряжение, напряжение сжатия и растяжения.

4. есть слой в поперечном сечении, на котором нормальное напряжение = 0, линейные размеры этого слоя не изменяются.

5. пересечении плоскости в поперечном сечении с нейтральным слоем есть нейтральная линия – центральная ось поперечного сечения.

Чистый изгиб – когда в поперечных сечениях балки действует только изгибающий момент (частный случай).

Поперечный изгиб – когда в поперечных сечениях действует одновременно и изгибающий момент и поперечная сила (общий случай).

Плоский (прямой) изгиб — когда изгибающий момент действует в плоскости, проходящей через одну из главных центральных осей инерции сечения, т.е. все силы лежат в плоскости симметрии балки. Основные гипотезы (допущения): гипотеза о не надавливании продольных волокон: волокна, параллельные оси балки, испытывают деформацию растяжения – сжатия и не оказывают давления друг на друга в поперечном направлении; гипотеза плоских сечений: сечение балки, плоское до деформации, остается плоским и нормальным к искривленной оси балки после деформации. При плоском изгибе в общем случае возникают внутренние силовые факторы: продольная сила N, поперечная сила Q и изгибающий момент М. N>0, если продольная сила растягивающая; при М>0 волокна сверху балки сжимаются, снизу растягиваются. .

Слой, в котором отсутствуют удлинения, называется нейтральным слоем (осью, линией). При N=0 и Q=0, имеем случай чистого изгиба. Нормальные напряжения: , — радиус кривизны нейтрального слоя, y — расстояние от некоторого волокна до нейтрального слоя. Закон Гука при изгибе: , откуда (формула Навье):,J_x — момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости изгибающего момента, EJ_x — жесткость при изгибе, — кривизна нейтрального слоя.

Максимальные напряжения при изгибе возникают в точках, наиболее удаленных от нейтрального слоя: ,J_x/y_max=W_x—момент сопротивления сечения при изгибе, .

Если сечение не имеет горизонтальной оси симметрии, то эпюра нормальных напряжений  не будет симметричной. Нейтральная ось сечения проходит через центр тяжести сечения. Формулы для определения нормального напряжения для чистого изгиба приближенно годятся и когда Q0. Это случай поперечного изгиба. При поперечном изгибе, кроме изгибающего момента М, действует поперечная сила Q и в сечении возникают не только нормальные , но и касательные  напряжения. Касательные напряжения определяются формулой Журавского: , гдеS_x(y) — статический момент относительно нейтральной оси той части площади, которая расположена ниже или выше слоя, отстоящего на расстоянии "y" от нейтральной оси; J_x — момент инерции всего поперечного сечения относительно нейтральной оси, b(y) — ширина сечения в слое, на котором определяются касательные напряжения.

Для прямоугольного сечения: ,F=bh, для круглого сечения:,F=R², для сечения любой формы ,

k— коэфф., зависящий от формы сечения (прямоугольник: k= 1,5; круг - k= 1,33).

M_max и Q_max определяются из эпюр изгибающих моментов и поперечных сил. Для этого балка разрезается на две части и рассматривается одна из них.

Действие отброшенной части заменяется внутренними силовыми факторами М и Q, которые определяются из уравнений равновесия. В некоторых вузах момент М>0 откладывается вниз, т.е. эпюра моментов строится на растянутых волокнах. При Q= 0 имеем экстремум эпюры моментов. Дифференциальные зависимости между М,Q и q:

q — интенсивность распределенной нагрузки [кН/м]

Главные напряжения при поперечном изгибе:

.

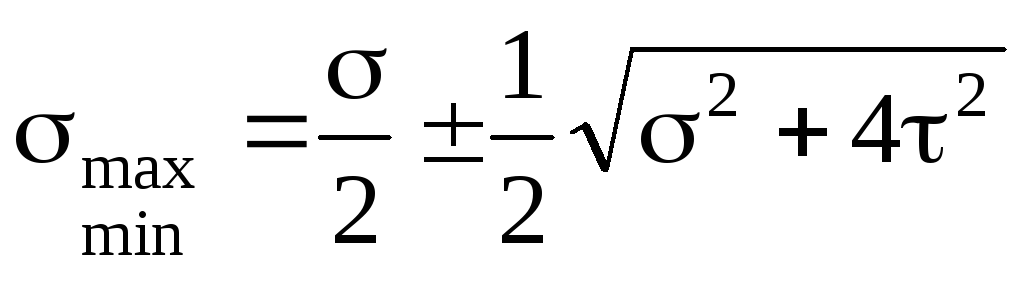из (*)и(**)-формула для вычисления норм напр при прямом чистом изгибе