
- •Федеральное агентство по образованию
- •2. Содержание и структура дисциплины.
- •Тема 4. Системы векторов. N-мерное векторное пространство. Евклидово пространство.
- •Раздел III. Аналитическая геометрия
- •Тема 8. Прямые линии и плоскости.
- •Тема 9. Кривые и поверхности второго порядка.
- •Тема 10. Системы линейных неравенств. Линейные задачи оптимизации.
- •3. Рекомендуемая литература. Основная литература:
- •Дополнительная литература:
- •4. Методические указания по изучению дисциплины.
- •5. Материалы для контроля знаний студентов.
- •Раздел II. Векторная алгебра.
- •Раздел III. Аналитическая геометрия.
- •6. Приложения.
- •6.1. Образец решения контрольных задач типового варианта.
- •, .
- •3А) Находим матрицу , обратную к, методом присоединённой матрицы, по формуле: ,где:
- •6.2. Краткие теоретические сведения.
- •Тема 1. Определители.
- •Тема 2. Матрицы.
- •Тема 3. Системы линейных уравнений. Модель Леонтьева.
- •Тема 4. Системы векторов. N-мерное векторное пространство. Евклидово пространство.
- •Тема 5. Линейные операторы. Собственные числа и векторы.
- •Тема 6. Квадратичные формы.
- •Тема 7. Векторная алгебра.
- •3) ; 4)
- •3) ; 4)5);
- •1) ; 2);
- •Тема 8. Прямые линии и плоскости.
- •Тема 9. Кривые второго порядка.
- •Тема 10. Системы линейных неравенств. Линейные задачи оптимизации.
- •6.3 Образец оформления обложки с контрольной работой.
- •С о д е р ж а н и е
5. Материалы для контроля знаний студентов.
Итоговой формой контроля знаний является экзамен в конце семестра обучения. На экзамене студент должен показать знание теоретических основ курса в объёме вопросов, приведённых в разделе 5.2 и умение решать задачи, подобные тем, что имеются в его контрольной работе.
5.1. Задания для контрольной работы.
1 – 10. Вычислить определитель:
а)
непосредственным
разложением по
![]() строке;
строке;
б)
непосредственным
разложением по
![]() столбцу.
столбцу.
1.
 2.
2. 3.
3.
![]()
![]()
![]()
4.
 5.
5. 6.
6.
![]()
![]()
![]()
7.
 8.
8. 9.
9.
![]()
![]()
![]()
10.

![]()
11
– 20. Найти
матрицу
![]() ,
если
,
если
![]() .
.
11.![]() ,
,![]() 12.
12.![]() ,
,![]()
13.![]() ,
,![]() 14.
14.![]() ,
,![]()
15.![]() ,
,![]() 16.
16.![]() ,
,![]()
17.![]() ,
,![]() 18.
18.![]() ,
,![]()
19.![]() ,
,![]() 20.
20.![]() ,
,![]() .
.
21
– 30. Найти
собственные
числа и собственные векторы матрицы
![]() .
.
21.
![]() .
22.
.
22.![]() .
23.
.
23.![]() .
.
24.
![]() .
25.
.
25.![]() .
26.
.
26.![]() .
.
27.
![]() .
28.
.
28.![]() .
29.
.
29.![]() .
.
30.
![]() .
.
31 – 40.Дана система трех линейных уравнений с тремя неизвестными. Требуется: а) найти решение системы методом Крамера;
б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса.
31.
 32.
32.
33.
 34.
34.
35.
 36.
36.
37.
 38.
38.
39.
 40.
40.
41–50. Найти общее решение для каждой из данных систем методом Гаусса:
41
а) б)
б)
42
а) б)
б)
43.
а) б)
б)
44.
а) б)
б)
45.
а) б)
б)
46.
а) б)
б)
47.
а) б)
б)
48.
а) б)
б)
49.
а) б)
б)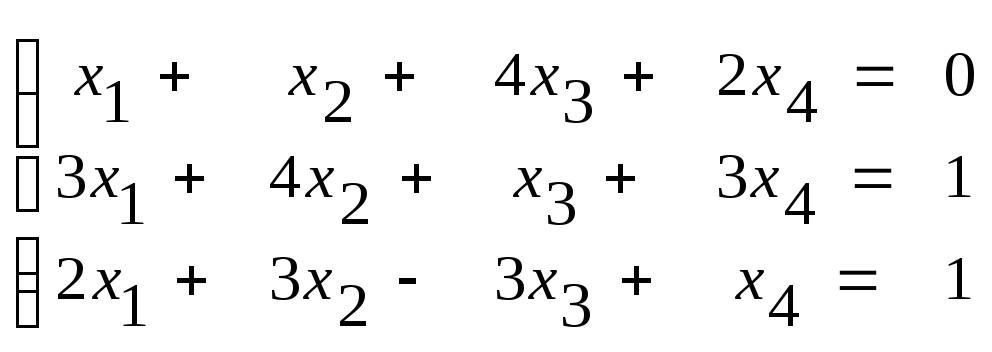
50.
а) б)
б)
51 – 60. Исследовать квадратичную форму на знакоопределённость (по критерию Сильвестра).
51.
![]() .
.
52.
![]() .
.
53.
![]() .
.
54.
![]() .
.
55.
![]() .
.
56.
![]() .
.
57.
![]() .
.
58.
![]() .
.
59.
![]() .
.
60.
![]() .
.
61
– 70. Даны
векторы
![]() .
Требуется:
.
Требуется:
а)
вычислить
скалярное произведение векторов
![]() ,
если
,
если
![]() ,
,![]() ;
б)вычислить
векторное произведение векторов
;
б)вычислить
векторное произведение векторов
![]() ;в)
показать,
что векторы
;в)
показать,
что векторы
![]() образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора![]() в этом базисе.
в этом базисе.
61.
![]()
62.
![]()
63.
![]()
64.
![]()
65.
![]()
66.
![]()
67.
![]()
68.
![]()
69.
![]()
70.
![]()
71-80.
Даны вершины
треугольника
![]() .Требуется
найти:
.Требуется
найти:
а)
длину стороны
![]() ;
б) уравнение
стороны
;
б) уравнение
стороны
![]() ;
;
в)
уравнение
медианы
![]() ,проведённой
из вершины
,проведённой
из вершины
![]() ;
;
г)
уравнение
высоты
![]() ,
проведённой из вершины
,
проведённой из вершины
![]() ;
;
д)
длину
![]() высоты
высоты
![]() ;
е)площадь
;
е)площадь
![]() треугольника
треугольника
![]() .Сделать
чертёж.
.Сделать
чертёж.
71.
![]() .
72.
.
72.
![]()
73.
![]() 74.
74.
![]()
75.
![]() 76.
76.
![]()
77.
![]() 78.
78.
![]()
79.
![]() 80.
80.
![]()
81
– 90. Даны
вершины пирамиды
![]() .Требуется
найти:
.Требуется
найти:
а)
длины ребер
![]() и
и![]() ;
б) угол
между ребрами
;
б) угол
между ребрами
![]() и
и![]() ;
;
в)
площадь
грани
![]() ;
г)объем
пирамиды
;
г)объем
пирамиды
![]() ;
;
д)
уравнение
плоскости грани
![]() ;
;
е)
длину
![]() высоты
высоты![]() пирамиды
пирамиды
![]() .
.
81.
![]()
82.
![]()
83.
![]()
84.
![]()
85.
![]()
86.
![]()
87.
![]()
88.
![]()
89.
![]()
90.
![]()
91–100. Установить, какую невырожденную кривую определяет алгебраическое уравнение второго порядка, построить её.
91.
![]() 92.
92.
![]()
93.
![]() 94.
94.
![]()
95.
![]() 96.
96.
![]()
97.
![]() 98.
98.
![]()
99.
![]() 100.
100.
![]()
101-110. Требуется: а) изобразить графически область допустимых решений системы неравенств; б) найти графическим способом решение задачи линейного программирования.
101.
 102.
102. 103.
103.
104.
 105.
105. 106.
106.
107.
 108.
108.
109.
 110.
110.
111-120.
Имеются
данные о работе трёх отраслей экономики
в отчётном периоде и план выпуска
конечной продукции
![]() в следующем периоде (в усл. ден. ед.).
Требуется, используя модель Леонтьева
многоотраслевой экономики, найти:а)
матрицы коэффициентов прямых и полных
затрат; б)
плановые объёмы выпуска валовой продукции
каждой из отраслей, межотраслевые
поставки и объёмы выпуска чистой
продукции. В ответе записать данные
межотраслевого баланса планового
периода. (Указание:
значения
коэффициентов прямых и полных затрат
вычислить с точностью до 0.01; значения
плановых объёмов выпуска валовой и
чистой продукции, межотраслевых поставок
округлить до целых значений).
в следующем периоде (в усл. ден. ед.).
Требуется, используя модель Леонтьева
многоотраслевой экономики, найти:а)
матрицы коэффициентов прямых и полных
затрат; б)
плановые объёмы выпуска валовой продукции
каждой из отраслей, межотраслевые
поставки и объёмы выпуска чистой
продукции. В ответе записать данные
межотраслевого баланса планового
периода. (Указание:
значения
коэффициентов прямых и полных затрат
вычислить с точностью до 0.01; значения
плановых объёмов выпуска валовой и
чистой продукции, межотраслевых поставок
округлить до целых значений).
111.
|
Отрасли производства |
Отрасти потребления |
Конечный продукт |
Валовой продукт | ||
|
I |
II |
III | |||
|
I |
10 |
20 |
10 |
60 |
100 |
|
II |
20 |
30 |
20 |
30 |
100 |
|
III |
60 |
10 |
20 |
10 |
100 |
|
Чистый продукт |
10 |
40 |
50 |
|
|
|
Валовой продукт |
100 |
100 |
100 |
|
|
112.
|
Отрасли производства |
Отрасти потребления |
Конечный продукт |
Валовой продукт | ||
|
I |
II |
III | |||
|
I |
20 |
20 |
25 |
35 |
100 |
|
II |
50 |
10 |
10 |
30 |
100 |
|
III |
15 |
20 |
40 |
25 |
100 |
|
Чистый продукт |
15 |
50 |
25 |
|
|
|
Валовой продукт |
100 |
100 |
100 |
|
|
113.
|
Отрасли производства |
Отрасти потребления |
Конечный продукт |
Валовой продукт | ||
|
I |
II |
III | |||
|
I |
10 |
40 |
10 |
40 |
100 |
|
II |
10 |
20 |
40 |
30 |
100 |
|
III |
20 |
30 |
30 |
20 |
100 |
|
Чистый продукт |
60 |
10 |
20 |
|
|
|
Валовой продукт |
100 |
100 |
100 |
|
|
114.
|
Отрасли производства |
Отрасти потребления |
Конечный продукт |
Валовой продукт | ||
|
I |
II |
III | |||
|
I |
10 |
40 |
20 |
30 |
100 |
|
II |
50 |
20 |
25 |
5 |
100 |
|
III |
30 |
20 |
20 |
30 |
100 |
|
Чистый продукт |
10 |
20 |
35 |
|
|
|
Валовой продукт |
100 |
100 |
100 |
|
|
115.
|
Отрасли производства |
Отрасти потребления |
Конечный продукт |
Валовой продукт | ||
|
I |
II |
III | |||
|
I |
10 |
40 |
30 |
20 |
100 |
|
II |
40 |
30 |
20 |
10 |
100 |
|
III |
30 |
20 |
40 |
10 |
100 |
|
Чистый продукт |
20 |
10 |
10 |
|
|
|
Валовой продукт |
100 |
100 |
100 |
|
|
116.
|
Отрасли производства |
Отрасти потребления |
Конечный продукт |
Валовой продукт | ||
|
I |
II |
III | |||
|
I |
15 |
25 |
30 |
30 |
100 |
|
II |
10 |
40 |
20 |
30 |
100 |
|
III |
30 |
30 |
30 |
10 |
100 |
|
Чистый продукт |
45 |
5 |
20 |
|
|
|
Валовой продукт |
100 |
100 |
100 |
|
|
117.
|
Отрасли производства |
Отрасти потребления |
Конечный продукт |
Валовой продукт | ||
|
I |
II |
III | |||
|
I |
15 |
15 |
25 |
45 |
100 |
|
II |
15 |
20 |
30 |
35 |
100 |
|
III |
10 |
25 |
20 |
45 |
100 |
|
Чистый продукт |
60 |
40 |
25 |
|
|
|
Валовой продукт |
100 |
100 |
100 |
|
|
118.
|
Отрасли производства |
Отрасти потребления |
Конечный продукт |
Валовой продукт | ||
|
I |
II |
III | |||
|
I |
10 |
20 |
20 |
50 |
100 |
|
II |
20 |
25 |
25 |
30 |
100 |
|
III |
25 |
25 |
30 |
20 |
100 |
|
Чистый продукт |
45 |
30 |
25 |
|
|
|
Валовой продукт |
100 |
100 |
100 |
|
|
119.
|
Отрасли производства |
Отрасти потребления |
Конечный продукт |
Валовой продукт | ||
|
I |
II |
III | |||
|
I |
25 |
10 |
20 |
45 |
100 |
|
II |
25 |
20 |
50 |
5 |
100 |
|
III |
10 |
30 |
20 |
40 |
100 |
|
Чистый продукт |
40 |
40 |
10 |
|
|
|
Валовой продукт |
100 |
100 |
100 |
|
|
120.
|
Отрасли производства |
Отрасти потребления |
Конечный продукт |
Валовой продукт | ||
|
I |
II |
III | |||
|
I |
15 |
20 |
30 |
35 |
100 |
|
II |
30 |
15 |
20 |
35 |
100 |
|
III |
10 |
20 |
30 |
40 |
100 |
|
Чистый продукт |
45 |
45 |
20 |
|
|
|
Валовой продукт |
100 |
100 |
100 |
|
|
5.2. Вопросы к экзамену.
Раздел I. Линейная алгебра.
Понятие матрицы. Частные виды матриц (квадратная, треугольная, диагональная, нулевая, единичная). Элементарные преобразования матриц. Понятие эквивалентности и равенства матриц.
Действия над матрицами (сложение, вычитание, умножение матрицы на число, умножение матрицы на матрицу) и их свойства. Линейная комбинация матриц.
Определители 2-ого и 3-егопорядка, их вычисление. Основные свойства определителей.
Понятие определителя n-ого порядка. Минор и алгебраическое дополнение элемента определителя. Теорема о разложении определителя по элементам строки или столбца.
Понятие системы линейных уравнений (СЛУ). Частные виды СЛУ (квадратная, однородная, неоднородная). Матрица, расширенная матрица, определитель СЛУ.
Решение, множество решений, совместность, несовместность, определённость, неопределённость, эквивалентность СЛУ. Элементарные преобразования СЛУ, их основное свойство.
Теорема Крамера (о разрешимости СЛУ порядка
 ).
Формулы Крамера для решения СЛУ, условия
их применимости.
).
Формулы Крамера для решения СЛУ, условия
их применимости.Метод Гаусса решения СЛУ, условия его применимости. Условия несовместности, определённости и неопределённости СЛУ по методу Гаусса.
Преобразования СЛУ, выполняемые при выполнении прямого и обратного ходов метода Гаусса. Базисные и свободные переменные. Нахождение общего решения СЛУ. Частные решения СЛУ.
Понятие обратной матрицы. Вырожденные и невырожденные матрицы. Теорема о существовании обратной матрицы. Основные способы нахождения обратной матрицы.
Матричные уравнения и их решение. Матричная форма записи СЛУ. Матричный способ (метод обратной матрицы) решения СЛУ и условия его применимости.
Однородные СЛУ, условия существования их ненулевых решений. Свойства частных решений однородных СЛУ.
Минор
 -ого
порядка, базисный минор, ранг матрицы.
Вычисление ранга матрицы. Критерий
совместности СЛУ (теорема Кронеккера-Капелли).
-ого
порядка, базисный минор, ранг матрицы.
Вычисление ранга матрицы. Критерий
совместности СЛУ (теорема Кронеккера-Капелли).Понятие
 -мерного
арифметического вектора. Равенство
векторов. Действия над векторами
(сложение, вычитание, умножение на
число). Линейная комбинация векторов.
-мерного
арифметического вектора. Равенство
векторов. Действия над векторами
(сложение, вычитание, умножение на
число). Линейная комбинация векторов.Скалярное произведение арифметических векторов. Длина вектора и угол между векторами. Понятие ортогональности векторов.
Система векторов и её линейная комбинация. Понятие линейной зависимости и независимости системы векторов. Теорема о необходимом и достаточном условиях линейной зависимости системы векторов.
Понятие векторного пространства
 ,
евклидова пространства
,
евклидова пространства .
Базис, канонический базис, ранг
.
Базис, канонический базис, ранг .
Разложение вектора в
.
Разложение вектора в по векторам его базиса, координаты
вектора. Теорема о единственности
разложения вектора в данном базисе.
по векторам его базиса, координаты
вектора. Теорема о единственности
разложения вектора в данном базисе.Понятие оператора, линейного оператора. Матрица линейного оператора. Сумма (разность) операторов, произведение оператора на число, произведение оператора на оператор, обратный оператор.
Понятие собственного числа и собственного вектора оператора. Характеристическое уравнение. Нахождение собственных чисел и векторов оператора.
Понятие квадратичной формы. Матрица квадратичной формы. Вырожденная, невырожденная, каноническая квадратичная форма. Закон инерции квадратичных форм.
Понятие знакоопределённости квадратичной формы. Главные миноры. Критерии знакоопределённости квадратичной формы.
