21. Методика изучения числовых выражений.

      Понятие математического выражения (или просто выражения), изучаемое в начальных классах, имеет важное значение. Так, это понятие помогает учащимся овладеть вычислительными навыками. Действительно, часто вычислительные ошибки связаны с непониманием структуры выражений, нетвердым знанием порядка выполнения действий в выражениях. Усвоение понятия выражения обуславливает формирование таких важных математических понятий, как равенство, неравенство, уравнение. Умение составлять выражения по задаче необходимо для овладения умения решать задачи алгебраическим способом, т.е. с  помощью составления уравнений.

      С первыми выражениями – суммой и разностью – дети знакомятся при изучении сложения и вычитания  в концентре «Десяток». Не используя  специальных терминов, первоклассники производят вычисления, записывают выражения, читают их, заменяют число суммой, основываясь на наглядных представлениях. При этом выражение 4+3 они читают следующим образом: «к четырем прибавить три» или «4 увеличить на 3». Находя значения выражений, состоящих из трех чисел, которые соединены знаком сложения и вычитания, учащиеся фактически пользуются правилом порядка выполнения действий в неявном виде и выполняют первые тождественные преобразования выражений.

      Познакомившись  с выражениями вида а+в, первоклассники сначала употребляют термин «сумма» для обозначения числа, получающегося в результате сложения, т.е. сумма, трактуется как значение выражения. Затем с появлением более сложных выражений, например вида (а+в)-с, появляется необходимость иного понимания термина «сумма». Выражение а+в называется суммой, а его компоненты – слагаемыми. При введении выражений вида а-в, а·в, а:в поступают аналогично. Сначала разностью (произведением, частным) называют значение выражения, а затем само выражение. Одновременно учащимся сообщают названия его компонентов: уменьшаемое, вычитаемое, множители, делимое и делитель. Например, в равенстве 9-4=5   9-уменьшаемое, 4-вычитаемое, 5-разность. Запись 9-4 также называется разностью. Можно вводить эти термины в другой последовательности: предложить учащимся записать пример 9-4, пояснив, что записана разность, и вычислить, чему равна записанная разность. Учитель вводит название полученного числа: 5- тоже разность. Другие числа при вычитании называются: 9- уменьшаемое, 4- вычитаемое.

      Запоминанию новых терминов способствуют плакаты вида

УМЕНЬШАЕМОЕ                         ВЫЧИТАЕМОЕ                   7                        -                   2                       =           5                                              РАЗНОСТЬ                                        РАЗНОСТЬ                                                                                                               (значение разности)

        

Для закрепления  этих терминов предлагаются упражнения вида : «Вычислите сумму чисел; запишите сумму чисел; сравните суммы чисел (вставьте знак >,< или = вместо · в запись 4 + 3 · 5 + 1   и прочтите полученную запись); замените число суммой одинаковых (разных) чисел; заполните таблицу; составьте по таблице примеры и решите их». Важно, чтобы дети поняли, что при вычислении суммы производится указанное действие (сложение), а при записи суммы получаем два числа, соединенных знаком плюс.

     При изучении сложения и вычитания в  пределах 10 включаются выражения, состоящие  из трех и более чисел, соединенных одинаковыми или различными знаками действий вида: 3+1+1, 4-1-1, 2+2+2+2, 7-4+2, 6+3-7. раскрывая смысл таких выражений, учитель показывает, как их читают (например, к трем прибавить один и к полученному числу прибавить ещё один). Вычисляя значения этих выражений, дети практически овладевают правилом о порядке действий в выражениях без скобок, хотя и не формулируют его. Несколько позднее детей учат прообразовывать выражения в процессе вычислений, например: 10-7+5=3+5=8. такие записи являются первым шагом в выполнении тождественных преобразований. Знакомство  первоклассников с выражениями вида 10- (6+2), (7-4)+5 и т.п. готовит их к изучению правил прибавления числа к сумме, вычитания числа из суммы и др., к записи решения составных задач, а также способствует более глубокому усвоению понятия выражения.

      На  следующем этапе усвоения понятия  выражения учащиеся знакомятся с  выражениями, в которых используются скобки: (10-3)+4,         (6-2)+5. они могут быть введены посредством текстовых задач. Учитель предлагает составить на наборном полотне суммы и разности чисел 10 и 3, используя карточки, на которых записаны эти числа и знаки действий. Затем составленную учениками разность 10-3 учитель заменяет подготовленной заранее карточкой с этой разностью. Следующее задание: составить выражение (на этом этапе учащиеся говорят о нем как о примере),  используя разность, число 4 и знак +. При чтении полученного выражения обращается внимание на то, что его компонентами являются разность и число. «Чтобы было заметно, - говорит учитель,- что разность является слагаемым, её заключают в скобки».

      Самостоятельно  конструируя выражения, дети осознают их структуру, овладевая умением  читать, записывать, вычислять их значения.

      Вводятся  термины «математическое выражение» (или просто «выражение») и «значение выражения». Определения этих терминов не даются. Записав несколько простейших выражений: сумм, разностей, учитель называет их математическими выражениями. Предложив вычислить эти примеры, он объявляет, что числа, полученные в результате вычисления, называются значением выражения. Дальнейшая работа над числовыми выражениями состоит в том, что дети упражняются в чтении, записи под диктовку, составлении выражений, заполнении таблиц, широко используя при этом новые термины.

Правила порядка выполнения действий.

№ п/п	Особенности числового выражения	Порядок выполнения действий	Примеры
1	Содержит только +  и – или только х и :	По порядку (слева  направо)	1    2     3 65 - 20 + 5 - 8 = 42     1   2   3 24 : 4 · 2 : 3 = 4
2	Содержит не только + и - , но и х и :	Сначала выполняют  по порядку (слева направо) х и : , а потом + и – (слева направо)	3     1   2 120 – 20 : 4 · 6 = 90        2      3      1 460 + 40 – 50 · 4 = 300        1   3       4   2 360 : 4 + 10 – 8 · 5 = 60        1    3     2 180 : 2  - 90 : 3 = 60
3	Содержит одну или несколько пар скобок	Сначала находят  значения выражений в скобках, а  затем выполняют действия по правилам 1 и 2	3         1   2 1000- (100 · 9 + 10) =90   3      1     2 5· (76 – 6 + 10) = 400     3         1        2 80+ (360 - 300) ·5 = 380      3     1      4     2 99 · (24-23) –(12-4) =91

Для подсчета значения выражения часто  приходится его преобразовывать, особенно, если выражение содержит большое  количество действий и скобок.

     Преобразование  выражения – это замена данного выражения другим, значение которого равно значению заданного выражения. Преобразования выражений выполняются опираясь на свойства арифметических действий и следствия, вытекающие их них (правила: как прибавить сумму к числу, как вычесть число из суммы, как умножить число на произведение и т.д.).  При изучении каждого правила, учащиеся убеждаются в том, что в выражениях определенного вида можно выполнять действия по-разному, но значение выражения при этом не изменяется.

22. Использование условного обозначения чисел при обучении математике.

Пучки — десятки палочек и отдельные палочки используются для демонстрации образования и десятичного состава двузначных чисел. С этой же целью можно использовать полоски с кружками или треугольниками для иллюстрации десятков (10 полосок по 10 фигур) и единиц (полоски с 1, 2, ... , 9 фигурами). Иногда вместо полосок используют карточки-прямоугольники с изображением числовых фигур (точек) для иллюстрации единиц и карточки-треугольники, изображающие десятки.

Рассматриваются числа, полученные в результате счета десятков и единиц. Вначале можно обратиться к жизненной ситуации. Можно ввести модели десятков и единиц в виде треугольников и отдельных точек. Затем показывают треугольник, заполненный точками (кружками) по такому же «правилу», который будет обозначать десяток. На данном уроке это пособие можно использовать как демонстрационное: дети называют число, которое обозначено треугольниками и отдельными точками, или сами обозначают число с помощью этого пособия. В дальнейшем, когда работать практически с пучками палочек будет трудно, рисунки треугольников и отдельных точек помогут детям хорошо усвоить десятичный состав чисел, при этом треугольники уже не заполняют точками, договариваясь о том, что нарисованные в одну клетку треугольники обозначают десятки, а точки справа от них — единицы. При таком способе детям легко выполнять рисунки в тетрадях:

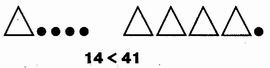
На каждом уроке, отведенном на изучение нумерации, идет работа над задачами. Вначале решаются простые задачи. Это задачи на нахождение суммы и остатка, на увеличение и уменьшение числа на несколько единиц, на разностное сравнение. К задачам дети рисуют «картинки с точками» или работают с фишками, поясняя: мальчиков на 2 больше, чем девочек, значит, берем столько кружков, сколько треугольников, и еще 2; девочек на карусели на 2 меньше, чем мальчиков, значит, их было столько же, сколько мальчиков, но без 2. Схемы к этим задачам выглядят так.

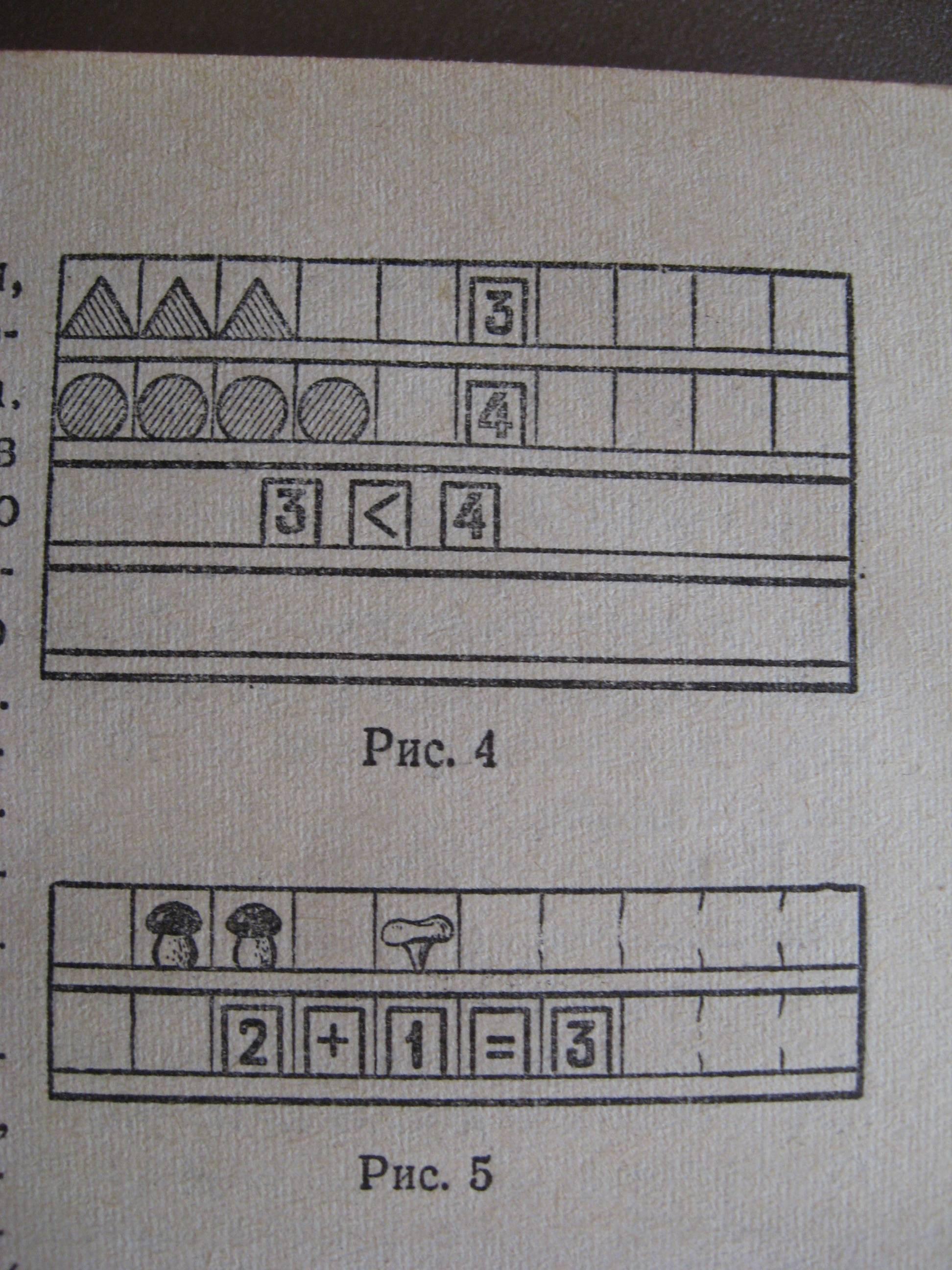
Важное место на уроках в 1-3 классах занимают наборные полотна различной конструкции, изготовляемые из картона, фанеры, ткани. На рисунке 4 изображено демонстрационное наборное полотно, а на рисунке 5 – индивидуальное.